38. Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Дифракция Френеля на простейших преградах.

38. Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Дифракция Френеля на простейших преградах.

 

Явление дифракции света. Принцип Гюйгенса-Френеля

Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле - любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Слово дифракция происходит от латинского слова diffractus - преломленный.

Принцип Гюйгенса

Каждая точка волновой поверхности является источником вторичных волн, распространяющихся вперед по всем направлениям, в том числе и в область геометрической тени препятствия.

Рис. 2. Схема к принципу Гюйгенса-Френеля

Принцип Гюйгенса-Френеля

Световая волна, возбуждаемая каким-либо источником света, может быть представлена как результат суперпозиции когерентных вторичных волн, «излуча­емых» фиктивными источниками.

 

 

Метод зон Френеля

 

Волновая поверх­ность Ф  разбивается на зоны так, чтобы расстояния от краев зоны до точки наблюдения Р отличались на l/2:

 

Р₀Р-Р₁Р-Р₂Р-…= l/2,

 

тогда колебания в точку Р приходят в противофазе, и амплитуда результирую­ще­го колебания:

 

 

А = А₁ - А₂ + А₃ - А₄ + … ± А_m                                                   (1)

 

Амплитуды колебаний оценим по площадям зон Френеля. Площадь m-й зоны Френеля:

, (2)

 

где

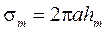    (3)

- площадь одного сегмента.

 

Из DS₀CD и DРCD:

                             (4)

 .       

 

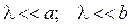
Площадь m-й зоны Френеля:

 

      (5)

 

не зависит от номера зоны m, следовательно, площади всех зон Френеля одинаковы. Вместе с тем с увеличением m возрастает угол j_m  между нормалью к поверхно­сти и направлением в точку Р, что приводит к уменьшению интен­сивности излучения m-й зоны в данном направлении, т. е. к уменьше­нию амплитуды А_m  по сравнению с амплитудами предыдущих зон. Ам­плитуда А_k  уменьшается также вследствие увеличения расстояния от зоны до точки Р с ростом j. В итоге

 

 

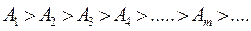
Оценка общего числа зон Френеля

.

 

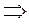
, (6)

т. е. колебания, вызываемые в точке Р полностью открытой сферической волновой поверхностью, имеют такую же амплитуду, как если бы действовала только полови­на центральной зоны Френеля. Следовательно, свет от источника S₀  в точку Р распространяется в пределах очень узкого прямого канала, т. е. прямолинейно.

Оценка радиуса луча света

; ; (7)

Дифракция Френеля на простейших преградах

1. Круглое отверстие. Пусть волна от источ­ни­ка S₀ встречает на пути не­прозрачный экран с круг­лым отверстием ВС. Диф­рак­ци­онный эффект в точке Р эк­рана зависит от числа зон Фре­неля, уклады­вающихся в отверстии:

1 зона: ;

2 зоны: ;

3 зоны: ;

m зон:   , «+»- нечетное число m, «-» четное число m;     (8)

 

39. Дифракция Фраунгофера. Дифракционная решетка,

ее разрешающая способность

Дифракция Фраунгофера на одной щели

Дифракция Фраунгофера наблюдается в том случае, когда источ­ник света и точка наблюдения бесконечно удалены от препятствия, вызывающего дифракцию, либо источник света находится в фокусе собираю­щей линзы, а дифракционная картина наблюдается в фокальной плоско­сти собирающей линзы, установленной за препятствием.

Свет дифрагирует вправо и влево от щели шириной а. Оптическая разность хода между крайними лучами FC и OE

.                    (1)

Разобьем площадь щели на зоны Френеля, ширина каждой зоны дает разность хода l/2, всего по ширине щели уместится

зон.                         (2)                   

 Вследствие дифракции световые лучи отклоняются от прямолинейного распространения на углы φ ( 0 < φ < π /2 ). Результат  дифракции в точке С_φ определится числом зон Френеля, укладывающихся в щели для данной точки.

Если число зон четное

,   ,                                (3)

в точке С_φ наблюдаетсями­нимум дифракции (они взаимно погашаются), если число зон нечетное

,                                    (4)

 

в точке С_φ наблюдается максимум дифракции.

Условие дифракционного минимума 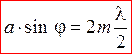,         (5)

Условие дифракционного максимума 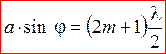 ,  (6)

Интенсивность дифракционных максимумов помере удаления от центра экрана быстро убывает. Распределение интенсивности на экране вследствие дифракции называется дифракционным спектром. Расчеты по­ка­зывают, что интенсив­ности центрального и после­дующих максимумов относятсякак

1: 0, 047: 0, 017: 0, 0083: ... ,

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: