 |
Лекция 1. Номинальная и эффективная ставки процента
|
|
|
|
При анализе и обосновании проектов с некоторым распределением доходов в течение года перед инвестором возникают различные задачи. Так оценка годовой доходности, которую обеспечивает реализация проектов, потребуется для сопоставления данного проекта с альтернативными вложениями капитала инвестора. Для этого вычисляются ставки расчетного процента, т.к. получение дохода в течение года и его капитализация позволяют увеличивать доходность такой инвестиции. Другие результаты инвестирования могут быть оценены в форме будущей стоимости будущих доходов или конечного состояния капитала инвестора, в форме потребительских доходов собственников капитала и т.д.
В ряде случаев необходимо установить следующее. Как годовая номинальная ставка банковского процента по срочным вкладам соотносится со ставкой фактически получаемого процента дохода по депозиту, который превышает эту номинальную ставку благодаря капитализации промежуточных доходов. Такая потребность может возникнуть, например, при получении доходов по банковским вкладам. Это проявляется тогда, когда начисление и капитализация процентов производится в конце каждого намеченного временного интервала. А именно, в конце месяца, квартала, полугодия и т.д.
При известном годовом проценте дохода по инвестициям вкладчики могут инвестировать ставки. Он будет начисляться по завершении каждого выделенного временного интервала на протяжении года.
Для оценки годовой доходности инвестиций в проекты, характеризуемые некоторым потоком промежуточных чистых доходов в течение года, используется понятие эффективной ставки процента (i  ). Ее иногда называют также уравновешивающей ставкой.
). Ее иногда называют также уравновешивающей ставкой.
|
|
|
Под эффективной ставкой процента (i  ) понимается годовая доходность вкладываемых в данный проект инвестиций, получаемая с учетом капитализации до конца года всех промежуточных доходов. Эффективная ставка процента может быть определена на основе следующего равенства: Будущая стоимость всех промежуточных доходов в конце года по рассматриваемому инвестиционному проекту приравнивается будущей стоимости авансированного капитала, вычисляемой с учетом эффективной ставки процента.
) понимается годовая доходность вкладываемых в данный проект инвестиций, получаемая с учетом капитализации до конца года всех промежуточных доходов. Эффективная ставка процента может быть определена на основе следующего равенства: Будущая стоимость всех промежуточных доходов в конце года по рассматриваемому инвестиционному проекту приравнивается будущей стоимости авансированного капитала, вычисляемой с учетом эффективной ставки процента.
Для простоты изложения предполагаем следующее. Пусть поток будущих доходов некоторой инвестиции, рассчитанной на один год, имеет вид Z  =(Z
=(Z 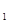 , Z
, Z  ,…,Z
,…,Z  ,…,Z
,…,Z 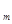 ). Т.е., будущие доходы поступают m раз в год в конце каждого выделенного подпериода. Пусть i – годовая номинальная ставка расчетного процента. Тогда начисляемый равномерно m раз в год процент i
). Т.е., будущие доходы поступают m раз в год в конце каждого выделенного подпериода. Пусть i – годовая номинальная ставка расчетного процента. Тогда начисляемый равномерно m раз в год процент i 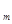 записывается в виде i
записывается в виде i 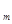 =i / m. Т.о., будущая стоимость будущих доходов, вычисляемая на основе ставки промежуточного процента, равна будущей стоимости авансированного капитала, получаемой с учетом эффективной ставки процента i
=i / m. Т.о., будущая стоимость будущих доходов, вычисляемая на основе ставки промежуточного процента, равна будущей стоимости авансированного капитала, получаемой с учетом эффективной ставки процента i  :
:
FV  =
=  Z
Z  (1+ i
(1+ i 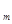 )
) 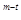 = N
= N  (1+ i
(1+ i  ) = FV
) = FV  .
.
Отсюда
i  =
=  (Z
(Z  / N
/ N  )(1+ i / m)
)(1+ i / m) 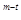 -1, (1)
-1, (1)
где N  - вкладываемые денежные средства.
- вкладываемые денежные средства.
Если проект реализуется в течение Т лет, то необходимо приравнять будущие стоимости на конец года Т. В этом случае среднегодовая эффективная ставка процента за период эксплуатации проекта выражается соотношением
i  =
=  -1. (2)
-1. (2)
Представленные формулы используются для определения годовой (1) или среднегодовой (2) доходности инвестиции при поступлении промежуточных доходов в течение года.
Для инвестиции с годовым сроком реализации и начислением промежуточных процентов на капитал предложен определенный метод расчета. Он применим, например, при вложении денежных средств N  в банк с начислением и капитализацией банковских процентов m раз в год. В основе лежит следующее равенство: Будущая стоимость будущих доходов, вычисляемых с учетом ставки промежуточного процента, равна будущей стоимости авансированного капитала, получаемой на основе эффективной ставки процента. Это равенство имеет вид:
в банк с начислением и капитализацией банковских процентов m раз в год. В основе лежит следующее равенство: Будущая стоимость будущих доходов, вычисляемых с учетом ставки промежуточного процента, равна будущей стоимости авансированного капитала, получаемой на основе эффективной ставки процента. Это равенство имеет вид:
|
|
|
N  (1+i
(1+i  ) = N
) = N  (1+i/m)
(1+i/m)  .
.
Отсюда эффективная ставка процента определяется как
i  = (1+i/m)
= (1+i/m)  -1. (3)
-1. (3)
Эта формула имеет смысл только в том случае, когда промежуточные проценты начисляют m раз в год через одинаковые интервалы времени.
Для определения ставки промежуточного процента, соответствующей заданной годовой ставке процента, при равномерном начислении промежуточных процентов, используют формулу (4):
i 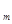 =
=  -1. (4)
-1. (4)
Если в течение года начисление процентов на вложенный капитал производится непрерывно, то для получения эффективной ставки процента можно воспользоваться следующим утверждением. При непрерывном поступлении доходов коэффициент дисконтирования будущих доходов на начало года выражается в экспоненциальной форме e  . Здесь i – номинальная ставка процента. Тогда можно показать, что коэффициент дисконтирования на конец года имеет вид e
. Здесь i – номинальная ставка процента. Тогда можно показать, что коэффициент дисконтирования на конец года имеет вид e  . Поскольку t =1, то эффективную ставку процента при непрерывном потоке доходов находят с помощью выражения
. Поскольку t =1, то эффективную ставку процента при непрерывном потоке доходов находят с помощью выражения
N  e
e  = N
= N  (1+i
(1+i  ).
).
Отсюда
i  = e
= e  - 1. (5)
- 1. (5)
Для определения годовой номинальной ставки процента, соответствующей заданной эффективной ставке при непрерывном потоке доходов, решается уравнение (5) относительно величины i. В результате получается выражение (6)
i = ln(1+i  ). (6)
). (6)
Пример
Предприниматель берет кредит на Т=5 лет в сумме К  = 100 тыс. руб. под k = 40 % годовых и обязуется вернуть долг, а также уплатить %-ты за него в конце 5-го года.
= 100 тыс. руб. под k = 40 % годовых и обязуется вернуть долг, а также уплатить %-ты за него в конце 5-го года.
Определить выплаты заемщика кредитору в конце рассматриваемого периода Т с учетом простых %-тов за кредит.
Решение
ВК  = К
= К  + k К
+ k К  Т = К
Т = К  (1+ k Т),
(1+ k Т),
ВК  = 100 + 0,4*100*5 = 300 тыс.руб.
= 100 + 0,4*100*5 = 300 тыс.руб.
Т.Е. через 5 лет необходимо вернуть 300 тыс.руб. Из них 100 тыс.руб. составит долг и 200 тыс.руб. - %-ты за кредит.
Пример
В 1994 г. “Промстройбанк” Санкт-Петербурга установил годовую номинальную ставку %-та по срочному депозиту i = 180 %.
Вклады принимались на условии ежеквартального (m = 4) начисления %-тов в течение года. Определить эффективную ставку %-та i 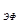 .
.
|
|
|
Решение
1) При ежемесячном начислении (m = 12) ф.(3):
i 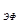 = (1+1,8/12)
= (1+1,8/12)  -1 = 4, 35 или 435 %.
-1 = 4, 35 или 435 %.
2) При ежеквартальном начислении (m = 4):
i 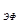 = (1+i/m)
= (1+i/m)  -1.
-1.
i 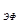 = (1+1,8/4)
= (1+1,8/4)  -1 = 3,42 или 342 %.
-1 = 3,42 или 342 %.
3) При полугодичном начислении (m = 2):
i 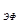 = (1+1,8/2)
= (1+1,8/2)  -1 = 2,61 или 261 %.
-1 = 2,61 или 261 %.
4) При годовом начислении (m = 1):
i 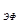 = (1+1,8/1)
= (1+1,8/1)  -1 = 1,80 или 180 %.
-1 = 1,80 или 180 %.
Чем меньше интервалы, в которые начисляются промежуточные проценты, тем выше при прочих равных условиях i  и тем выгодней клиентам банка данный вид вклада.
и тем выгодней клиентам банка данный вид вклада.
Пример
Инвестор использует при обосновании некоторой инвестиции ставку расчетного %-та i  = 80 %.
= 80 %.
Какова соответствующая этой ставке ставка промежуточного процента, если доходы поступают один раз в квартал или один раз в месяц?
Решение
1) По ф.(4) вычислим ставку промежуточного %-та, соответствующую эффективной ставке i  = 80 %. При ежеквартальном поступлении доходов (m = 4)
= 80 %. При ежеквартальном поступлении доходов (m = 4)
i  =
=  -1
-1
i  =
= 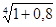 - 1 = 0,158 или 15.8 %.
- 1 = 0,158 или 15.8 %.
2) При ежемесячном поступлении доходов (m = 12) ставка промежуточного процента
i  =
= 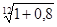 - 1 = 0,05 или 5 %.
- 1 = 0,05 или 5 %.
Пример
Инвестор может поместить деньги в банк под i  = 80 % годовых на Т= 1 год или финансировать проект с непрерывным потоком доходов в течение того же периода при годовой номинальной ставке расчетного процента i = 60 %. Определить, какой проект предпочтительнее по годовой доходности.
= 80 % годовых на Т= 1 год или финансировать проект с непрерывным потоком доходов в течение того же периода при годовой номинальной ставке расчетного процента i = 60 %. Определить, какой проект предпочтительнее по годовой доходности.
Решение
1) Выделим эффективную ставку %-та для инвестиции с непрерывным потоком доходов (ф.5)
i  = e
= e  - 1 = e
- 1 = e  - 1 = 0,822 или 82.2 %,
- 1 = 0,822 или 82.2 %,
что больше доходности банковского вклада.
2) Можно вычислить предельную годовую номинальную доходность инвестиции с непрерывным потоком доходов, при которой вложения в банк с учетом данной ставки банковского %-та оказываются более выгодными. Для этого определим номинальную ставку %-та, соответствующую эффективной, равной i  = 80 %, при непрерывном потоке доходов (ф.6).
= 80 %, при непрерывном потоке доходов (ф.6).
i = ln(1+i  ) = ln(1+0,8) = 0.588 или 58.8 %.
) = ln(1+0,8) = 0.588 или 58.8 %.
Т.о., до тех пор, пока номинальная доходность инвестиционного проекта с непрерывным потоком инвестиций составляет не более 58,8 %, выгоднее вкладывать в банк. В противном случае, инвестиции – в проект.
|
|
|


