Лекция 5. Дисконтирование и учет по простым ставкам

 

При экономической оценке инвестиций часто возникают задачи, которые являются обратными определению наращенной суммы. Так, по заданной сумме S, которую необходимо будет уплатить через некоторое время n, следует определить сумму полученной ссуды P. Такие расчеты могут потребоваться, например, при разработке условий инвестиционных контрактов. Кроме того, необходимость в расчете P по S возникает и тогда, когда необходимо удержать проценты с суммы S непосредственно при выдаче ссуды. При этом сумма S дисконтируется, а процесс начисления и удержания процентов вперед называется учетом. Проценты в виде суммы S – P = D называются дисконтом. Потребность в дисконтировании возникает, например, при покупке банком или другим финансовым учреждением краткосрочных обязательств (векселей, тратт и т.д.), оплата которых должником производится в будущем.

Тратта (итал. tratta) – это переводной вексель. Представляет собой письменный приказ кредитора заемщику (или обычно банку) об уплате последним определенной суммы денег третьему лицу (ремитенту) или предъявителю тратты. Используется чаще всего в расчетах по внешней торговле.

Понятие дисконтирования употребляется и в более широком смысле. Это метод определения любой стоимостной величины на некоторый момент времени при условии, что в будущем она составит величину S, вне зависимости от того, имела ли место финансовая операция, предусматривающая начисление процентов, или нет. В качестве финансовой операции может быть кредитование, выдача денег в долг и т.д. Этот расчет также называют приведением стоимостного показателя к заданному моменту времени. Найденную величину P путем дисконтирования суммы S называют современной, или приведенной, величиной S (present value). Данное понятие является одним из важнейших в современном количественном анализе финансовых операций, т.к. с помощью дисконтирования учитывается такой фактор, как время.

В зависимости от вида процентной ставки применяют два вида дисконтирования – математическое дисконтирование и банковский (коммерческий) учет.

Математическое дисконтирование. Математическое дисконтирование является решением задачи, обратной наращению первоначальной суммы ссуды, депозита и т.д. В этом случае условие задачи формулируется следующим образом: Какую первоначальную сумму Р надо выдать в долг, чтобы при начислении на нее процентов по ставке i к концу оговоренного срока получить наращенную сумму, равную S. Величина Р рассчитывается с помощью формулы

 

Р = S , (1)

 

где

n = д / К – продолжительность ссуды в годах;

 - дисконтный множитель;

д - срок наступления платежа, дней;

К = 365, количество дней в году.

Дисконтный множитель показывает, какую долю составляет Р в сумме S. Разность S – P в этом случае рассматривают не только как абсолютную величину процентов, начисленных на Р, но и как дисконт суммы S, обозначаемый как D .

Банковский учет (учет векселей). Суть операции учета заключается в следующем. Банк или какое-либо другое финансовое учреждение до наступления срока платежа по векселю или другому платежному обязательству покупает его у владельца по цене, меньше той суммы, которая должна быть выплачена по нему в конце срока. Это значит, что банк приобретает (или учитывает) его с дисконтом. Получив при наступлении срока векселя деньги, банк таким образом реализует дисконт в свою пользу. Владелец векселя, с помощью его учета, имеет возможность получить деньги раньше указанного на нем срока. При учете векселей применяется банковский, или коммерческий, учет (bank discount). Согласно этому методу проценты за пользование ссудой начисляются на сумму, подлежащую уплате в конце срока ссуды (maturity value). При этом применяется учетная ставка d, измеряемая в десятичных дробях. По определению простая годовая учетная ставка находится как d = (S –P) /S. При этом простая ставка процентов равна отношению i = (S –P) /P. Величина дисконта или учета D , удерживаемого банком, равен Snd. Отсюда

 

P = S – Snd = S(1 – nd), (2)

 

где n – продолжительность срока в годах от момента учета до даты уплаты по векселю;

(1 – nd) – дисконтный множитель.

Чаще всего дисконтирование по учетной ставке производится при условии, что год равен 360 дням (К=360), а число дней в периоде берется точным. Смысл учета по простой учетной ставке рассмотрим с помощью графика на рис.1. Здесь показан процесс дисконтирования суммы S, которая должна быть уплачена спустя время n после начального момента. Если учет производится на этот момент, то сумма после вычета дисконта составит величину Р. Если же учет производится за время n  до наступления срока платежа, то искомая сумма равна P = S - Sn d. Учет портфеля векселей называется операцией “ а форфе ” (a forfeit) – целиком, общей суммой с последовательными сроками уплаты по ним.

Область применения учетных ставок не ограничивается учетом векселей. Этот вид ставок может использоваться и в других видах финансово-кредитных операций. При этом термин “учетная ставка” иногда не вполне корректно применяется в более широком смысле – как синоним процентной ставке вообще.

 

Рис. 1. Процесс дисконтирования суммы

O

P

S

 

 

Но надо обратить внимание на то, что рассмотренные два метода дисконтирования – по ставкам i и d – приводят к разным финансовым результатам. Заметим, что учетная ставка отражает фактор времени более “жестко”. Так, из формулы (2) следует, что при n 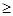 1/ d величина Р станет отрицательной. Иначе говоря, при относительно большом сроке уплаты по векселю и высокой учетной ставке дисконт может привести к нулевой или даже отрицательной сумме Р. А это, разумеется, лишено смысла. Например, при d = 0,2 уже пятилетний срок достаточен для того, чтобы сторона, учитывающая вексель, ничего не получила по нему. Такая ситуация не может при математическом дисконтировании: при любом сроке современная величина платежа здесь получается больше нуля. Для иллюстрации в таблице 1 приведем дисконтные множители, рассчитанные для одного и того же значения простой ставки процентов и учетной ставки.

Таблица 1 - Дисконтные множители (i = d = 10%)

Вид ставки	N
	1/12	1/4	1/2	1	2	10
i	0,99174	0,97561	0,95238	0,90909	0,83333	0,5
d	0,99167	0,975	0,95	0,9	0,8	0

 

Наращение по учетной ставке. Простая учетная ставка может быть применена и при расчете наращенной суммы. В этом возникает необходимость, в частности. При определении суммы, которую надо проставить в бланке векселя, если заданы текущая сумма долга, его срок и учетная ставка. Наращенная сумма

 

S = P , (3)

 

где  - множитель наращения;

n – продолжительность ссуды в годах.

При n =1 / d расчет по формуле (3) лишен смысла, так как наращенная сумма становится бесконечно большим числом. Простая учетная ставка дает более быстрый рост ссуды, чем аналогичная по величине ставка простых процентов. Проиллюстрируем это в таблице 2.

 

Таблица 2 - Множители наращения по простой ставке процентов и учетной ставке (i = d = 10%)

Вид ставки	N
	1/12	1/4	1/2	1	2	10
i	1,0083	1,025	1,05	1,1	1,2	2
d	1,0084	1,0256	1,0526	1,1111	1,25

Пример

Через д=180 дней с момента подписания контракта должник уплатит S=31 тыс. у.д.е. Кредит предоставлен под i = 6% годовых. Определить, какую сумму получит должник и сумму дисконта.

Решение

При условии, что временная база равна К= 365 дням, по ф.(1) находим

Р = S 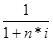= 31000  = 30109,1 у.д.е.;

D = S – P = 890,9 у.д.е.

Пример

Тратта (переводной вексель) выдана на сумму S=100 тыс. у.д.е. с уплатой 17.11. Владелец документа учел его в банке 23.09 по учетной ставке d = 8%.

Решение

Так как оставшийся до погашения обязательства период равен д=55 дням, то при К=360 дням полученная сумма (без уплаты комиссионных) по ф.(2) составит

P = S – Snd = S(1 – nd) = 100000(1 -  0,08) = 98777,78 у.д.е.

Величина дисконта определится

D = S – P = 100000 – 98777,78 = 1222,22 у.д.е.

Пример

Ссуда в размере Р = 100 тыс. у.д.е. выдана 20.01 до 05.10 включительно под d = 8 % годовых, год невисокосный. Найти наращенную сумму при условии, что проценты начисляются по простой учетной ставке.

Решение

1) Точное число дней ссуды составит (дата 05.10 соответствует 278 дням):

д = 278 – 20 = 258 дней.

2) Тогда наращенная сумма по ф.(3) определятся как:

S = P  = 100000  = 106082,04 у.д.е.

Пример

Ссуда в размере Р = 100 тыс. у.д.е. выдана 20.01 до 05.10 включительно под d = 8 % годовых, год невисокосный. Необходимо найти размер погасительного платежа.

Решение

1) Точное число дней ссуды составит (дате 05.10 соответствует 278 дней):

д = 278 – 20 = 258 дней.

Тогда точные проценты с точным числом дней ссуды определятся как:

S = P(1+д/К*0,08) = 100000(1+ 0,08) = 105654,79 у.д.е.

2) Обыкновенные проценты с точным числом дней ссуды учитываются как:

S = P(1+д/К*0,08) = 100000(1+ 0,08) = 105733,33 у.д.е.

3) Приближенное число дней ссуды составит:

д = 8*30+11+5 – 1 = 255 дней.

Обыкновенные проценты с приближенным числом дней ссуды определятся как:

S = P(1+д/К*0,08) = 100000(1+ 0,08) = 105666,67 у.д.е.

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: