 |
Методы решения систем линейных алгебраических уравнений
|
|
|
|
Лабораторная работа №7
Методы решения системы линейных алгебраических уравнений
Цели работы:
· знакомство с функциями для работы с массивами;
· разработка алгоритмического и программного обеспечения решения системы линейных алгебраических уравнений.
Необходимое оборудование и материалы.
· ОС Windows XP, Vista, 7;
· Matlab 6.5 или 7.x;
· ПК класса не ниже Pentium II, RAM 128Mb.
Трудоемкость: 4 академических часа.
Системы линейных алгебраических уравнений
Рассмотрим систему линейных алгебраических уравнений (СЛАУ) относительно n неизвестных x1, x2,..., xn:
Эта система в "свернутом" виде может быть записана так:
, i=1,2,..., n.
В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричной форме Ax=b, где
, 
, 
.
Матрица A, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками – коэффициенты при неизвестных в соответствующем уравнении называется матрицей системы. Матрица-столбец b, элементами которой являются правые части уравнений системы, называется матрицей правой части или просто правой частью системы. Матрица-столбец x, элементы которой – искомые неизвестные, называется решением системы.
Система линейных алгебраических уравнений, записанная в виде Ax=b, является матричным уравнением.
Матрица, получаемая при сцеплении матрицы системы и правой части, называется расширенной матрицей. Размер расширенной матрицы равен 
.
СЛАУ называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
СЛАУ совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.
|
|
|
Рангом системы строк (столбцов) матрицы А называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов и это число называется рангом матрицы.
Вырожденной или сингулярной называют квадратную матрицу, определитель которой равен нулю.
Невырожденная матрица – квадратная матрица, определитель которой отличен от нуля. В противном случае она называется вырожденной.
Для квадратной матрицы М невырожденность эквивалентна каждому из следующих условий:
· M обратима, то есть существует обратная матрица;
· строки (столбцы) матрицы M линейно независимы;
· элементарными преобразованиями строк (столбцов) матрицу M можно привести к единичной матрице;
· ранг матрицы равен её размерности.
Функция r = rank(A) возвращает ранг матрицы (если ранг системы полный, то система невырождена)
Функция d = det(A) вычисляет определитель квадратной матрицы; если матрица A целочисленная, то результатом является также целое число.
Обратной к квадратной невырожденной матрице 
называется такая матрица 
, которая при умножении на справа и слева дает в результате единичную матрицу. Встроенная функция inv обращает матрицу, ее входным аргументом является исходная матрица, а выходным – обратная.
Табл. 1.Варианты задания.
| № варианта | Система линейных уравнений | № варианта | Система линейных уравнений |
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
|
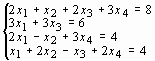
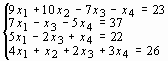
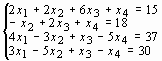
Задание 1.
1. Приведите систему линейных алгебраических уравнений к матричной форме. Системы уравнений и варианты заданий представлены в табл. 1. Номер варианта совпадает с номером студента в карточке подгруппы.
|
|
|
2. Убедитесь, что матрица системы является невырожденной. Если матрица системы является вырожденной, обратитесь к преподавателю.
3. Если матрица системы невырожденная, найдите обратную матрицу. Проверьте результат умножением справа и слева полученной матрицы на исходную.
Методы решения систем линейных алгебраических уравнений
|
|
|
