 |
Решение матричного уравнения с помощью обратной матрицы
|
|
|
|
Если матрица системы невырождена, то у нее существует обратная матрица и тогда решение системы 
дается формулой:
.
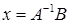Вычисление решения системы линейных уравнений по формулам Крамера
Справедливо следующее утверждение (формулы Крамера).
Если определитель D=det A матрицы системы Ax=b отличен от нуля, то система имеет единственное решение x1, x2,..., xn, определяемое формулами Крамера
xi = D i / D, i=1,2,..., n,
где D i – определитель матрицы n -го порядка, полученной из матрицы A системы заменой i -го столбца столбцом правых частей b.
Пример 1.
Программа, которая находит первое неизвестное в системе линейных алгебраических уравнений
.
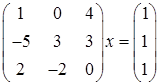% задаем СЛАУ
A=[1 0 4;
-5 3 3;
2 -2 0];
B=[1;1;1];
% копируем значение матрицы A
A1=A
% подставляем в первый столбец правую часть
A1(:,1)=B
% находим первое неизвестное
x1=det(A1)/det(A)
Решение системы линейных уравнений методом Гаусса
Метод Гаусса основан на приведении методом исключения СЛАУ к треугольному виду (прямой ход):
,
а затем проводится решение этой системы начиная с xn и т.д. (обратный ход).
Под главным в методе Гаусса понимается максимальный по модулю элемент в 
-ом столбце среди всех строк, начиная с -ой. Иными словами, в строках 
главный элемент находиться не может
Алгоритм решения системы из n уравнений методом Гаусса с выбором главного элемента по столбцам выглядит следующим образом.
Прямой ход.
Формируется матрица расширенной системы 
Выполняется цикл от 1 до 
по :
На шаге выбирается главный элемент в -ом столбце. Пусть это будет элемент в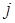 
-ой строке 
.
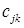Перестановко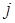й и строк делает этот элемент диагональным.
Далее производим исключение 
из уравнений с номерами 
с помощью соотношения:
|
|
|
Выполняется цикл от 
до по :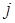
Если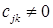 
, то 
, где
,
, 
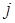– -ая и -ая строки матрицы 
соответственно.
Конец цикла по .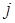
Конец цикла по .
После 
шагов приходим к системе уравнений с треугольной матрицей.
Пример решения СЛАУ методом Гаусса рассмотрен в приложении.
Все действия в методе Гаусса относятся к элементарным операциям над строками, что не приводит к изменению решения.
Под элементарными операциями понимаются следующие операции:
· перестановка строк;
· умножение строки на число, отличное от нуля;
· сложение строки матрицы с другой строкой, умноженной на отличное от нуля число).
Обратный ход.
Перед началом второго этапа, называемого обратным ходом, имеется верхняя треугольная матрица расширенной системы.
Выделяем из расширенной матрицы системы матрицу системы и правую часть.
Из последнего уравнения системы находим
.
Далее находим оставшиеся неизвестные из соотношения
.
Задание 2.
1. Составьте структурные схемы алгоритмов решения системы линейных алгебраических уравнений методом Крамера, Гаусса и с помощью обратной матрицы. Структурные схемы должны включать ввод матрицы системы и правой части, проверку невырожденности матрицы системы, процесс получения решения и вывод результата. Размер СЛАУ должен быть произвольным.
2. Напишите функции, реализующие структурные схемы решения СЛАУ тремя методами.
3. Решите СЛАУ из табл. 1 с помощью полученных в предыдущем пункте функций. Результаты занесите в сводную таблицу.
Приложение. Пример решения СЛАУ методом Гаусса
Рассмотрим СЛАУ
.
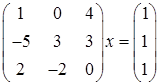Прямой ход.
Формируем матрицу расширенной системы.
C=[A B]
C =
1 0 4 1
-5 3 -3 1
2 -2 0 1
Находим главный элемент в первом столбце
first=C(1:3,1) % первый столбец (строки с текущей по третью)
[fake,m]=max(abs(first)); % m – индекс главного элемента
ind = m;
Делаем главный элемент диагональным с помощью перестановки строк
|
|
|
r=C(1,:);
C(1,:)=C(ind,:);
C(ind,:)=r
C =
-5 3 -3 1
1 0 4 1
2 -2 0 1
Путем элементарных преобразований над строками (умножение строки на число 
и сложение строк), получаем нулевые элементы под главной диагональю.
if C(2,1)~=0
mu_21=C(1,1)/C(2,1);
C(2,:)=C(1,:)-mu_21*C(2,:);
end
if C(3,1)~=0
mu_31=C(1,1)/C(3,1);
C(3,:)=C(1,:)-mu_31*C(3,:);
end
C =
-5.0000 3.0000 -3.0000 1.0000
0 3.0000 17.0000 6.0000
0 -2.0000 -3.0000 3.5000
Далее переходим ко второму столбцу.
Находим главный элемент второго столбца путем сравнения элементов из второй и третьей строки и выбора максимального по модулю элемента
second=C(2:3,2) % элементы текущего столбца со второго по третий
[fake,m]=max(abs(second)); % индекс максимального элемента из двух
ind=m+1; % индекс главного элемента во втором столбце матрицы системы
Делаем главный элемент диагональным.
r=C(2,:);
C(2,:)=C(ind,:);
C(ind,:)=r
C =
-5.0000 3.0000 -3.0000 1.0000
0 3.0000 17.0000 6.0000
0 -2.0000 -3.0000 3.5000
Путем элементарных преобразований над строками (умножение строки на число и сложение строк), получаем нулевые элементы под главной диагональю.
if C(3,2)~=0
mu_32=C(2,2)/C(3,2);
C(3,:)=C(2,:)-mu_32*C(3,:);
end
C =
-5.0000 3.0000 -3.0000 1.0000
0 3.0000 17.0000 6.0000
0 0 12.5000 11.2500
Получена верхняя треугольная матрицы. Все элементы главной диагонали отличны от нуля, поэтому матрица системы невырождена.
Прямой ход метода Гаусса закончен.
|
|
|
