 |
Дизъюнктивные нормальные формы
|
|
|
|
ЗАДАЧИ МИНИМИЗАЦИИ БУЛЕВЫХ ФУНКЦИЙ
Выражение вида
называется дизъюнктивной нормальной формой (ДНФ). Здесь 
есть элементарная конъюнкция (состоит из попарно различных литералов), 
– ранг i -ой конъюнкции (число литералов в элементарной конъюнкции), m – длина ДНФ (число слагаемых). Если ранг 
, то элементарная конъюнкция называется пустой. При m =0 ДНФ полагается равной нулю и называется пустой. 
Минимальной ДНФ функции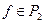 
называется ДНФ, содержащая наименьшее число литералов по сравнению со всеми другими ДНФ, реализующими данную функцию.
Пример 5.1. Рассмотрим функцию 
. Ее можно представить в виде двух различных ДНФ 
и 
. При этом 
содержит только два литерала, а 
содержит шесть литералов.
Кратчайшей ДНФ функции 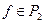называется ДНФ, содержащая наименьшее число элементарных конъюнкций по сравнению со всеми другими ДНФ, реализующими данную функцию.
Пример 5.2. Для функции можно записать ДНФ 
, 
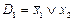и 
. При этом и 
имеют по две элементарные конъюнкции, а 
имеет три элементарные конъюнкции. ДНФ и являются кратчайшими, при этом является минимальной.
Сложностью минимальной ДНФ 
булевой функции называется число входящих в нее литералов. Сложностью кратчайшей ДНФ булевой функции называется число входящих в нее элементарных конъюнкций.
Задача минимизации ДНФ заключается в построении для произвольной 
ее минимальной или кратчайшей ДНФ. Минимальная (кратчайшая) ДНФ булевой функции может оказаться не единственной.
Утверждение. Число различных ДНФ, составленных из переменных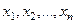 
, равно 
.
Доказательство. Т.к. любая переменная может входить в произвольную конъюнкцию без инверсии, с инверсией или не входить вообще, то число различных элементарных конъюнкций, построенных из 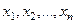есть 
. Каждая конъюнкция либо входит, либо не входит в ДНФ, следовательно, число различных ДНФ есть 
¡.
|
|
|
Множество 
называется единичным покрытием функции . Для любой функции существует единичное покрытие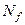 
и это соответствие является взаимнооднозначным. Говорят, что функция 
поглощает функцию 
, если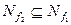 
.
Пример 5.3. Для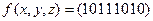 
построим единичное покрытие. Запишем таблицу истинности функции.
| x | y | z | 
|
Отметим на кубе 
единичные наборы черными точками:
Рис. 5.1.
.
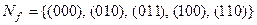Подмножество 
есть интервал ранга r, соответствующий элементарной конъюнкции 
. Число 
называется размерностью интервала 
. Интервал можно рассматривать как множество наборов (вершин из 
), у которых 
координат зафиксировано 
..., 
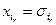, а остальные 
– принимают произвольные значения из множества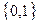 
. На рис. 5.2. приведены различные интервалы.
Рис. 5.2.
Для любой ДНФ 
функции , где 
элементарная конъюнкция, выполняется теоретико-множественное соотношение
и обратно. Если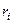 
– ранг интервала 
, то сумма 
совпадает с числом литералов в ДНФ . В теоретико-множественной постановке задача построения минимальной ДНФ сводится к отысканию такого покрытия 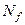интервалами 
, чтобы сумма рангов была минимальной. При поиске кратчайшей ДНФ следует минимизировать число интервалов, входящих в покрытие.
Как известно, булева функция определяется заданием ее значений на 
наборах. Построим такую таблицу, которая позволит установить взаимно однозначное соответствие между каждой клеткой таблицы и некоторой вершиной (двоичным набором) куба . Кодирование клеток таблицы будем осуществлять так, чтобы соседние (по строке или столбцу) клетки отличались значением только одной переменной в соответствующих им двоичных кодах вершины куба 
. Кодирование таблиц, позволяющее получить указанное выше свойство соответствия клеток таблицы вершинам куба Bn, обеспечивается за счет применения циклического симметричного кода Грея.
|
|
|
Пусть 
– двоичный набор, являющийся представлением целого числа
,
тогда код Грея 
, соответствующий двоичному набору определяется по следующему правилу
Кодирование таблиц осуществляется следующим образом. Переменные 
разбиваются на две группы 
и 
, где 
– наименьшее целое, большее или равное 
. Первая группа переменных используется для кодирования по строкам таблицы, вторая – по столбцам. Если при перечислении двоичных наборов, приписанных клеткам таблицы, используется код Грея, то такая таблица называется картой Карно.
Рассмотрим карты Карно для случаев 
. На рис. 5.3 показано как происходит кодирование наборов.
Рис. 5.3.
Карты Карно при n =1,2 приведены на рис. 5.4 (а, б), при n =3 – на рис. 5.5, при n =4 – на рис. 5.6.
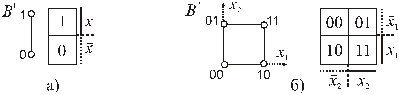
Рис. 5.4.
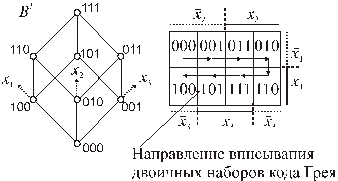
Рис. 5.5. Рис. 5.6.
Пример 5.4. Рассмотрим задание функций при помощи карт Карно.
а) Для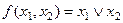 
карта Карно имеет вид
Рис. 5.7.
б) Пусть функция задана при помощи карты Карно:
Рис. 5.8.
Выделим интервалы на карте
Рис. 5.9.
.
и запишем функцию в виде ДНФ: 
. На рис. 5.9 видно, что 
, т.е. покрытие функции 
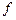образуют три интервала. Если из этого покрытия удалить интервал 
, то оставшиеся два интервала покроют все точки множества :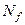
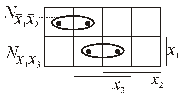
Рис. 5.10.
и для данной функции ее минимальная и кратчайшая ДНФ будет иметь вид 
.
|
|
|
