 |
Способы построения сокращенной ДНФ
|
|
|
|
Импликантом функции  называется элементарная конъюнкция K такая, что
называется элементарная конъюнкция K такая, что  . Импликант называется простым, если после удаления любого его сомножителя он перестает быть импликантом функции
. Импликант называется простым, если после удаления любого его сомножителя он перестает быть импликантом функции  .
.
Интервал  функции
функции  называется максимальным, если
называется максимальным, если  и не существует другого интервала
и не существует другого интервала  такого, что
такого, что  . Т.е. интервал
. Т.е. интервал  является максимальным тогда и только тогда, когда K – простой импликант функции
является максимальным тогда и только тогда, когда K – простой импликант функции 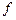 . Отсюда
. Отсюда

–  единичное покрытие есть объединение всех максимальных интервалов.
единичное покрытие есть объединение всех максимальных интервалов. 
ДНФ  , реализующая функцию
, реализующая функцию 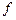 и соответствующая покрытию множества
и соответствующая покрытию множества  всеми максимальными интервалами, называется сокращенной ДНФ функции
всеми максимальными интервалами, называется сокращенной ДНФ функции 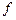 . Сокращенная
. Сокращенная  ДНФ для данной функции
ДНФ для данной функции 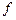 определяется однозначно.
определяется однозначно.
Теорама 5.1. Любая минимальная ДНФ функции  , не совпадающая с ее сокращенной ДНФ, может быть получена из сокращенной путем удаления некоторых простых импликант.
, не совпадающая с ее сокращенной ДНФ, может быть получена из сокращенной путем удаления некоторых простых импликант.
Теорема 5.2. Сокращенная ДНФ любой монотонной функции алгебры логики не содержит отрицания переменных и является ее единственной минимальной и кратчайшей ДНФ.
ДНФ  , реализующая функцию f и состоящая только из простых импликант,
, реализующая функцию f и состоящая только из простых импликант,  называется тупиковой для f, если удаление из нее хотя бы одной конъюнкции приводит к ДНФ,
называется тупиковой для f, если удаление из нее хотя бы одной конъюнкции приводит к ДНФ,  не реализующей функцию f.
не реализующей функцию f.
Покрытие множества 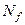 максимальными интервалами называется неприводимым,
максимальными интервалами называется неприводимым,  если после удаления из него любого интервала оно перестает быть покрытием.
если после удаления из него любого интервала оно перестает быть покрытием. 
Рассмотрим методы построения сокращенной ДНФ. Используем правила
| склеивания | 
| (5.1) |
| поглощения | 
| (5.2) |
| неполного склеивания | 
| (5.3) |
| обобщенного склеивания | 
| (.4) |
Здесь  некоторые элементарные конъюнкции.5
некоторые элементарные конъюнкции.5
Метод Блейка построения сокращенной ДНФ  булевой функции состоит в последовательном применении правил (5.2) и (5.4).
булевой функции состоит в последовательном применении правил (5.2) и (5.4).  Сначала применяется правило (5.4) пока это возможно, а затем – (5.2).
Сначала применяется правило (5.4) пока это возможно, а затем – (5.2).
|
|
|
Пример 5.5. Используя метод Блейка, построить сокращенную ДНФ функции  .
.
Решение.  =
=
(одинарной линией подчеркнуты слагаемые, которые при помощи правила (5.4) дают новую элементарную конъюнкция, которая выделена двойным подчеркиванием)



 .
.
Далее применяется правило поглощения (подчеркнуты слагаемые, поглощаемые по правилу (5.2) переменной  ):
):

 =
=  .
.
Слагаемое  поглощается по правилу (5.2) слагаемым
поглощается по правилу (5.2) слагаемым  . Таким образом, получили сокращенную ДНФ
. Таким образом, получили сокращенную ДНФ  .
.
Рассмотрим  табличный метод построения минимальной ДНФ, основанный на использовании карт Карно.
табличный метод построения минимальной ДНФ, основанный на использовании карт Карно.
Пример 5.6. Используя карту Карно, построить все минимальные ДНФ функции  .
. 
Решение. Строим покрытие всеми максимальными интервалами и выпишем соответствующую этому покрытию сокращенную ДНФ.

Рис. 5.11.
Сокращенная ДНФ данной функции имеет вид
 .
.
Построим неприводимое покрытие и выпишем все тупиковые ДНФ, реализующие заданную функцию  .
.

Рис. 5.12.
 ,
,
где L – число литералов в ДНФ.

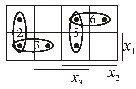
Рис. 5.13. Рис. 5.14.
 .
.  .
.


Рис. 5.15. Рис. 5.16.
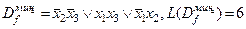 .
.  .
.
Из полученных тупиковых ДНФ выберем те, которые имеют наименьшее число литералов и выпишем минимальные ДНФ:
 ;
; 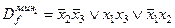 .
.
Рассмотрим геометрический метод нахождения сокращенной (минимальной, кратчайшей) ДНФ, который нагляден для небольшой размерности  .
.
Пример 5.7. Используя геометрический метод, построить все минимальные ДНФ функции 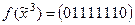 .
.
Решение. Строим покрытие куба  максимальными интервалами (рис. 5.17) и выпишем соответствующую этому покрытию сокращенную ДНФ: максимальными интервалами (рис. 5.17) и выпишем соответствующую этому покрытию сокращенную ДНФ:
 .
Построим теперь неприводимое покрытие и выпишем все тупиковые ДНФ, реализующие заданную функцию .
Построим теперь неприводимое покрытие и выпишем все тупиковые ДНФ, реализующие заданную функцию  . .
|  Рис. 5.17.
Рис. 5.17.
| |
 Рис. 5.18.
Рис. 5.18.
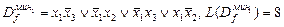 . .
|  Рис. 5.19.
Рис. 5.19.
 . .
| |
 Рис. 5.20.
.
Рис. 5.20.
.  . .
|  Рис. 5.21.
Рис. 5.21.
 . .
| |

Рис. 5.22.

Выпишем теперь все минимальные ДНФ, реализующие функцию  (содержат наименьшее число литеров среди всех ДНФ, реализующих данную функцию).
(содержат наименьшее число литеров среди всех ДНФ, реализующих данную функцию).
|
|
|
 ,
,  .
.
Рассмотрим метод построения сокращенной ДНФ из конъюнктивной нормальной формы. В качестве исходного задания функции берется ее КНФ, затем производится перемножение скобок, согласно дистрибутивному закону, а после – при помощи правила поглощения, удаляются лишние слагаемые. В результате получается сокращенная ДНФ.
Пример 5.8. Построить сокращенную ДНФ по заданной КНФ функции  .
.
Решение. Раскрываем скобки  =
=




 .
.
Теорема 5.3 (теорема Квайна). Если, исходя из совершенной ДНФ функции, произвести все возможные операции неполного склеивания, а затем – элементарного поглощения, то в результате получится сокращенная ДНФ, т. е. дизъюнкция всех простых импликант.
Рассмотрим алгоритм Квайна построения сокращенной ДНФ. Сперва к совершенной ДНФ функции применяется правило неполного склеивания (5.3) (к каждой паре конъюнкций), а затем при помощи операции поглощения (5.2) удаляются те конъюнкции ранга n, которые могут быть удалены. В результате получается некоторая ДНФ  . Процедура повторяется, и на (k +1)-м шаге операции неполного склеивания и поглощения применяются к конъюнкциям ранга
. Процедура повторяется, и на (k +1)-м шаге операции неполного склеивания и поглощения применяются к конъюнкциям ранга  ДНФ
ДНФ  . В результате получается ДНФ
. В результате получается ДНФ 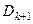 . Алгоритм завершается, если
. Алгоритм завершается, если  =
= 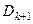 .
.
Пример 5.9. Пусть функция f задана своей совершенной ДНФ.
 .
.
Применим к ней алгоритм Квайна получения сокращенной ДНФ. Для этого для первой конъюнкции попарно применяем правило (5.3), затем для второй и т.д. (первая с третьей, вторая с третьей, вторая с четвертой, третья с пятой), после чего применяется правило (5.2). На первом этапе получим  . На втором этапе правило (5.3) в
. На втором этапе правило (5.3) в  применяется ко второй и пятой, третьей и четвертой конъюнкциям, а затем правило (5.2). Поэтому получим
применяется ко второй и пятой, третьей и четвертой конъюнкциям, а затем правило (5.2). Поэтому получим  .
.
|
|
|


