Измерение сопротивлений мостом Уитстона

Мостовые схемы

Как отмечалось выше, мостовые схемы позволяют исключить постоянную составляющую измеряемого напряжения. Мостовая схема представляет собой двойной потенциометр с дифферен­циальным включением.

Рассмотрим вопросы линеаризации характеристик мостовых схем и компенсации влияющих величин.

Преимущества мостовых схем — в большей, чем присущей потенциометрическим измерительным схемам, точности и мень­шей чувствительности к шумам и дрейфу параметров источника питания. Эти основные достоинства мостов можно показать на примере резистивного моста (рис. 3.12).

 

С учетом флуктуации Д* э.д.с е_з0 источника напряжения в точках А и В диагонали моста равны

В положении равновесия моста

Выходное напряжение v_m, представляющее собой разность напряжений va—vb, определяется выражением

 

Сравнение с потенциометрической схемой (разд. 3.23) показы­вает, что влияние флуктуации на выходное напряжение в мостовой схеме существенно уменьшается, если .

Измерение сопротивлений мостом Уитстона

Условия равновесия и разбаланса. Общая схема моста Уит­стона показана на рис. 3.13. Эд.с. , Rs — внутреннее сопротивление источника, R_d — входное сопротивление устройст­ва, измеряющего ток или напряжение разбаланса в диагонали моста. По уравнениям Кирхгофа можно определить ток i_d в диагонали моста

Мост находится в равновесии, когда v_a=v_b, при этом i_d=0, что обусловлено соотношением R₁R₄₌R₂R₃

Условие равновесия зависит только от сопротивления плеч мос­та, оно не зависит от внутреннего сопротивления источника пи­тания и входного сопротивления прибора, измеряющего ток или напряжение в диагонали.

Обычно мост питают источником, внутреннее сопротивление которого мало: идеальном случае Rs=0 выражение для U упрощается:

Когда измерительное устройство (осциллограф, вольтметр или усилитель) имеет большое входное сопротивление R_d>> R₁,R₂,R₃,R₄, имеем

В последующем изложении материала будем исходить из этих соотношений.

Мост Унтстона представляет собой двойной потенциометр; его чувствительность максимальна в положении равновесия, когда R₁= R₂ и R₃= R₄.

Для упрощения измерений часто выбирают сопротивления плеч моста одинаковыми: R₁=R₂=R₃=R₄=R₀. При одновременном изменении сопротивлений всех плеч моста

напряжение разбаланса будет определяться соотношением

В этом случае напряжение разбаланса является нелинейной функцией вызвавших его изменений сопротивлений плеч моста. Если переменным является только одно сопротивление, напри­мер, R_2,то

На рис. 3.14,а представлена диаграмма отношения v_m/e_s в функции относительного изменения R/R₀ одного из сопро­тивлений моста, первоначально находившегося в положении равновесия. Эта зависимость линейна в относительно узком диапазоне изменения R₀ в обе стороны от положения равнове­сия (рис. 3.14,6). Когда сопротивление R_S того же порядка, что и сопротивления плеч моста, a R_d намного больше, напряжение разбаланса можно выразить формулой

При прочих равных условиях возрастание сопротивления источника приводит к уменьшению чувствительности мостовой схемы. В этом случае, если переменным является только одно сопротивление, например R₂, напряжение разбаланса выражается соотношением

В случае, когда мост питается источником тока, внутреннее со­противление такого источника намного больше сопротивлений плеч моста. С учетом тока источника i_s=e_s/R_S напряжение разбаланса можно записать в виде

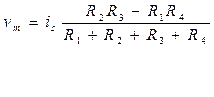
Если сопротивления всех плеч моста с источником тока одно­временно изменяются относительно значения R₀, соответствую­щего положению равновесия, то напряжение разбаланса v_m в функции этих изменений

Если в мосте с источником тока изменяется только одно из со­противлений, например, R₂ ,имеем

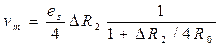
Сравнение последнего выражения с выражением для напряже­ния разбаланса моста, питаемого источником напряжения, пока­зывает преимущество питания источником тока, так как пря этом уменьшается нелинейность характеристики преобразова­ния схемы.

Линеаризация характеристики преобразования и компенса­ция воздействия влияющих величин. Работа на малом участке характеристики. Мост из четырех одинаковых сопротивлений R₀, вариации которых малы, , с точностью до величин второго порядка линеен близ положения равновесия;

Это соотношение отражает очень важное свойство моста, у ко­торого все плечи в положении равновесия одинаковы: идентич­ные изменения сопротивлений в двух смежных плечах не приво­дят к разбалансу моста. Данное свойство позволяет компенси­ровать воздействия на результаты измерений влияющих вели­чин, в том числе температурных изменений сопротивлений под­водящих проводов (трехпроводная схема).

Для этой цели используют два датчика, на один из которых воздействуют как измеряемая, так и влияющая величавы, а второй, компенсационный, идентичный первому, подвергается воздействию только влияющей величины. Пусть — сопротивление измерительного датчика, причем 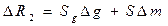, где S_g и S — чувствительности к влияющей и изме­ряемой величинам соответственно, определяемые как в разд. 3.2.1; R₁ — сопротивление компенсационного датчика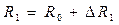 -постоянные сопротивле­ния, равные R₀. В этом случае выходное напряжение разбаланса

Как видно из формулы, v_m не зависит от влияющей величи­ны g.

Чувствительность схемы может быть удвоена, если поместить одинаковые датчики в двух противолежащих ветвях:

и два идентичных компенсационных датчика в двух остальных плечах:

Напряжение разбаланса в этом случае определяется как

Дифференциальное включение датчиков. Если плечи моста образованы из четырех одинаковых датчиков, изменения сопро­тивлений которых в смежных плечах попарно противополож­ны,

то напряжение разбаланса строго линейно зависит от измене­ний этих сопротивлений:

и при

 

Если два плеча моста образованы резисторами с постоян­ными сопротивлениями R₀=R₃=R₄, а два других плеча содер­жат идентичные датчики, изменения сопротивлений которых равны и противоположны по знаку, т. е.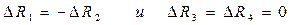

 

(последовательно-симметричный мост), то напряжение его раз­баланса

 

Если применяемые датчики имеют нелинейные характери­стики, то равные по величине и противоположные по знаку при­ращения измеряемой величины уже не вызовут равных по ве­личине и противоположных по знаку изменений сопротивлений датчиков. Рассмотрим последовательно-симметричный мост, в котором оба датчика имеют квадратичную характеристику. Датчик с сопротивлением R₂ воспринимает приращение из­меряемой величины, вызывающее изменение его сопротивления , причем

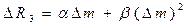
Воздействие на датчик с сопротивлением R₁ приращения измеряемой величины вызывает приращение

Напряжение разбаланса при использовании линейных дат­чиков, определяющееся выражением

для этого частного случая запишется в виде

Или, если выполняется обычно легко выполняемое условие

Напряжение разбаланса является квазилинейной функцией при­ращений измеряемой величины. Таким образом, дифференци­альное включение датчиков позволяет линеаризовать характе­ристику преобразования мостовой схемы даже в случаях не­линейности характеристик датчиков. Однако при воздействии влияющих величии на дифференциально включенные датчики полная компенсация этих воздействий оказывается невозможной. В этом случае для схемы моста с четырьмя идентичным датчиками имеем

и общее выражение для v_m приводится к виду

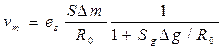
Напряжение v_m пропорционально изменениям только изме­ряемой величины, но чувствительность S_а схемы ( ) зависит от влияющей величины g из-за непостоянства чувстви­тельности Sg датчика при воздействии величины g.

Чаще всего влияющей величиной является температура; при этом , где T₀ —температура при равновесии моста, когда сопротивление каждого датчика равно R₀, температурный коэффициент сопротивле­ния датчика. В этом случае напряжение разбаланса

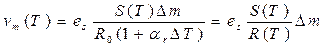
Минимизировать влияние температуры T на чувствительность схемы можно, включив последовательно с источником питания температурно-зависимые резисторы с сопротивлением R_S/2, ва­риации которых с температурой изменяют напряжение питания V моста таким образом, что чувствительность всей схемы оста­ется постоянной (рис. 3.15,а). Бели пренебречь сопротивлением источника, то, в соответствии с изложенным в разд. 3.3.1, напря­жение v_m будет определяться выражением

После преобразований получим

где R_экв — эквивалентное сопротивление моста,

Для схемы моста с четырьмя датчиками, включенными попар­но дифференциально, имеем

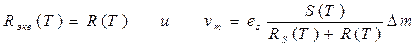
Если в диапазоне температур, в которых используется схема, тепловые вариации вызывают квазилинейные изменения сопро­тивлений

то напряжение v_m не зависит от T при условии

 

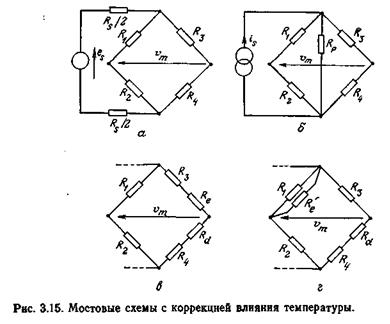
При питании моста источником тока влияние температурных изменений компенсируют температурно-зависимым резистором с сопротивлением R_P, включаемым в параллель диагонали с ис­точником питания (рис. 3.15,б).

.Менее точную компенсацию обеспечивает включение резисто­ров R_s и R_p, сопротивления которых не зависят от температуры.

Сопротивления выбирают такими, чтобы чувствительность схемы не изменялась в заданном температурном диапазоне.

Статические (в отсутствие внешних воздействий) сопротив­ления датчиков в четырех плечах моста, так же, как их темпе­ратурные коэффициенты, никогда не оказываются строго иден­тичными. Поэтому даже в отсутствие измеряемой величины наблюдается отличное от нуля напряжение разбаланса, изме­няющееся в функции температуры, которое именуют как сдвиг (или дрейф) нуля. Когда измеряемая величина изменяется, этот сдвиг алгебраически суммируется с напряжением разба­ланса, обусловленным воздействием измеряемой величины.

Коррекция дрейфа нуля, в том числе обусловленного темпе­ратурой, осуществляется с помощью двух резисторов, включае­мых в два плеча моста (рис. 3.15,в и г):

а) резистор с сопротивлением Rd, зависящим от Т, включа­ют последовательно, и его температурные отклонения противо­положны по знаку рабочим отклонениям температур;

б) резистор с сопротивлением R_e, не зависящим от темпера­туры, включаемый последовательно, или резистор R_е', включае­мый параллельно, предназначены для начального уравновеши­вания моста при температуре T₀.

Более простой, но менее точный способ коррекции состоит в использовании двух постоянных резисторов R_e и Rd, их сопро­тивления выбираются такими, чтобы скомпенсировать сдвиг нуля при температурах Т₁ и Т₂, представляющих собой грани­цы рабочего температурного диапазона.

Линеаризация характеристики преобразования мостовой схе­мы выбором потенциометричскго соотношения плеч. Мост строят, выбирая для каждого из образующих его ветви потен­циометров соотношение сопротивлений М>l. В состоянии рав­новесия схем

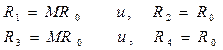
Если сопротивление датчика, скажем R₂, изменяется на , то измерительное напряжение разбаланса

По сравнению с равноплечим мостом, где M=1, член соотноше­ния, характеризующий нелинейность, уменьшился в (M+1)/2 раз; что же касается чувствительности, то она умень­шилась в (M+l)²/4M раз. Компенсацию воздействия влияющей величины можно осуществить включением компенсационного датчика с сопротивлением R₄, идентичного измерительному дат­чику с сопротивлением R₂ в этой ветви.

Устранение влияния соединительных проводов. Когда датчик расположен на значительном расстоянии от мостовой схемы, то его подключают к ней двумя проводами, сопротивлениями R_f которых нельзя пренебречь по сравнению с сопротивлением R_c датчика. При первоначальном (до начала измерений) уравнове­шивании моста проблем не возникает. Однако, так как оба про­вода составляют часть той же ветви моста, что и датчик, ва­риации их сопротивления ДД, обусловленные, например, изме­нением температуры, накладываются на приращения AR_C дат­чика, что приводит к погрешности измерений.

Чтобы напряжение разбаланса моста оставалось с точно­стью до малых второго порядка независимым от вариаций сопротивления соединительных проводов, датчик к мосту под­ключают через три одинаковых провода, с равными сопротив­лениями Rf, н располагают их один относительно другого так, чтобы вариации AR/ были одинаковы. При этом каждый провод включают в смежные ветви моста, с тем чтобы вариации сопро­тивления проводов были противоположны изменениям напряжения разбаланса.

При трехпроводной схеме включения датчика в мост третий провод подключают либо к источнику (рис. 3.16,а), либо к из­мерителю напряжения разбаланса (рис. 3.16, б).

В обоих случаях в равновесном состоянии

причем R₁ =R₂= R₃= R₄. Здесь R_c — сопротивление датчика.

В первой из схем (рис. 3.16, а) паразитная э.д.с. е_р самоин­дукции, наводимая в проводе, прибавляется к э.д.с. е_s источни­ка. Она не изменяет равновесия моста и не создает существен­ных помех измерениям при условии e_p<e_s.

Однако сопротивление Rf' провода прибавляется к сопротив­лению R_s, источника R_f'=Rs+Rf' что может привести к сниже­нию чувствительности моста, если R_s' не будет пренебрежимо мало по сравнению с R₀ (см. выше). Поэтому R_f' должно быть как можно меньшим, что достигается применением медных про­водов.

Во второй схеме (рис. 3.16,6) сопротивление R_f' обычно ма­ло по сравнению с входным сопротивлением измерительного прибора R_d, и при этом условии третий провод не влияет на чувствительность моста.

 

Однако паразитная эд.с е_р самоиндукции в проводе создает на нем напряжение, которое прибавляется к измеряемому на­пряжению v_m разбаланса и создает погрешность измерений, если е_Р не слишком мало по сравнению с v_m. По этой причине третий провод предпочитают присоединять к источнику питания либо используют компенсационную схему с двумя парами соеди­нительных проводов (рис. З.17). В последней датчик и два про­вода образуют плечо моста .R₂=R_c+2R_f.

Другое плечо —R₄ — состоит из постоянного сопротивления Ro" и двух одинаковых проводов, расположенных рядом друг с другом, при этом R₄= Ro"+2R_f В равновесном состоянии со­противления плеч моста выбирают равными друг другу, и из­менения Д/?(сопротивлений всех соединительных проводов с точностью до малых второго порядка не влияют на v_m.

В схеме с тремя соединительными проводами сопротивление датчика точно известно только в случае, когда сопротивления проводов Rf и их вариации абсолютно идентичны. В этом слу­чае значение входной измеряемой величины можно определить так называемым нулевым методом путем уравновешивания моста либо по напряжению разбаланса v_m при нарушении ус­ловия равновесия.

 

 

 

Скомпенсировать влияние соединительных проводов незави­симо от их параметров можно при четырехпроводном включе­нии датчика с использованием нулевого метода. Эта схема по­казана на рис. 3.18. Значение сопротивления R_c определяется по двум последовательным уравновешиваниям моста при двух

различных включениях проводов. При первом уравновешивании концы проводов соединяют согласно следующей маркировке:

А к а, D к f, F к b.

Мост уравновешивают с помощью резистора R₁, переменное со­противление которого в положении равновесия равно R₁', так что

При втором уравновешивании моста концы проводов пере­ключают следующим образом:

А к f, D к a, F к е.

Новое положение равновесия моста достигается при значении сопротивления R₁= R₁ '' причем

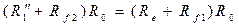
Сопротивление R_c датчика вычисляют по результатам двух уравновешиваний схемы как

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: