 |
Измерение импеданса датчиков и его параметров
|
|
|
|
Для измерения импеданса датчиков и его параметров—активного и реактивных сопротивлений и соответственно R, L и С —используют мосты переменного тока.
Электрическую схему замещения датчика, характеризуемого импедансом, можно представить двухполюсником с последовательным или параллельным соединением активного и реактивных сопротивлений, как это показано на рис 3.19. Основные соотношения, которыми характеризуются двухполюсники, приведены на рис. 3.19,а и 3.19,6. Та или иная схема замещения выбирается в зависимости от вида рассеиваемой (теряемой) мощности «а элементах двухполюсника. Если эти потери пропорциональны квадрату протекающего через двухполюсник тока I, что имеет место при наличии преобладающего активного сопротивления провода катушки индуктивности или утечки тока через конденсатор, т. е. теряется активная мощность на нагрев катушки или конденсатора, то датчик замещают последовательными схемами. Если потери пропорциональны квадрату напряжения на двухполюснике, что имеет место в случае диэлектрических потерь в конденсаторе или большой индуктивности катушки (потери реактивной мощности), то выбирают параллельную схему замещения.

|
Измерение параметров емкостного датчика. Диэлектрические потерн в конденсаторе можно представить резистором с сопротивлением Rc включенным параллельно с конденсатором емкостью Сc.
Принципиальная схема измерений с емкостным датчиком представляет собой так называемый мост Нернста (рис 3.20). Импеданс датчика равен
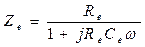
импеданс уравновешивающего плеча определяется выражением
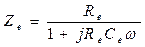
Условие равновесия моста:  , т.е.
, т.е. 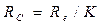 н
н  . Мост уравновешивают при значении измеряемой величины то, принимаемом за начальное. Когда т0 изменяется на
. Мост уравновешивают при значении измеряемой величины то, принимаемом за начальное. Когда т0 изменяется на  , импеданс датчика
, импеданс датчика
|
|
|
меняется от Zco до  . Тогда между точками А и В в диагонали моста появляется напряжение разбаланса
. Тогда между точками А и В в диагонали моста появляется напряжение разбаланса

и если  , то с точностью до малых второго порядка
, то с точностью до малых второго порядка


|
Выбирая. K=1, получают максимальную чувствительность схемы. Кроме того, благодаря симметрии моста легче скомпенсировать воздействие влияющих величин. При этих условиях

Если датчик представляет собой конденсатор с воздушным диэлектриком, то потери пренебрежимо малы, и импеданс датчика носит емкостной характер. В этом случае резистор Rе для уравновешивания моста можно не использовать. В таком мосте, известном как мост Саути (рис. 3.21), напряжение разбаланса равно

Мост уравновешивают при значении то, принимаемом за начальное значение измеряемой величины,, и устанавливают Се= Ссо. Тогда при 

Если  с точностью до малых
с точностью до малых
второго порядка.

|
Обкладки конденсаторов образуют с массой паразитные емкости, распределенные как показано на рис. 3.21,6. Эти паразитные конденсаторы параллельны каждому из резисторов R и входному импедансу измерительного прибора с активным сопротивлением Rd. Их воздействие на плечи моста можно сделать пренебрежимо малым выбором весьма малых сопротивлений R (102--103 Ом) по сравнению с паразитным емкостным сопротивлением. Более удобным является включение параллельно каждому резистору конденсатора небольшой емкости, что позволяет уравновесить мост компенсацией паразитных емкостей.
Паразитное емкостное сопротивление, параллельное входной цепи измерительного прибора, не влияет на равновесие моста, но оно может влиять на чувствительность схемы к разбалансу, если это паразитное емкостное сопротивление не слишком велико по сравнению со входным импедансом измерительного прибора. В этом случае более разумно проводить измерение тока разбаланса, используя измерительный прибор с входным импедансом, намного меньшим, чем подключенное ему в параллель паразитное емкостное сопротивление.
|
|
|
Ток разбаланса моста Саути, когда входной импеданс измерительного прибора пренебрежимо мал, определяется выражением

В легко реализуемом случае, когда 
при замене.

Измерение параметров индуктивного датчика. В зависимости от того, как лучше представить потери в катушке датчика — последовательным или параллельным сопротивлением соответствующей схемы замещения, используют соответственно мост Максвелла (рис. 3.22, а) или мост Гэя (рис. 3.22,б).
Условие равновесия для обеих мостовых схем одно и то же:

Для моста Максвелла

а для моста Гэя


Сопротивление и индуктивность датчика в функция значений параметров элементов моста определяются в обеих мостовых схемах как

Напряжение разбаланса в обеих схемах определяется выражением

и если \Z\<<\KR+Zco\, то с точностью до малых второго порядка

Чувствительность указанных мостовых схем максимальна при |Zc0|=KR,и, принимая.K=1 и R=|Zc0|, получим

Если выбрать KR>>|Zc0|, то

Если два датчика с одинаковыми статическими импедансами помещаются в смежные ветви моста, образуя дифференциальную схему, то в результате обеспечивается компенсация воздействия влияющих величин. И так как вариации измеряемой величины вызывают идентичные по значениям, но противоположные по знаку реакции датчиков, то достигаются улучшение линейности характеристики преобразования схемы в целом и линеаризация совокупной характеристики датчиков в частности.

|
Принципиальные схемы мостов с дифференциальным включением индуктивных датчиков приведены на рис. 3.23. Напряжение разбаланса в функции импедансов датчиков Zc1 и Zc2 выражается соотношением

Tax как при воздействии измеряемой величины 
и  ТО
ТО

Когда влияющая величина вызывает одинаковые изменения импедаисов Zc1, и Zc2, а измеряемая величина — им взаимообратные, то можно записать, что

где Sg —- чувствительность к влияющей величине, а S —чувствительность к измеряемой величине. С учетом этого предыдущее выражение для напряжения разбаланса можно записать в виде
|
|
|

Таким образом, напряжение разбаланса есть линейная функция приращений измеряемой величины; при этом воздействие влияющей величины уменьшено. Если приращения импеданса датчика, вызванные влияющей величиной, малы по сравнению со статическим импедансом Zc0, что обычно имеет место, то

В случае, когда характеристики датчиков нелинейны и нелинейность, к примеру, квадратичная, равные и противоположно направленные воздействия измеряемой величины вызывают изменения импедансов датчиков, которые уже не являются одинаковыми по величине и противоположными по знаку, т. е.

Напряжение разбаланса в этом случае выражается нелинейным соотношением

Которое, приводится к линейному виду

если  , что обычно имеет место.
, что обычно имеет место.
|
|
|


