 |
Передаточная функция ЧП. Интегрирующая цепь.
|
|
|
|
Вывод уравнений четырёхполюсника в «А» форме
Четырехполюсником называется часть электрической цепи или схемы, содержащая два входных вывода (полюса) для подключения источника энергии и два выходных вывода для подключения нагрузки.
где Y11, Y22 – входные проводимости входа и выхода, Y12 = Y21 – взаимная проводимость между входом и выходом.
Выразим из полученных уравнений режимные параметры на входе:
С учетом принятых обозначений система основных уравнений четырехполюсника получит вид:
A•D - B•C=1 – уравнение связи между коэффициентами.
Обратное включение четырёхполюсника
Уравнение для обратного включения можно получить из уравнений прямого включения с заменой 
Тогда уравнение примет вид
Приведем эти уравнения к структуре уравнений для прямого включения. Решим для этого уравнение относительно U1 и I1.
Тогда для симметричного ЧП следует, что А=D.
Определение коэффициентов ЧП расчетным путем
Существует 2 пути определения коэффициента:
1) Расчетный
2) Опытный
Один из основных путей определения коэффициентов ЧП вытекает из режимов ХХ и КЗ. Из системы равнений в «А» форме следует, что 
,отсюда 
Рассмотрим схему
Режим ХХ
Опыт КЗ:
Для проверки правильность расчетов обычно используют уравнения связи.
Опытное определение коэффициентов ЧП
Структура схемы неизвестна. Комплексные входные сопротивления ЧП могут быть определены опытным путем с помощью вольтметра, амперметра и ваттметра.
Из уравнений ЧП в «А» форме следует, что комплексные входные сопротивления в режимах ХХ и КЗ равны
Из опыта обратного включ.
; 
AD-BC=1 – уравнение связи
Считая Z1xx, Z2xx и Z2кз известными находим коэффициенты: (справа от скобки)
|
|
|
Вторичные (характеристические) параметры ЧП
В электросвязи широко используется режим работы симметр. ЧП при котором его входное сопротивление равно нагрузочному, т.е. характеристическое уравнение 
Режим работы ЧП для которого справедливо ZC=ZВХ=ZH называется режимом согласованной нагрузки. В указанном режиме для симметричного ЧП можно записать
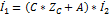
Коэффициент передачи симметричного ЧП
Рассмотрим отношение входного напряжения Чп к выходному, а так же входного тока к выходному:
С учетом того, что А=D
g- коэффициент передачи ЧП (комплек)
показывает во сколько раз ослабляется величина тока (напряжения) при прохождении сигнала через ЧП. Затухание 1Нп соответствует ослабление величины передаваемого тока (напряжения) в е раз.
характеризует как изменяется фаза передаваемая через ЧП тока или напряжения.
Передаточная функция ЧП. Диффер-щая цепь
Пусть на входе ЧП действует ток (напряжение) х1(t), а на выходе х2(t). Задача описать ЧП для всех режимов его работы. Для решения этой задачи используют понятия передаточной функции. Перед.функция- это отношение изображений по Лапласу выходного воздействия к входному при нулевых начальных условиях.
вместо х либо токи, либо напряжения
Рассмотрим применение понятия передаточной функции к анализу диф-щей. цепи.
Считаем, что сопротивление нагрузки стремится к 
(режим ХХ)
Второй закон Кирхгофа в опер.виде:
Рассматривая
Это передаточная функция реальной диф цепи
Рассмотрим перед. функцию идеальной диф цепи
Для такой цепи выполняется
В период Т при импульсном сигнале на входе можно принять как tu, тогда rc<<tu. Таким образом, цепь хорошо диф-ет, если ее постоянная времени намного меньше длительности воздействующегося импульса
При rcp<<1=>k(p)=rcp т.е.
Передаточная функция ЧП. Интегрирующая цепь.
|
|
|
Пусть на входе ЧП действует ток (напряжение) х1(t), а на выходе х2(t). Задача описать ЧП для всех режимов его работы. Для решения этой задачи используют понятия передаточной функции. Перед.функция- это отношение изображений по Лапласу выходного воздействия к входному при нулевых начальных условиях.
вместо х либо токи, либо напряжения
Рассмотрим применение понятия передаточной функции к анализу интегр. цепи.
Сопротивление нагрузки стремится
к . U1=I(p)(r+1/cp); U2=I(p)1/cp
реал.ин
Идеальную интегр. цепь получим при rcp>>1 или при rc>>tu, тогда перед. функция идеал.интегр.цепи k(p)=1/rcp
Следовательно U2(p)=U1(p)*1/rcp, тогда оригинал
то есть цепь интегрирует
|
|
|
