Выбор мощности двигателя электропривода

 

Правильный выбор мощности электродвигателя для привода должен удовлетворять требованиям экономичности, производительности и надежности рабочей машины. Установка двигателя большей мощности, чем это необходимо по условиям привода, вызывает излишние потери энергии при работе машины, обусловливает дополнительные капитальные вложения и увеличение габаритов двигателя. Установка двигателя недостаточной мощности снижает производительность рабочей машины и делает ее работу ненадежной, а сам электродвигатель в подобных условиях легко может быть поврежден.

Двигатель должен быть выбран так, чтобы его мощность использовалась возможно полнее. Во время работы двигатель должен нагреваться примерно до предельно допустимой температуры, но не выше ее. Кроме того, двигатель должен нормально работать при возможных временных перегрузках и развивать пусковой момент, требуемый данной рабочей машиной. В соответствии с этим мощность двигателя выбирается в большинстве случаев на основании условий нагревания (выбор мощности по нагреву), а затем производится проверка соответствия перегрузочной способности двигателя условиям пуска машины и временным перегрузкам. Иногда (при большой кратковременной перегрузке) приходится выбирать двигатель, исходя из требуемой максимальной мощности. В подобных условиях длительная мощность двигателя часто полностью не используется.

Выбор мощности двигателя для привода с продолжительным режимом работы при постоянной или мало изменяющейся нагрузке на валу является простым. В этих условиях мощность двигателя должна быть равна мощности нагрузки, а проверки на нагрев и перегрузку во время работы не нужны. Однако необходимо проверить, достаточен ли пусковой момент двигателя для пусковых условий данной машины.

Мощность продолжительной нагрузки ряда хорошо изученных механизмов определяется на основании проверенных практикой теоретических расчетов.

Например, мощность двигателя (Р, кВт) для вентилятора

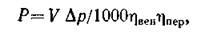
где V — количество нагнетаемого или всасываемого воздуха, м³/с; ∆р — перепад, Па;η_вен —КПД вентилятора (у крыльчатых вентиляторов 0,2—0,35, у центробежных — до 0,8); η_пер — КПД передачи от двигателя к вентилятору.

В приведенной формуле произведение V ∆р представляет собой полезную мощность вентилятора, а 1000 — коэффициент для перевода мощности в киловатты.

Во многих случаях для расчета мощности двигателя приводов для продолжительного режима используются эмпирические формулы, проверенные длительной практикой.

Для малоизученных приводов продолжительной нагрузки мощность двигателя часто определяется на основании удельного расхода энергии при выпуске продукции или экспериментально путем испытания привода.

Выбор мощности двигателя при кратковременном и повторно-кратковременном режимах работы. При кратковременном, повторно-кратковременном и продолжительном с переменной нагрузкой режимах важно знать закон изменения во времени превышения температуры υ двигателя над температурой окружающей среды. Электрическая машина с точки зрения нагревания представляет собой весьма сложное тело. Тем не менее, при расчетах, не требующих большой точности, можно считать электрическую машину однородным телом.

Это дает возможность применить к ней упрощенное уравнение нагревания

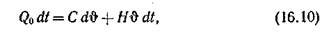
где С — теплоемкость машины; Н — ее теплоотдача; Q_o— теплота, выделяющаяся в машине в единицу времени.

Далее, при 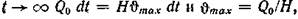на основании чего

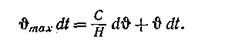
Решая это уравнение методом разделения переменных, получаем:

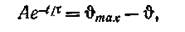
где τ = С/Н — постоянная времени нагрева машины, определяемая экспериментально.

При t = 0 начальное превышение температуры υ =υ ₀, на основании чего постоянная А = υ _тах - υ ₀, а закон нарастания превышения температуры машины будет иметь вид:

Таким образом, в данном случае, как и при υ ₀ = 0, превышение температуры возрастает по показательному закону, стремясь к значению υ _max. Значение начального превышения температуры лишь изменяет скорость изменения температуры, не изменяя характера процесса (рис. 16.5).

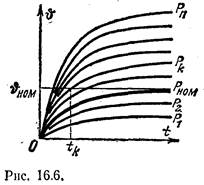При различных значениях продолжительной нагрузки одной и той же машины графики υ (t) будут отличаться лишь ординатами {рис. 16.6). Наибольшее допустимое для данной машины превышение температуры равно υ_ном- Прямая, параллельная оси абсцисс, υ = = υ_мом, пересекаете различных точках кривые υ (t), соответствующие различным значениям нагрузки электродвигателя.

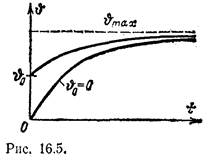Абсцисса точки пересечения определяет тот промежуток времени t_к,- в течение которого мощность двигателя может быть временно равна мощности P_k, представляющей собой перегрузку по отношению к его номинальной мощности в продолжительном режиме. График нагревания, асимптотически приближающийся к υ_ном. соответствует номинальной мощности двигателя Р_ном. При нагрузках, меньших Р_ном, мощность двигателя полностью не используется. Однако если двигатель загружается до номинальной мощности только на относительно короткое время, то по существу он тоже используется не полностью. Целесообразно его кратковременно перегрузить, и чем меньше продолжительность работы, тем больше должна быть эта перегрузка. Предел повышения нагрузки двигателя по мере уменьшения продолжительности включения определяется мгновенной перегрузочной мощностью двигателя, зависящей от его • электрических свойств (максимального момента у асинхронного двигателя, условий коммутации у машин постоянного тока и т. п.). При повторно-кратковременном режиме двигатель попеременно то нагревается, то охлаждается. Изменение его температуры в течение времени каждого цикла зависит при этом от предыдущего теплового состояния.

График зависимости нагревания и охлаждения машины от времени в подобных условиях показан на рис. 16.7. Конечное превышение температуры каждой данной части цикла является начальным превышением температуры для последующей части цикла. Если во время той или иной части цикла наступает значительное изменение условий охлаждения (остановка двигателя или заметное изменение частоты вращения), то это изменяет τ = С/Н — постоянную времени нагрева двигателя, что должно быть учтено при построении графиков.

Определение мощности двигателя по условиям нагревания посредством построения графиков нагревания (или соответствующим аналитическим методом) требует значительной затраты времени и не дает точных результатов. Здесь эти построения приведены лишь, чтобы наглядно показать картину изменения нагрева двигателя при переменной нагрузке. В большинстве случаев для такого выбора мощности двигателя применяются более простые методы, в частности эквивалентного тока.

В основу метода эквивалентного тока положено допущение, что при переменной нагрузке двигателя его средние потери должны быть равны потерям при продолжительной (номинальной) нагрузке. Как известно, мощность потерь двигателя складывается из постоянных Р_пост и переменных Р_пер мощностей. Мощность постоянных потерь равна сумме мощности потерь на трение, в магнитопроводе (у асинхронных двигателей и двигателей постоянного тока с параллельным возбуждением), на возбуждение у синхронных двигателей и двигателей с параллельным возбуждением. Мощность переменных потерь можно считать пропорциональной квадрату рабочего тока I двигателя и сопротивлению соответствующей обмотки r, причем приближенно можно считать последнее постоянным. Если ток изменяется за соответствующие промежутки времени, то за все рабочее время I>t = Т суммарные потери энергии в двигателе будут:

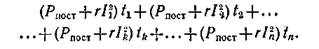
При эквивалентной неизменной нагрузке током I_эк за то же время Т потери энергии в двигателе должны быть равны:

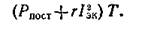
Нагревание двигателя, обусловленное потерями, в обоих случаях должно быть одинаковым. На этом основании определяем эквивалентный ток:

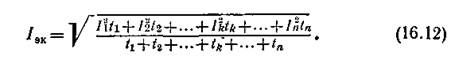
Зная эквивалентный ток, номинальное напряжение и номинальный коэффициент мощности, можно определить номинальную мощность двигателя:

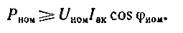
Метод эквивалентного тока можно применять лишь при условии постоянства мощности потерь в магнитопроводе и на трение, а также сопротивлений обмоток в течение всего рабочего времени. Такому условию, например, не удовлетворяет двигатель с последовательным возбуждением, у которого при изменениях нагрузки сильно изменяются поток и частота вращения (следовательно, мощность потерь в стали магнитопровода и на трение).

В ряде случаев условия нагрузки определяют непосредственно момент, требуемый от двигателя, а не ток. В этих случаях можно пользоваться методом эквивалентного момента: у всех электродвигателей вращающий момент пропорционален произведению тока и потока. У двигателей переменного тока можно приближенно считать постоянным коэффициент мощности. Наконец, магнитный поток можно считать практически постоянным у всех двигателей, кроме двигателей с последовательным и смешанным возбуждением. При таких упрощениях можно считать вращающий момент где k_вp — постоянная величина,

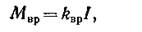откуда из (16.12) следует:

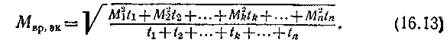
По эквивалентному моменту и номинальной угловой скорости двигателя о>_ном рассчитывается номинальная мощность двигателя Р_ном = М_вр,эк ω _ном

Выбрав номинальную мощность двигателя на основании расчета по методу эквивалентного тока или эквивалентного момента, необходимо затем проверить, достаточен ли максимальный момент М_тах двигателя для того, чтобы удовлетворить требованиям кратковременных перегрузок данного привода; иными словами, должно быть выполнено условие: коэффициент перегрузки двигателя λ_мом должен быть больше отношения максимального момента М_тах нагрузки к номинальному моменту двигателя, т. е.

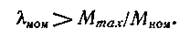
⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: