 |
Изучение гармонических колебаний пружинного и математического маятников
|
|
|
|
ЛАБОРАТОРНАЯ РАБОТА № 2
Введение
Цель работы: изучение гармонических колебаний на примере пружинного и математического маятников.
Приборы и принадлежности: лабораторные установки пружинного и математического маятников, секундомер.
Колебаниями называют такие движения или изменения состояния физической системы, при которых система неоднократно возвращается в исходное состояние, например, в состояние равновесия.
Колебательные движения широко распространены в природе. Это волнение на море, колебания струн, вибрации фундаментов зданий, колебания маятника часов - примеры можно было бы продолжать до бесконечности. Разнообразные по природе колебания могут иметь общие закономерности, описываться однотипными математическими методами. Такая общность составляет основу для изучения самых различных колебаний, встречающихся в разнообразных физических явлениях и технических устройствах.
Колебательные процессы, с которыми приходится встречаться, подразделяютнапериодические и непериодические в зависимости от характера изменения со временем физических величин, характеризующих состояние системы. По причине своего возникновения колебания подразделяют на свободные и вынужденные.
Свободными (собственными) колебаниями называются колебания, которые возникают в системе в результате однократного начального выведения ееиз состояния устойчивого равновесия. При свободных колебаниях в системе всегда действуют силы (в общем случае причины), стремящиеся возвратить систему в положение равновесия. ( В случае колебания груза на пружине возвращающей силой будет сила упругости пружины.)
Еслив системе отсутствуют силы трения и любые другие причины, препятствующие свободным колебаниям, то нет потерь механической энергии, и колебания могут происходить сколь угодно долго с постоянной амплитудой. Такие свободные колебания называются незатухающими. Незатухающие колебания представляют идеализированный случай колебаний. Свободные колебания реальных систем всегда затухающие. Затухание колебаний связано, главным образом, с действием в системе сил трения. Незатухающие колебания в реальной системе могут возбуждаться воздействием на нее переменной внешней силы. В этом случае колебания называются вынужденными.
|
|
|
Периодическими называют колебания, при которых значения всех физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени. Наименьший такой промежуток времени 
, по истечении, которого повторяются значения всех величин, характеризующих колебательное движение, называется периодом колебаний. За это время, говорят, совершается одно колебание.
Частотой 
периодических колебанийназывают число колебаний в единицу времени.Если за время 
система совершает 
колебаний,то частота колебаний равна: 
. Учитывая, что за время, равное периоду 
совершается одно колебание 
, приходим к связи частоты с периодом :
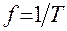
Частоту измеряют в герцах (Гц). За 1 Гц принимают частоту такого колебательного процесса, при котором за одну секунду совершается одно полное колебание (Гц=1/с).
Частным случаем периодических колебаний являются гармонические колебания, в которых колеблющаяся физическая величина 
(например, координата груза на пружине) изменяется со временем по закону косинуса (или синуса):
, (1)
где величина 
, равная наибольшему абсолютному значению колеблющейся величины 
, называются амплитудой колебаний. Выражение 
определяет значение в любой момент времени и называется фазой колебания. В начальный момент времени 
фаза 
равна начальной фазе 
.
|
|
|
Величину 
называют циклической частотой гармонического колебания.
Периодом функции (1), как известно из математики, является
- это и будет период колебаний. Для частоты гармонического колебания имеем:
.
Заметим, что функция (1) является решением дифференциального уравнения:
, (2)
где 
- вторая производная функции 
по времени.
В самом деле:
;
и при подстановке в уравнение (2) оно обращается в верное равенство, что и требовалось доказать.
В математике доказывается,что функция (1) является единственным решением дифференциального уравнения (2). Таким образом, если при колебаниях для колеблющейся физической величины в любой момент времени имеет место соотношение (2), то колебания являются гармоническими и происходят с периодом
.
Значения постоянных и определяются, как правило, из начальных условий.
В лабораторной работе 2 Вам предстоит экспериментально исследовать свободные колебания пружинного и математического маятников.
|
|
|
12 |
