 |
Геометрическая интерпретация стандартной задачи линейного программирования
|
|
|
|
Специфические особенности ЗЛП (линейная целевая функция, линейные ограничения) позволяют получить ряд геометрических интерпретаций, связанных с поиском ее решения.
2.1 Задача планирования товарооборота
При продаже товаров А и В используется три вида ресурсов: R1, R2, R3 (например, R1 - рабочее время; R2 - полезная площадь торгового зала; R3 - упаковочный материал). Сведения о количестве ресурсов, необходимых для продажи единицы каждого товара, обеспеченности торгового предприятия этими ресурсами и ценах, по которым товары продаются, приведены в следующей таблице:
Таблица 3
| Ресурсы | Товары | Запас ресурсов | |
| A | B | ||
| R1 | 2 | 3 | 19 |
| R2 | 2 | 1 | 13 |
| R3 | 0 | 3 | 15 |
| Цена товара | 7 | 5 | |
Составим план продажи товаров, обеспечивающий максимальный товарооборот.
Для математической формализации оптимизационной проблемы воспользуемся сформулированном в предыдущем параграфе алгоритмом.
Укажем переменные, подлежащие определению в результате решения задачи, и введем понятие плана.
Обозначим через X1 и X2 запланированный объем продажи товаров А и В и назовем вектор X=(X1, X2) планом продажи товаров.
Составим уравнения и неравенства, определяющие множество допустимых планов.
Из экономического смысла величин X1 и X2 следует, что X1³0, X2³0.
Из таблицы 1 следует, что продажа X1 единиц товара А требует 2X1 единиц первого ресурса и 2X1 единиц второго ресурса, а продажа X2 единиц товара В требует 3X2 единиц первого ресурса, X2 единиц второго ресурса и 3X2 единиц третьего ресурса. Таким образом, план продажи X=(X1, X2) допустим, если для его реализации достаточно имеющихся в наличии ресурсов:
 (1) (1)
|
Построим целевую (критериальную) функцию
|
|
|
Из последней строчки таблицы 1 следует, что при реализации плана X=(X1, X2) товарооборот составит E(x)=7X1+5X2 денежных единиц.
Выпишем получившуюся математическую модель оптимизационной задачи или задачу математического программирования:
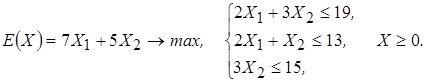 (2) (2)
|


Рис. 2 - Построение допустимого множества задачи планирования товарооборота
Изобразим на плоскости допустимое множество задачи (2). Учитывая неотрицательность оптимизируемых переменных, ограничимся первой четвертью декартовой прямоугольной системы координат OX1X2.
Последовательно изобразим планы, полностью исчерпывающие запас первого (отрезок I), второго (отрезок II) и третьего ресурса (отрезок III), а затем стрелками укажем те полуплоскости, в которых лежат планы, на которые соответствующего ресурса хватит с избытком. Допустимым множеством задачи (2) является пересечение вышеупомянутых полуплоскостей (множество планов, на реализацию которых хватит всех ресурсов) (рис. 1).
Определим, в какой точке допустимого множества задача (2) имеет решение. С этой целью рассмотрим множество поверхностей уровня целевой функции задачи (совокупность планов продажи товаров с одинаковым товарооборотом):
| E(x)=7X1+5X2=d, | (3) |
геометрически представляющих собой семейство отрезков параллельных прямых.
Изобразим некоторую поверхность уровня, соответствующую, например, d=14, которая представляет собой прямую, заданную уравнением:


7X1+5X2=14
Рис. 3 - Геометрическое решение СЗЛП
Стрелка на рис. 2 указывает направление, в котором лежат планы продаж с большим (чем 14) товарооборотом, в противоположном направлении лежат планы с меньшим товарооборотом.
Поскольку в направлении стрелки лежат допустимые планы задачи (2), можно добиться большего товарооборота, перемещая поверхность уровня параллельно самой себе до тех пор, пока она пересекает допустимое множество. План A (рис. 2) является планом с наибольшим товарооборотом, поскольку все отличные от A планы лежат ниже поверхности уровня, которому принадлежит план A.
|
|
|
Координаты точки А удовлетворяют уравнениям прямых, на пересечении которых она лежит. Решая систему

получаем оптимальное решение задачи: X*=(5, 3) (X1=5; X2=3). При этом товарооборот составит
Еmax=7´5 + 5´З = 50
денежных единиц.
Симплекс-метод
В настоящем параграфе рассмотрим алгоритм основного аналитического метода решения задач линейного программирования - симплекс-метода.
Симплекс-метод применяется только к канонической ЗЛП (1.9).
Приведем задачу планирования товарооборота к канонической форме. Введем дополнительные переменные:
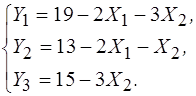 (1) (1)
|
Переменные Y1, Y2 и Y3 имеют очевидный экономический смысл - это остатки сырья R1, R2, R3 при реализации плана X=(X1, X2).
Алгоритм симплекс-метода, рассматриваемый в настоящих методических указаниях, применяется только к задаче минимизации.
Задачу нахождения максимума всегда можно свести к задаче нахождения минимума, сменив знак у целевой функции, причем:
обе задачи будут иметь одно и то же множество решений, значения задач будут различаться знаком.
Таким образом, задачу об отыскании максимума функции Е можно свести к задаче отыскания минимума функции Е' = -Е. Для единообразия схемы применения симплекс-метода мы будем говорить о нахождении только минимума функции. Поэтому задачу планирования товарооборота будем рассматривать как задачу минимизации функции
| Е' = -7X1-5X2 | (2) |
на множестве всех допустимых планов.
Итак, при решении симплекс-методом задачи планирования товарооборота используется следующая ее формулировка:
найти такие неотрицательные значения переменных X1, X2, Y1, Y2, Y3 (план Z=(X1, X2, Y1, Y2, Y3)), удовлетворяющие системе (1), при которых функция (2) достигает минимума.
В системе уравнений (1) переменные Y1, Y2, Y3 выражены через X1, X2. В соответствии с этим переменные Y1, Y2, Y3 называются базисными, а переменные X1, X2 - свободными.
Из геометрической интерпретации задачи следует, что оптимальное решение достигается в одной из вершин многоугольника области допустимых решений (ОДР). Вершины ОДР называются опорными точками, а соответствующие допустимые решения - опорными решениями задачи (опорными планами).
|
|
|
Идея симплекс-метода заключается в том, чтобы, переходя от одного опорного плана к другому, двигаться в направлении уменьшения значения минимизируемой функции.
При нахождении опорных планов следует иметь в виду следующее их свойство: в опорном плане обращаются в нуль по крайней мере столько переменных, сколько свободных переменных содержит система уравнений задачи.
Рассмотрим алгебраические основы симплекс-метода на примере задачи планирования товарооборота.
Решение задачи симплекс-методом начинается с нахождения первого опорного плана. Положив в (1) свободные переменные X1 и X2 равными нулю, получаем:
линейный программирование транспортный задача
X1=X2=0, Y1=19, Y2=13, Y3=15.
При этом Е' = Е = 0. Так как значения всех переменных неотрицательны, полученный план Z1=(0, 0, 19, 13, 15) является опорным. Согласно этому плану товары не продаются и товарооборот равен нулю. Естественно, такой план не может быть оптимальным.
Этот вывод следует и из формальных рассуждений: увеличивая любую из переменных X1 и X2 (что, очевидно, возможно), мы уменьшаем значение функции Е' = -7X1-5X2, так как эти переменные входят в выражение Е' с отрицательными коэффициентами.
Будем увеличивать X1, оставляя X2 = 0. Новый опорный план будет достигнут, как только одна из переменных Y1, Y2 или Y3 обратится в нуль. Из (1) имеем: Y1 = 0 при X1 = 19/2, Y2 = 0 при X1 = 13/2; Y3 =15 при любом значении X1. Таким образом, в новом опорном решении
= min{19/2, 13/2}=13/2,
при этом X2 = Y2 = 0.
Чтобы проверить, является ли новый опорный план оптимальным, нужно из уравнений (1) выразить переменные X1, Y1 и Y3 через X2 и Y2, а затем подставить полученное выражение X1 в функцию Е'. Таким образом, мы заменим в системе (1) свободную переменную X1 на бывшую базисную Y2.
Вместо того, чтобы переразрешать систему уравнений относительно новых базисных переменных, можно выполнить преобразование специальной таблицы, которая называется симплексной таблицей. Для ее составления следует записать систему уравнений задачи и целевую функцию в так называемой стандартной форме: в правых частях уравнений и в выражении целевой функции после свободных членов ставится знак (-) и далее в скобках записываются свободные переменные с соответствующими коэффициентами.
|
|
|
Запишем в стандартной форме нашу задачу:
 (3) (3)
|
По стандартной форме записи системы и целевой функции составляется симплексная таблица, в которую записываются свободные члены и коэффициенты при свободных переменных:
Таблица 4
| Базисные переменные | Свободный член | Свободные переменные | ||
| X1 | X2 | |||
| Y1 | 19 | 2 | 3 | 19/2 |
| Y2 | 13 | 2 | 1 | 13/2 |
| Y3 | 15 | 0 | 3 | - |
| Е' | 0 | 7 | 5 | |
Эта таблица соответствует первому опорному плану: свободные переменные X1 и X2 равны нулю, а базисные переменные Y1, Y2, Y3 и функция Е' равны соответствующим свободным членам.
План оптимален, если в столбцах свободных переменных в последней строке таблицы нет положительных коэффициентов.
Таким образом, рассматриваемый план не оптимален. Чтобы уменьшить функцию Е', следует увеличить свободную переменную, которой соответствует положительный коэффициент в строке Е' (например, X1). В новом опорном плане обратится в нуль та базисная переменная, для которой отношение свободного члена к соответствующему (положительному!) коэффициенту столбца X1 будет минимальным (эти отношения записываются в последнем столбце таблицы). В нашем примере это переменная Y2.
Для вычисления нового опорного плана следует в системе уравнений (1) заменить свободную переменную X1 на базисную Y2.
Соответствующая симплексная таблица (симплекс-таблица) будет иметь следующий вид:
Таблица 5
| Базисные переменные | Свободный член | Свободные переменные | |
| Y2 | X2 | ||
| Y1 | |||
| X1 | |||
| Y3 | |||
| Е' | |||
Чтобы определить коэффициенты, которые должны быть записаны в этой таблице, нужно преобразовать таблицу 1 в соответствии с приведенным ниже алгоритмом. При этом удобно вести расчеты прямо в исходной таблице, отводя левый верхний угол каждой клетки для исходных коэффициентов, а правый нижний - для вспомогательных результатов.
Алгоритм преобразования симплекс-таблицы
В исходной таблице (таблица 3) выделяются столбец и строка, соответствующие тем переменным, которые меняются местами. Они называются разрешающим столбцом и разрешающей строкой (в нашем примере это столбец X1 и строка Y2). Элемент, стоящий на их пересечении, называется разрешающим элементом.
Таблица 6
| Базисные переменные | Свободный член | Свободные переменные
| ||||||
|
| X1 | X2 | ||||||
| Y1 | 19 | 2 | 3 | |||||
| -13 | -1 | -1 | ||||||
| Y2 | 13 | 13/2 | 2 | 1 | 1/2 | |||
| 1/2 | ||||||||
| Y3 | 15 | 0 | 3 | |||||
| 0 | 0 | 0 | ||||||
| Е' | 0 | 7 | 5 | |||||
| -91/2 | -7/2 | -7/2 | ||||||
Вычисляется величина l, обратная к разрешающему элементу. Значение l записывается в правом нижнем углу той же клетки, в которой находится разрешающий элемент.
Каждый элемент разрешающей строки (кроме разрешающего элемента) умножается на l, результат записывается в правом нижнем углу той же клетки.
Каждый элемент разрешающего столбца (кроме разрешающего элемента) умножается на (-l), и результат записывается в правом нижнем углу той же клетки.
В разрешающей строке выделяются все старые элементы (кроме разрешающего). В разрешающем столбце выделяются все новые элементы, за исключением клетки с разрешающим элементом.
Для каждой из клеток, не принадлежащих ни к разрешающей строке, ни к разрешающему столбцу, в правый нижний угол записывается произведение выделенных чисел, стоящих в том же столбце и в той же строке, что и данная клетка.
Таблицу переписывают, при этом заменяют:
выделенную свободную переменную - на выделенную базисную;
элементы разрешающего столбца и разрешающей строки - на числа, стоящие в правых нижних углах клеток;
каждый из остальных элементов таблицы - на сумму чисел, стоящих в левом верхнем углу и в правом нижнем углу клетки.
Выполнив преобразование таблицы 3 в соответствии с приведенным алгоритмом, получим следующую таблицу:
Таблица 7
| Базисные переменные | Свободный член | Свободные переменные | |
| Y2 | X2 | ||
| Y1 | 6 | -1 | 2 |
| X1 | 13/2 | 1/2 | 1/2 |
| Y3 | 15 | 0 | 3 |
| Е' | -91/2 | -7/2 | 3/2 |
Этой таблице соответствует следующая запись системы уравнений и функции Е':
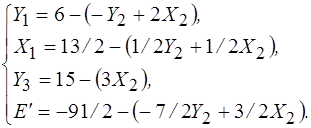
В новом опорном плане Z2=(13/2, 0, 6, 0, 15)
Y2=X2=0, Y1=6, X1=13/2, Y3=15, Е'= -91/2, Е = -Е'= 91/2.
Согласно этому плану, следует продавать 13/2 единиц товара А и не продавать товар В; при этом остатки ресурсов R1 и R3 равны, соответственно, 6 и 15 единицам, а ресурс R2 расходуется полностью. Товарооборот равен 91/2.
Этот план не оптимален, так как в последней строке таблицы есть положительный коэффициент при свободной переменной X2, а значит, увеличивая X2, можно уменьшить Е' (увеличить товарооборот). Выделим в таблице 7 разрешающий столбец X2. Минимальное из отношений свободных членов к положительным коэффициентам столбца X2 определяет в качестве разрешающей строки строку Y1.
Таблица 7
| Базисные переменные | Свободный член | Свободные переменные | ||||
|
| Y2 | X2 | ||||
| Y1 | 6 | -1 | 2 | |||
| 3 | -1/2 | 1/2 | ||||
| X1 | 13/2 | -3/2 | 1/2 | 1/2 | ||
| 1/4 | -1/4 | |||||
| Y3 | 15 | 0 | 3 | |||
| -9 | 3/2 | -3/2 | ||||
| Е' | -91/2 | -7/2 | 3/2 | |||
| -9/2 | 3/4 | -3/4 | ||||
Применив алгоритм преобразования симплекс-таблицы, получим следующую таблицу:
Таблица 8
| Базисные переменные | Свободный член | Свободные переменные | |
| Y2 | Y1 | ||
| X2 | 3 | -1/2 | 1/2 |
| X1 | 5 | 3/4 | -1/4 |
| Y3 | 6 | 3/2 | -3/2 |
| Е' | -50 | -11/4 | -3/4 |
Симплекс-таблице 6 соответствует опорный план Z3=(5, 3, 0, 0, 6)
= Y1 = 0, X2 = 3, X1 = 5, Y3 = 6,
и значение оптимизируемой функции Е' = - 50 (соответственно, Е = 50).
Полученный план оптимален, поскольку в последней строке таблицы 6 нет положительных коэффициентов в столбцах свободных переменных.
Таким образом, в рассматриваемой задаче оптимальным является следующий план: продавать 5 единиц товара А и 3 единицы товара В. При этом полностью расходуются ресурсы R1 и R2 и остаются неиспользованными 6 единиц ресурса R3. Такой план обеспечивает максимальный товарооборот, равный 50 рублям.
|
|
|


