 |
Алгоритм решения транспортной задачи
|
|
|
|
Определение опорного транспортного плана
Как и в общем случае, решение транспортной задачи начинается с нахождения первого опорного плана. Существует несколько методов построения опорного плана перевозок. Рассмотрим один из них - метод наименьшей стоимости.
При построении опорного плана этим методом сначала заполняется клетка таблицы с минимальной стоимостью. При этом на каждом шаге либо удовлетворяется спрос соответствующего магазина, либо исчерпывается запас базы. Далее клетки заполняются в порядке возрастания стоимостей.
Построение опорного плана перевозок
Условия транспортной задачи заданы транспортной таблицей 1:
Таблица 10
| Базы | Магазины | Запас | ||||||||
| B1 | B2 | B3 | A4 | |||||||
| A1 | 7 | 3 |
| 4 | 2 | 15 | ||||
| A2 | 6 | 1 |
| 4 | 6 | 31 | ||||
| A3 | 6 | 9 |
| 5 | 3 | 25 | ||||
| A4 | 10 | 4 | 7 | 9 | 22 | |||||
| Спрос | 28 | 17 | 28 | 20 | ||||||
Составим опорный план перевозок методом наименьшей стоимости.
Заполним таблицу 1, начиная с клетки (A2, B2), в которой мы имеем минимальную стоимость перевозки (c22 = 1). За счет запаса базы A2 можно удовлетворить всю заявку магазина B2, поэтому записываем 17 в клетку (A2, B2).
Следующую по величине стоимость, равную 2, имеем в клетке (A1, B4). Поскольку запас базы A1 меньше заявки магазина B4, в эту клетку записываем перевозку, равную запасу базы A1 (15 единиц). Следующую по величине стоимость равную 3, имеем в клетках (A1, B2) и (A3, B4). Клетку (A1, B2) нельзя заполнять, поскольку запас базы A1 уже исчерпан. Заполняем клетку (A3, B4), удовлетворяя оставшуюся часть заявки магазина B4 (5 единиц) за счет базы A3.
Рассуждая аналогично, заполняем остальные клетки в такой последовательности: (A2, B3), (A3, B3), (A3, B1), (A4, B1). Будем иметь:
|
|
|
Таблица 11
| Базы | Магазины | Запас | ||||||||
| B1 | B2 | B3 | A4 | |||||||
| A1 | 7 | 3 |
| 4 | 2 | 15 | ||||
|
| 15 | |||||||||
| A2 | 6 | 1 |
| 4 | 6 | 31 | ||||
| 17 | 14 | |||||||||
| A3 | 6 | 9 |
| 5 | 3 | 25 | ||||
| 6 | 14 | 5 | ||||||||
| A4 | 10 | 4 | 7 | 9 | 22 | |||||
| 22 |
| |||||||||
| Спрос | 28 | 17 | 28 | 20 | ||||||
Нетрудно убедиться в том, что сумма перевозок в каждой строке таблицы равна запасу товара на соответствующей базе, а в каждом столбце - заявке соответствующего магазина. Таким образом, мы получили план перевозок товара, удовлетворяющий всем ограничением транспортной задачи (перевозки по маршрутам, соответствующим незаполненным клеткам, полагаются равными нулю):
=(0, 0, 0, 15, 0, 17, 14, 0, 6, 0, 14, 5, 22, 0, 0, 0),
или, в матричной форме,

Вычислим стоимость плана x:
(x)=2´15+1´17+4´14+6´6+5´14+3´5+10´22=444.
Отметим, что число заполненных (базисных) клеток равно т + п - 1= 7, то есть, действительно построен опорный план перевозок.
При построении опорного плана перевозок в рассмотренной задаче на каждом шаге, кроме последнего, либо исчерпывался запас базы (но оставалась невыполненной заявка), либо выполнялась заявка магазина (но оставалась неиспользованной часть запаса базы). Может оказаться, что на некотором (не последнем!) шаге будет одновременно выполнена заявка магазина и исчерпан запас базы, тогда число заполненных клеток окажется меньше, чем т + п - 1. В этом случае следует записать нулевую перевозку в ту клетку, которая заполнялась бы, если бы остаток запаса данной базы не был бы равен нулю. Эта клетка в дальнейшем считается базисной.
Проверка оптимальности транспортного плана методом потенциалов
|
|
|
При решении транспортной задачи, как и при решении любой задачи линейного программирования, осуществляется последовательный переход от одного опорного плана к другому. При этом на каждом шаге осуществляется замена одной базисной переменной на одну свободную, то есть, в транспортной таблице одна свободная клетка становится базисной, а одна базисная - свободной.
Рассмотрим опорный план, построенный в таблице 2. Предположим, что мы хотим сделать свободную клетку (A4, B2) базисной клеткой или запланировать перевозку с четвертой базы во второй магазин. С этой целью запишем в клетку положительное значение, равное а единиц:
Таблица 12
| Базы | Магазины | Запас | |||||||
| B1 | B2 | B3 | A4 | ||||||
| A1 | 7 | 3 | 4 | 2 | 15 | ||||
| 15 | |||||||||
| A2 | 6 | 1 | 4 | 6 | 31 | ||||
| 17-a | 14+a | ||||||||
| A3 | 6 | 9 | 5 | 3 | 25 | ||||
| 6+a | 14-a | 5 | |||||||
| A4 | 10 | 4 | 7 | 9 | 22 | ||||
| 22-a | +a | ||||||||
| Спрос | 28 | 17 | 28 | 20 | |||||
Тогда, чтобы сумма объемов перевозок в каждой строке оставалась равной ее запасу, а в столбце - заявке, нужно:
уменьшить на а единиц объем перевозки в клетке (A4, B1),
увеличить на а единиц объем перевозки в клетке (A3, B1),
уменьшить на а единиц объем перевозки в клетке (A3, B3),
увеличить на а единиц объем перевозки в клетке (A2, B3),
уменьшить на а единиц объем перевозки в клетке (A2, B2).
Таким образом, осуществляется «переброска» а единиц товара по замкнутому контуру, изображенному пунктиром в таблице 3. Такой контур называется циклом.
Цикл - это замкнутая ломаная, соединяющая несколько клеток таблицы и совершающая в каждой из них поворот на 90°. Две последовательные вершины цикла лежат либо в одной строке, либо в одном столбце. В одной из них объем перевозки увеличивается (в клетке ставится знак +), в другой - уменьшается на столько же единиц (в клетке ставится знак -). Примеры циклов различных конфигураций показаны на рис. 1:
| - | + | - | + | - | + | ||||||
| + | |||||||||||
| - | + | - | |||||||||
| + | - | - | + | + | - |
Рис. 4 - Примеры циклов
|
|
|
Так как при переходе от одного опорного плана к другому мы осуществляем замену одной свободной клетки на одну базисную, то переброска должна осуществляться по циклу, содержащему только одну свободную клетку. Такой цикл называется циклом пересчета для данной свободной клетки.
Можно доказать, что для любой свободной клетки в опорном плане перевозок существует единственный цикл пересчета. Для того, чтобы одна из базисных клеток после переброски стала свободной, значение перевозки в этой клетке должно стать равным нулю. Ясно, что это может быть только клетка, в которой стоит знак (-). Поэтому количество товара, перебрасываемого по циклу пересчета, должно быть равно наименьшей из величин перевозок, стоящих в отрицательных вершинах цикла. Например, если в таблице 3 положить а=min(22, 14, 17)=14, то, перебросив 14 единиц товара по указанному циклу пересчета, приходим к новому опорному плану:
Таблица 13
| Базы | Магазины | Запас | ||||||||
| B1 | B2 | B3 | A4 | |||||||
| A1 | 7 | 3 |
| 4 | 2 | 15 | ||||
|
| 15 | |||||||||
| A2 | 6 | 1 |
| 4 | 6 | 31 | ||||
| 3 | 28 | |||||||||
| A3 | 6 | 9 |
| 5 | 3 | 25 | ||||
| 20 |
| 5 | ||||||||
| A4 | 10 | 4 | 7 | 9 | 22 | |||||
| 8 | 14 |
| ||||||||
| Спрос | 28 | 17 | 28 | 20 | ||||||
Осталось уяснить, в каком случае переброска по циклу позволяет уменьшить суммарную стоимость всех перевозок.
Назовем ценой цикла, начинающегося в клетке (Ai, Bk), величину gik, равную приращению суммарной стоимости перевозок в результате переброски по циклу одной единицы товара. Цена цикла равна сумме стоимостей, стоящих в вершинах цикла, причем стоимость берется со знаком плюс, если перевозка от базы к магазину увеличивается (в клетке стоит знак +), и минус - в противном случае.
Например, цена цикла, изображенного пунктирной линией в таблице 3, равна:
g42 = 4 - 10 + 6 - 5 + 4 - 1 = - 2.
|
|
|
При переброске по циклу, начинающемуся в клетке (Ai, Bk), а единиц товара приращение суммарной стоимости перевозок равно
DE=a´gik.
Очевидно, что улучшение плана происходит только в случае, если DE < 0, а это равносильно тому, что gik < 0.
При переходе к плану, приведенному в таблице 4, приращение суммарной стоимости перевозок равно
DE= 14´(-2) = -28,
то есть, значение целевой функции уменьшается на 28 единиц. Поскольку для первого плана суммарная стоимость перевозок равнялась E = 444, для нового плана будем иметь:
¢= E+a´g42 = 444 - 28 = 416.
Итак, последовательность решения транспортной задачи такова. Строится опорный план перевозок. Если для любой свободной клетки в этом плане цена цикла пересчета неотрицательна, то план оптимален. Если же имеется свободная клетка с отрицательной ценой цикла пересчета, то план можно улучшить, перебросив некоторое количество товара по циклу пересчета, соответствующему этой клетке.
Существует метод, который позволяет находить свободные клетки с отрицательной ценой цикла. Этот метод называется методом потенциалов. Он состоит в следующем.
Предположим, что мы построили опорный план перевозок. Сопоставим каждой базе Ai число ai и каждому магазину Bk число bk так, чтобы для любой базисной клетки плана выполнялось условие
| ai +bk = cik. | (1) |
Числа ai и bk называются потенциалами баз (строк) и магазинов (столбцов). Так как в опорном плане имеется т + п - 1 базисных клеток, то для нахождения потенциалов нужно решить систему из т + п - 1 уравнений с т + п неизвестными. Поскольку число неизвестных на 1 больше числа уравнений, значение одного потенциала можно выбрать произвольно (например, положить его равным нулю).
Рассмотрим опорный план, полученный в таблице 4. Составим систему уравнений для вычисления потенциалов, соответствующих этому плану:
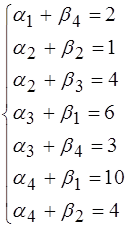 (2) (2)
|
Выбирая, например, a1=0, из (2) последовательно получаем:
b4=2, a3=1, b1=5, a4=5, b2=-1, a2=2, b3=2.
Обычно потенциалы записываются в дополнительных строке и столбце таблицы, в которой записан опорный план. Перепишем таблицу 4, заменив в ней столбец обозначений баз столбцом для потенциалов ai и строку обозначений магазинов строкой для потенциалов bk:
Таблица 14
| Потенциалы баз | Потенциалы магазинов | Запас | ||||||||||
| b1=5 | b2=-1 | b3=2 | b4=2 | |||||||||
| a1=0 | 7 | 3 |
| 4 | 2 | 15 | ||||||
|
| 15 | |||||||||||
| a2=2 | 6 | 1 |
| 4 | 6 | 31 | ||||||
| 3 | 28 | |||||||||||
| a3=1 | 6 | 9 |
| 5 | 3 | 25 | ||||||
| 20 |
| 5 | ||||||||||
| a4=5 | 10 | 4 | 7 | 9 | 22 | |||||||
| 8 | 14 |
| ||||||||||
| Спрос | 28 | 17 | 28 | 20 | ||||||||
На практике, как правило, система (2) для определения потенциалов строк и столбцов не выписывается. Для их нахождения поступают следующим образом:
в таблице, содержащей опорный план, ищут строку (столбец) с наибольшим количеством базисных клеток, ее (его) потенциал полагают равным нулю, используя соотношение (1) и стоимости базисных клеток, последовательно (визуально) определяют остальные потенциалы.
Рассмотрим алгоритм использования найденных потенциалов для проверки оптимальности опорного плана.
Назовем псевдостоимостью cik* клетки (Ai, Bk) сумму потенциалов, соответствующих этой клетке
* = ai +bk.
Очевидно, что для базисных клеток cik*=cik. Можно доказать, что для любой свободной клетки (Ai, Bk) в опорном плане перевозок справедливо равенство
gik = cik - cik*,
где gik - цена цикла пересчета для клетки (Ai, Bk). Отсюда следует, что если хотя бы в одной свободной клетке псевдостоимость превышает стоимость, то цена цикла пересчета для этой клетки отрицательна, и план можно улучшить.
Критерий оптимальности транспортного плана
План оптимален, если во всех клетках таблицы псевдостоимости не превышают стоимостей.
Проверим оптимальность рассматриваемого опорного плана. Рассчитаем псевдостоимости свободных клеток и запишем их в левом верхнем углу свободных клеток таблицы 15:
Таблица 15
| Потенциалы баз | Потенциалы магазинов | Запас | ||||||||
| b1=5 | b2=-1 | b3=2 | b4=2 | |||||||
| a1=0 | 5 | 7 | -1 | 3 | 2 | 4 | 2 | 15 | ||
|
| 15 | |||||||||
| a2=2 | 7 | 6 | 1 |
| 4 | 4 | 6 | 31 | ||
| 3 | 28 | |||||||||
| a3=1 | 6 | 0 | 9 | 3 | 5 | 3 | 25 | |||
| 20 |
| 5 | ||||||||
| a4=5 | 10 | 4 | 7 | 7 | 7 | 9 | 22 | |||
| 8 | 14 |
| ||||||||
| Спрос | 28 | 17 | 28 | 20 | ||||||
Проверим условие оптимальности плана, сравнивая псевдостоимости и стоимости свободных клеток (для базисных клеток они по построению совпадают). Поскольку в клетке (A2, B1) псевдостоимость превышает стоимость, план, записанный в таблице 6, не оптимален.
Построим цикл пересчета для этой клетки:
Таблица 16
| Базы | Магазины | Запас | ||||||||
| B1 | B2 | B3 | A4 | |||||||
| A1 | 7 | 3 |
| 4 | 2 | 15 | ||||
|
| 15 | |||||||||
| A2 | 6 | 1 |
| 4 | 6 | 31 | ||||
| +a | 3-a | 28 | ||||||||
| A3 | 6 | 9 |
| 5 | 3 | 25 | ||||
| 20 |
| 5 | ||||||||
| A4 | 10 | 4 | 7 | 9 | 22 | |||||
| 8-a | 14+a |
| ||||||||
| Спрос | 28 | 17 | 28 | 20 | ||||||
Используя данные таблицы 6, найдем цену цикла:
g21 = c21 - c21* = 6 - 7 = - 1.
Определим величину перевозки по новому маршруту: а=min(8, 3)=3.
Таким образом, клетка (A2, B1) становится базисной, а клетка (A2, В2) - свободной. Выпишем новый план перевозок:
Таблица 17
| Базы | Магазины | Запас | |||||||
| B1 | B2 | B3 | A4 | ||||||
| A1 | 7 | 3 | 4 | 2 | 15 | ||||
| 15 | |||||||||
| A2 | 6 | 1 | 4 | 6 | 31 | ||||
| 3 | 28 | ||||||||
| A3 | 6 | 9 | 5 | 3 | 25 | ||||
| 20 | 5 | ||||||||
| A4 | 10 | 4 | 7 | 9 | 22 | ||||
| 5 | 17 | ||||||||
| Спрос | 28 | 17 | 28 | 20 | |||||
Вычислим стоимость полученного плана:
¢¢= E¢+a´g21 = 416 - 3 = 413.
Проверим оптимальность нового опорного плана. Поскольку наибольшее число базисных клеток (три) в первом столбце таблицы, положим его потенциал равным нулю, последовательно (визуально) определим потенциалы остальных строк и столбцов, найдем псевдостоимости свободных клеток:
Таблица 18
| Потенциалы баз | Потенциалы магазинов | Запас | ||||||||
| b1=0 | b2=-6 | b3=-2 | b4=-3 | |||||||
| a1=5 | 5 | 7 | -1 | 3 | 3 | 4 | 2 | 15 | ||
|
| 15 | |||||||||
| a2=6 | 6 | 0 | 1 |
| 4 | 3 | 6 | 31 | ||
| 3 | 28 | |||||||||
| a3=6 | 6 | 0 | 9 | 4 | 5 | 3 | 25 | |||
| 20 |
| 5 | ||||||||
| a4=10 | 10 | 4 | 8 | 7 | 7 | 9 | 22 | |||
| 5 | 17 |
| ||||||||
| Спрос | 28 | 17 | 28 | 20 | ||||||
Поскольку в клетке (A4, B3) псевдостоимость превышает стоимость, транспортный план не оптимален. Построим цикл пересчета для этой клетки:
Таблица 19
| Базы | Магазины | Запас | |||||||
| B1 | B2 | B3 | A4 | ||||||
| A1 | 7 | 3 | 4 | 2 | 15 | ||||
| 15 | |||||||||
| A2 | 6 | 1 | 4 | 6 | 31 | ||||
| 3+a | 28-a | ||||||||
| A3 | 6 | 9 | 5 | 3 | 25 | ||||
| 20 | 5 | ||||||||
| A4 | 10 | 4 | 7 | 9 | 22 | ||||
| 5-a | 17 | +a | |||||||
| Спрос | 28 | 17 | 28 | 20 | |||||
Используя данные таблицы 9, найдем цену цикла:
g43 = c43 - c43* = 7 - 8 = - 1.
Определим величину перевозки по новому маршруту:
а=min(28, 5)=5.
Таким образом, клетка (A4, B3) становится базисной, а клетка (A4, В1) - свободной. Выпишем новый план перевозок:
Таблица 20
| Базы | Магазины | Запас | |||||||
| B1 | B2 | B3 | A4 | ||||||
| A1 | 7 | 3 | 4 | 2 | 15 | ||||
| 15 | |||||||||
| A2 | 6 | 1 | 4 | 6 | 31 | ||||
| 8 | 23 | ||||||||
| A3 | 6 | 9 | 5 | 3 | 25 | ||||
| 20 | 5 | ||||||||
| A4 | 10 | 4 | 7 | 9 | 22 | ||||
| 17 | 5 | ||||||||
| Спрос | 28 | 17 | 28 | 20 | |||||
Вычислим стоимость полученного плана:
¢¢¢= E¢¢ + a´g43 = 413 - 5=408.
Проверим оптимальность нового опорного плана. Поскольку наибольшее число базисных клеток (две), например, в первом столбце таблицы, положим его потенциал равным нулю, последовательно определим потенциалы остальных строк и столбцов, найдем псевдостоимости клеток:
Таблица 21
| Потенциалы баз | Потенциалы магазинов | Запас | ||||||||
| b1=0 | b2=-5 | b3=-2 | b4=-3 | |||||||
| a1=5 | 5 | 7 | 0 | 3 | 3 | 4 | 2 | 15 | ||
|
| 15 | |||||||||
| a2=6 | 6 | 1 | 1 |
| 4 | 3 | 6 | 31 | ||
| 8 | 23 | |||||||||
| a3=6 | 6 | 1 | 9 | 4 | 5 | 3 | 25 | |||
| 20 |
| 5 | ||||||||
| a4=9 | 9 | 10 | 4 | 7 | 6 | 9 | 22 | |||
| 17 | 5 |
| ||||||||
| Спрос | 28 | 17 | 28 | 20 | ||||||
Поскольку во всех свободных клетках псевдостоимость не превышают стоимости, рассматриваемый план

является оптимальным. Стоимость плана x (минимальные транспортные издержки) равна 408.
|
|
|


