Главная | Обратная связь | Поможем написать вашу работу!

Внутренние силы и напряжения

Моменты инерции сечения

Рис. 3.3

В дополнение к статическим моментам в системе координат x0y (рис. 3.1)рассмотрим три интегральных выражения:

(3.7)

Первые два интегральных выражения называются осевыми моментами инерции относительно осей x и y, а третье - центробежным моментом инерции сечения относительно осей x, y. Для сечений, состоящих из n-числа областей (рис. 3.3), формулы (3.7) по аналогии с (3.6) будут иметь вид:

Рассмотрим, как изменяются моменты инерции сечения при параллельном переносе координатных осей x и y (см. рис. 3.2). Преобразуя формулы (3.7) с учетом выражения (3.2), получим:

(3.8)

Если предположить, что оси x1 и y1 (см. рис. 3.2) являются центральными, тогда и выражения (3.8) упрощаются и принимают вид:

(3.9)

Рис. 3.4

Определим осевые моменты инерции прямоугольника относительно осей x и y, проходящих через его центр тяжести (рис. 3.4). В качестве элементарной площадки dF возьмем полоску шириной b и высотой dy (рис. 3.4). Тогда будем иметь:

Аналогичным образом можно установить, что:

Для систем, рассматриваемых в полярной системе координат (рис. 3.5, а), вводится также полярный момент инерции:

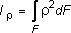
где r - радиус-вектор точки тела в заданной полярной системе координат.

Рис. 3.5

Вычислим полярный момент инерции круга радиуса R. На рис. 3.5, a показана элементарная площадка, очерченная двумя радиусами и двумя концентрическими поверхностями, площадью

dF = r dr dj.

Интегрирование по площади заменим двойным интегрированием:

.Hайдем зависимость между полярным и осевыми моментами инерции для круга. Из геометрии видно (рис. 3.5, б), что

r2 = x2 + y2,

следовательно,

Так как оси x и y для круга равнозначны, то Ix = Iy = .

Полярный момент инерции кольца может быть найден как разность моментов инерции двух кругов: наружного (радиусом R) и внутреннего (радиусом r):

9) Главные оси и главные моменты инерции Рассмотрим, как изменяются моменты инерции плоского сечения при повороте осей координат из положения x и y к положению u и v. Из рис. 3.5, б легко установить, что

u = y sin a + x cos a; v = y cos a - x sin a. (3.10) Из выражений:

с учетом (3.10) после несложных преобразований получим:

(3.11)

Складывая первые два уравнения, получим:

Iu + Iv = Ix + Iy = Ir, (3.12)

Где ; Ir - полярный момент инерции сечения, величина которого, как видно, не зависит от угла поворота координатных осей.

Дифференцируя в (3.11) выражение Iu по a и приравнивая его нулю, находим значение a = a0, при котором функция Iu принимает экстремальное значение:

(3.13)

С учетом (3.12) можно утверждать, что при a = a0 один из осевых моментов Iu или Iv будет наибольшим, а другой наименьшим. Одновременно при a = a0 Iuv обращается в нуль, что легко установить из третьей формулы (3.11).

Декартовы оси координат, относительно которых осевые моменты инерции принимают экстремальные значения, называются главными осями инерции. Осевые моменты инерции относительно главных осей называются главными и определяются из (3.11) с учетом (3.13) и имеют вид:. (3.14)

Момент сопротивления относительно некоторой оси – величина равная мо-менту инерции относительно той же оси отнесенному к расстоянию (y_max или z_max) до наиболее удаленной от этой оси точкиW y= Iy/zmax; Wz=Iz/ymax. Размерность моментов сопротивления метры кубические в СИ Радиусом инерции сечения относительно некоторой оси, называется величи-на, определяемая из соотношения:

iz=√Iz/ Fiy=√Iy/F Радиус инерции выражается в м в системе СИ

10)Осевые моменты сопротивления для простейших сечений (Ixc и Iyc - центральные моменты инерции сечений):

1. Для прямоугольника (рис. 4.10).

2. Для треугольника (рис.4.11).

(для верхних волокон).

Аналогично можно вычислить моменты сопротивления относительно оси у левых и правых волокон Wул,Wуп

3. Для круга (рис. 4.12).

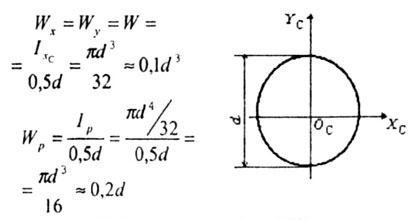
4. Для полукруга (рис.4.13).

5. Для трубчатого сечения (рис. 4.14).

Полярный момент сопротивления для трубчатого сечения.

Внутренние силы и напряжения

Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только нормальные силы, а прочие силовые факторы равны нулю.Рассмотрим однородный прямолинейный стержень длиной l и площадью поперечного сечения F, на двух концах которого приложены две равные по величине и противоположно направленные центральные продольные силы Р (рис. 2.1, а). Поместим начало плоской системы координат yz в центре тяжести левого сечения, а ось z направим вдоль продольной оси стержня. Для определения величин внутренних усилий воспользуемся методом сечений. Задавая некоторое сечение на расстояние z (0 £ z £ l) от начала системы координат и рассматривая равновесие левой относительно заданного сечения части стержня (рис. 2.1, б), приходим к следующему уравнению: P + Nz = 0,откуда следует, что Nz = P = const. Примем для Nz следующее правило знаков. Если Nz направлена от сечения, т.е. вызывает положительную деформацию (растяжение), то она считается положительной. В обратном случае - отрицательной.

Рис. 2.1

Нормальная сила Nz приложена в центре тяжести сечения, является равнодействующей внутренних сил в сечении и, в соответствии с этим, определяется следующим образом:

Но из этой формулы нельзя найти закон распределения нормальных s напряжений в поперечных сечениях стержня. Для этого обратимся к анализу характера его деформирования.

Если на боковую поверхность этого стержня нанести прямоугольную сетку (рис. 2.1, б), то после нагружения поперечные линии а-а, b-b и т.д. переместятся параллельно самим себе, откуда следует, что все поверхностные продольные волокна удлинятся одинаково. Если предположить также, что и внутренние волокна работают таким же образом, то можно сделать вывод о том, что поперечные сечения в центрально растянутом стержне смещаются параллельно начальным положениям, что соответствует гипотезе плоских сечений, введенной швейцарским ученым Д. Бернулли, гласящей, что плоские сечения до деформации остаются плоскими и после деформации. Значит, все продольные волокна стержня находятся в одинаковых условиях, а следовательно, нормальные напряжения во всех точках поперечного сечения должны быть также одинаковы и равны , где F - площадь поперечного сечения стержня.Высказанное предположение о равномерном распределении внутренних сил в поперечном сечении справедливо для участков, достаточно удаленных от мест: резкого изменения площади поперечного сечения (рис. 2.1, в); скачкообразного изменения внешних нагрузок; скачкообразного изменения физико-механических характеристик конструкций. Основанием для такого утверждения служит принцип Сен-Венана, справедливый для любого типа напряженного состояния и формулируемый следующим образом: особенности приложения внешних нагрузок проявляются, как правило, на расстояниях, не превышающих характерных размеров поперечного сечения стержня. Эпюрами продольных сил и нормальных напряжений называют графики, показывающие законы изменения сил и напряжений в поперечных сечениях по длине стержня.

12)СЕН-ВЕНАНА ПРИНЦИП - в теории упругости - положение, согласно которому уравновешенная система сил, приложенных к какой-либо части твердого тела, вызывает в нем напряжения, быстро убывающие по мере удаления от этой части, и может быть заменена эквивалентной системой сил. Сформулирован А. Сен-Венаном в 1855. Концентрация напряжений Вблизи различного рода отверстий, надрезов, выточек и, вообще,(мест резкого изменения поперечных размеров распределение напряжений становится существенно неравномерным, и возникают зоны повышенных напряжений. Например, при одноосном равномерном растяжении напряжениями σ тонкой пластинки шириной Н с небольшим (d<Н/5) круглым отверстием распределение напряжений по поперечному сечению, проходящему через центр отверстия, оказывается существенно неравномерным с пиками напряжений в точках А и В контура отверстия (4.21). Точное решение показывает, что нормальные напряжения в радиальных сечениях на контуре отверстия изменяются по закону σθ=σ(1-2cos2θ) и в точках А и В при θ=π/2 достигают величины σmax=3σ, а при θ=0, т. е. в сечении, параллельном линии действия нагрузки, действуют сжимающие напряжения σθ=σ, равные по величине приложенным к пластинке напряжениям.

Рис. 4.21. Концентрация напряжений в пластине с отверстием Неравномерность распределения напряжений по поперечному сечению имеет место и при центральном растяжении ступенчатого бруса (4.22), причем максимальные напряжения быстро увеличиваются по мере уменьшения радиуса закругления переходной части (галтели). Большие местные напряжения возникают также в зоне контакта деталей (контактные напряжения).

Явление возникновения значительных местных напряжений называется концентрацией напряжений, а причина, вызвавшая концентрацию - концентратором напряжений. Концентрация напряжений характеризуется коэффициентом концентрации α. Величину α также называют теоретическим коэффициентом концентрации. Коэффициентом концентрации α называется отношение действительного напряжения σmax в наиболее напряженной точке к номинальному напряжению σn в той же точке, т. е. или . Номинальными называются напряжения, вычисленные по формулам сопротивления материалов, не учитывающим явление концентрации напряжений. В тех случаях, когда возникают трудности в вычислении номинальных напряжений в сечении с концентратором напряжений, за номинальные принимают напряжения в неослабленном сечении детали. В настоящее время методами теории упругости и экспериментальными методами (обычно путем испытания образцов из оптически активного материала в поляризованном свете) определены величины коэффициентов концентрации для многих практически важных случаев. Расчетные формулы, таблицы и графики для определения коэффициентов концентрации приводятся в справочной литературе. На Рис. 4.22 представлен характер зависимости коэффициента концентрации от отношения радиуса галтели ρ к диаметру d в случае осевого растяжения ступенчатого бруса.

Рис. 4.22. Концентрация напряжений для галтельного соединения Концентраторы напряжений – местные резкие изменения однородности (формы и, следовательно, жесткости) конструкции, приводящие к резкому местному (локальному) повышению напряжений в конструкции. На рисунке показано действие растягивающей внешней нагрузки, равномерно распределенной по краям простейших конструктивных элементов – листов. Пунктирные линии представляют собой так называемые траектории напряжений, вдоль которых напряжение передается от молекулы к молекуле. Для гладкого листа эти линии параллельны, напряжения в любом сечении листа одинаковы.

Силы, передающиеся по траекториям напряжений в листах с концентраторами (надрез в кромке листа, отверстие в центре листа), обходят разрыв в материале. Плотность траекторий напряжений увеличивается, и локальные напряжения у края концентратора возрастают (иногда многократно). В этих местах может произойти нарушение (разрыв) межатомных связей, возникнут микротрещины, распространение которых ведет к разрушению конструкции.

13)Удлинение стержня и закон Гука Рассмотрим однородный стержень с одним концом, жестко заделанным, и другим - свободным, к которому приложена центральная продольная сила Р (рис. 2.2). До нагружения стержня его длина равнялась l -после нагружения она стала равной l + Dl (рис. 2.2). Величину Dl называют абсолютным удлинением стержня.

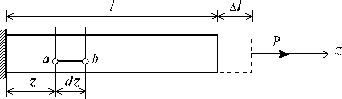Рис. 2.2 Если в нагруженном стержне напряженное состояние является однородным, т.е. все участки стержня находятся в одинаковых условиях, деформация e остается одной и той же по длине стержня и равной (2.1)

Если же по длине стержня возникает неоднородное напряженное состояние, то для определения его абсолютного удлинения необходимо рассмотреть бесконечно малый элемент длиной dz (рис. 2.2). При растяжении он увеличит свою длину на величину D dz и его деформация составит: (2.2) В пределах малых деформаций при простом растяжении или сжатии закон Гука записывается в следующем виде:s = E e. (2.3) Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости материала первого рода. Из совместного рассмотрения уравнений (2.2) и (2.3) получим: ,откуда с учетом того, что и ,окончательно получим: Если стержень изготовлен из однородного изотропного материала с Е = const, имеет постоянное поперечное сечение F = const и нагружен по концам силой Р, то из (2.4) получим (2.5) При решении многих практических задач возникает необходимость, наряду с удлинениями, обусловленными действием механических нагрузок, учитывать также удлинения, вызванные температурным воздействием. В этом случае пользуются принципом независимости действия сил, и полные деформации рассматривают как сумму силовой и температурной деформаций: , где a - коэффициент температурного расширения материала; t -перепад температуры тела. Для однородного стержня, нагруженного по концам продольными силами Р и равномерно нагретого по длине, получим:. (2.7)

Коэффициент Пуассона характеризует упругие свойства материала. При приложении к телу растягивающего усилия оно начинает удлиняться (то есть длина увеличивается), а поперечное сечение уменьшается. Коэффициент Пуассона показывает, во сколько раз изменяется поперечное сечение деформируемого тела при его растяжении или сжатии. Для абсолютно хрупкого материала коэффициент Пуассона равен 0, для абсолютно упругого — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он примерно равен 0,5. (Измеряется в относительных единицах (мм/мм, м/м))

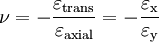где ν — коэффициент Пуассона.

— деформация в поперечном направлении (отрицательный для осевого растяжения, положительный для осевого сжатия)

— продольная деформация (положительный для осевого растяжения, отрицательный для осевого сжатия).

14)Жёсткость — способность конструктивных элементов деформироваться при внешнем воздействии без существенного изменения геометрических размеров. В случаях малых одномерных деформаций (в пределах зоны упругости, где справедлив Закон Гука) жёсткость можно определить как произведение модуля упругости Е (при растяжении, сжатии и изгибе) или G (при сдвиге и кручении) на соответствующую геометрическую характеристику сечения элемента, например, площадь поперечного сечения или осевой момент инерции. Понятие жёсткости широко используется при решении задач сопротивления материалов. Потенциальная энергия деформации Внешние силы, приложенные к упругому телу и вызывающие изменение геометрии тела, совершают работу А на соответствующих перемещениях. Одновременно с этим в упругом теле накапливается потенциальная энергия его деформирования U. При действии динамических внешних нагрузок часть работы внешних сил превращается в кинетическую энергию движения частиц тела К. Приняв энергетическое состояние системы до момента действия данных сил равным нулю, и в условиях отсутствия рассеивания энергии, уравнение баланса энергии можно записать в следующем виде:А = U + K.При действии статических нагрузок К = 0, следовательно,А = U.Это означает, что при статическом нагружении работа внешних сил полностью преобразуется в потенциальную энергию деформации. При разгрузке тела производится работа за счет потенциальной энергии деформации, накопленной телом. Таким образом, упругое тело является аккумулятором энергии. Это свойство упругого тела широко используется в технике, например, в заводных пружинах часовых механизмов, в амортизирующих рессорах и др. В случае простого растяжения (сжатия) для вывода необходимых расчетных зависимостей потенциальной энергии деформации рассмотрим решение следующей задачи. На рис. 2.4, а изображен растягиваемый силой Р стержень, удлинение которого соответствует отрезку Dl, ниже показан график изменения величины удлинения стержня Dl в зависимости от силы Р (рис. 2.4, б). В соответствии с законом Гука этот график носит линейный характер.

Пусть некоторому значению силы Р соответствует удлинение стержня Dl. Дадим некоторое приращение силе DР - соответствующее приращение удлинения составит d (Dl). Тогда элементарная работа на этом приращении удлинения составит:dA = (P + d P)×d (D l) = P×d (D l) + d P × d (D l), вторым слагаемым, в силу его малости, можно пренебречь, и тогда dA = P×d (D l).

Полная работа равна сумме элементарных работ, тогда, при линейной зависимости “нагрузка - перемещение”, работа внешней силы Р на перемещении Dl будет равна площади треугольника ОСВ (рис. 2.4), т.е.А = 0,5 Р×Dl В свою очередь, когда напряжения s и деформации e распределены по объему тела V равномерно (как в рассматриваемом случае) потенциальную энергию деформирования стержня можно записать в виде: Поскольку, в данном случае имеем, что V = F l, P = s F и s = Е e, то , (2.14)

т.е. подтверждена справедливость (2.9).

С учетом (2.5) для однородного стержня с постоянным поперечным сечением и при Р = const из (2.14) получим:

. (2.15)

Билет №15 Осевая деформация прямолинейного стержня, т.е растяжение или сжатие, возникают тогда, когда все внешние нагрузки приложенные к стержню приводятся только к силам, точки приложения которых лежат на оси. При этом возникает только продольная сила F, а все остальные силовые линии равны 0. Напряженное и деформированное состояние

Различают три вида напряженного состояния:

1) линейное напряженное состояние — растяжение (сжатие) в одном направлении;

2) плоское напряженное состояние — растяжение (сжатие) по двум направлениям;

3) объемное напряженное состояние — растяжение (сжатие) по трем взаимно перпендикулярным направлениям.

Рассматривают бесконечно малый параллелепипед (кубик). На его гранях могут быть нормальные s и касательные t напряжения. При изменении положения "кубика" напряжения меняются. Можно найти такое положение, при котором нет касательных напряжений см. рис.

Площадки, по которым недействуют касательные напряжения, называются главными площадками, а нормальные напряжения на этих площадках — главными напряжениями.

Главные напряжения обозначают: s₁, s₂, s₃ и s₁> s₂> s₃

Плоское напряженное состояние

Разрежем элементарный параллелепипед (рис.а) наклонным сечением. Изображаем только одну плоскость. Рассматриваем элементарную треугольную призму (рис.б). Положение наклонной площадки определяется углом a. Если поворот от оси x против час.стр. (см. рис.б), то a>0. Нормальные напряжения имеют индекс, соответствующий оси их направления. Касательные напряжения, обычно, имеют два индекса: первый соответствует направлению нормали к площадке, второй — направлению самого напряжения (к сожалению, встречаются и другие обозначения, и другой выбор осей координат, что приводит к изменению знаков в некоторых формулах).Нормальное напряжение положительно, если оно растягивающее, касательное напряжение положительно, если оно стремится повернуть рассматриваемую часть элемента относительно внутренней точки по час.стр (для касательного напряжения в некоторых учебниках и вузах принято обратное). Напряжения на наклонной площадке:

или Закон парности касательных напряжений: если по площадке действует касательное напряжение, то по перпендикулярной к ней площадке будет действовать касательное напряжение, равное по величине и противоположное по знаку. (t_xz= — t_zx)

Задачи, в которых все реакции связей определяются из условий равновесия, называются статически определимыми. Если число неизвестных реакций связей превышает число уравнений равновесия, задача становится статически неопределимой. Степенью статической неопределимости называется разность между числом искомых неизвестных усилий и числом независимых уравнений равновесия, которые для данной системы можно составить. Для решения статически неопределимых задач к уравнениям равновесия добавляют условия совместности деформаций, являющиеся уравнениями, связывающими между собой деформации или перемещения отдельных частей тела. В алгоритме решения данных задач присутствуют три стороны решения:1) Статическая сторона задачи:Для определения неизвестных опорных реакций записываем уравнения статики, т.е проецируем все имеющиеся силы и реакции на оси координат а также записываем уравнение моментов для данной системы если это возможно. Т.к в статически неопределимых задачах неизвестных больше чем уравнений статики, то нам нужно составить столько уравнений сколько и неизвестных реакций нужно найти. Для этого используется 2) Геометрическая сторона задачи (условия совместности деформаций). Нужно рассматривать схему деформирования системы(а именно систему до и после деформации одновременно).Затем либо с помощью подобие треугольников, либо с помощью любого другого геометрического выражения должны составить уравнения изменения длины участка системы до и после деформации.Например:L2=L1*cos@

Имея столько уравнении сколько и неизвестных наступает следующий момент:3) Физическая сторона задачи. С помощью физических формул таких как Закон Гука определяем изменения длины L1 и L2. с учетом уравнения совместности деформаций L2=L1*cos@, приравниваем значения удлинений. Решая совместно уравнения равновесия и уравнение совместности деформаций, находим усилия в стержнях. Что и является искомым в статически неопределимых задачах.

Билет №16 Механические характеристики и свойства материалов Для решения практических задач по применению тех или иных материалов необходимо иметь числовые характеристики их прочностных свойств. Например при изучении процессов штамповки и гибки нужны числовые показатели, характеризующие способность материала к пластической деформации. Достаточно часто необходимо иметь данные о способности материала противостоять высоким и низким температурам. В связи с этим создано много испытаний. Классификация испытаний:1) По виду нагружения делятся: а) на статические б)на динамические в) испытания на выносливость2) По характеру воздействия делятся на: a)кратковременные б)длительные3) По виду деформации делятся на: а)на растяжение б) на сжатие в)на сдвиг г) на кручение д) на изгиб е) в условиях сложного напряжённого состояния4 )По температурному режиму: а)при нормальных условиях Т=20 С б)при высоких Т в)при низких Т5) По наличию агрессивной среды: а)в нейтральной среде б) в агрессивной среде

6) Специальные испытанияСреди эксперементальных методов широко используются:Метод тензометрии( является основным в экспериментальном определении напряжений при испытаниях, заключается в измерении при помощи специальных точных приборов, называемых тензометрами, деформаций в какой-либо точке (зоне) элемента конструкции и нахождении по величине этих деформаций, используя зависимость Гука, величин напряжений.) Метод лаковых покрытий (для выявления общего распределения деформаций и напряжений и определения наиболее нагруженных зон деталей)

1) Рентгеновский метод (позволяет определить упругие деформации металлов с кристаллической решёткой) Метод полос Муара (используется при исследовании напряжённого состояния на деталях плавной формы)

2) Поляризационно-оптический (основан на интерференции света, прошедшего модель из прозрачного, оптически чувствительного материала)

Некоторые материалы в разных условиях деформирования ведут себя по-разному. Поэтому говорят о состоянии материала в условиях протекание деформации: пластичное либо хрупкое состояние. Факторы влияющие на то или иное состояние:

1) Скорость деформирования 2) Температура 3) Степень неоднородности поля напряжения в теле. Чем эти параметры выше и чем ниже температура, тем более вероятно хрупкость материала Изучение свойств материала производится на изготовленных из него образцах, стандартной формы. Нагружение образца осуществляется с помощью специальных машин. Материалы в процессе деформирования под нагрузкой вплоть до разрушения ведут себе по-разному: 1) Одни(пластичное поведение) в момент разрушения образца претерпевают значительные деформации, неизменяющиеся после снятия нагрузки 2) Другие (хрупкие) разрушение образца наступает без видимых изменений в образце Пластические материалы: алюминий, медь свинец.

12 3 Следующая ⇒

Воспользуйтесь поиском по сайту: