Билет №21 Потенциальная энергия деформации и работа внешних сил, приложенных к упругому телу.

Внешние силы в процессе деформации тела производят работу. Часть затраченной на деформацию энергии поглощается телом и накапливается в нем в виде потенциальной энергии, называемой потенциальной энергией деформации. Остальная часть расходуется на необратимые процессы - нагрев тела, изменение его электромагнитных свойств и т. д. Соотношение между этими двумя слагаемыми энергии внешних сил изменяется в процессе нагружения тела. В пределах упругих деформаций затрата энергии на необратимые процессы весьма незначительна, и поэтому можно считать, что в пределах упругости работа внешних сил полностью переходит в потенциальную энергию деформации. Таким образом, упругое тело является как бы аккумулятором энергии. За пределами упругости большая часть работы внешних сил затрачивается на необратимые процессы, а при разгрузке выделяется лишь часть энергии, связанная с упругими деформациями тела. При разгрузке идеально упругого тела накопленная в нем потенциальная энергия полностью расходуется на восстановление его первоначальной формы и размеров, причем эту работу производят внутренние силы. Следовательно, потенциальная энергия деформации равна работе внутренних сил упругости на перемещениях точек их приложения, и поэтому всегда может быть выражена через эти силы. Приняв энергетическое состояние системы в условиях отсутствия энергии W=U+K; При действии статических нагрузок кинетическая энергия равна нулю. Это означает, что при статическом нагружении работа внешних сил полностью преобразуется в потенциальную энергию деформации. В случае простого растяжения или сжатия для вывода энергии рассмотрим задачу (ниже рис.) В Соответствии с Законом Гука величина линейной деформации и силы F носит линейный характер. Дадим силе F небольшое приращение F+Df, которое соответствует приращению удлинения, dW=(F+dF)*d(^L)= Fd(^L)+dF*d(^L)= Fd(^L), (т.к. dF*d(^L)-можно пренебречь ввиду малости). Полная работа равна сумме элементарных робот.

Билет № 22. Влияние фактора времени и температуры на механические характеристики материалов. Ползучесть. Релаксация. Последействие. Обобщающий анализ свойств материала с учетом температуры и времени оказывается очень сложным и не укладывается и простые экспериментально полученные кривые, подобные диаграммам растяжения. Функциональная зависимость между четырьмя параметрами s, e, температурой t° и временем t: f(s,e, t°, t)=0 не является однозначной и содержит в сложном виде дифференциальные и интегральные соотношения входящих в нее величин. Так как в общем виде аналитическое или графическое описание указанной функции дать не удается, то влияние температуры и фактора времени рассматривается в настоящее время применительно к частным классам задач. Деление на классы производится и основном по типу действующих внешних сил. Различают медленно изменяющиеся, быстро и весьма быстро изменяющиеся нагрузки. На рис. 13 показана зависимость от температуры модуля упругости Е, предела текучести sтр, предела прочности sвр и удлинения при разрыве e для малоуглеродистой стали в интервале 0—500°С. Как видно из приведенных кривых, модуль упругости в пределах изменения температуры до 300°С практически не меняется. Более существенные изменения претерпевают величина sвр и, особенно, d, причем имеет место, как говорят, «охрупчивание» стали — удлинение при разрыве уменьшается. При дальнейшем увеличении температуры пластичные свойства стали восстанавливаются, а прочностные показатели быстро падают. Чем выше температура, тем труднее определить механические характеристики материала. Изменение во времени деформаций и напряжений, возникающих в нагруженной детали, носит название ползучести. Частным проявлением ползучести является рост необратимых деформаций при постоянном напряжении. Это явление носит название последействия. Наглядной иллюстрацией последействия может служить наблюдаемое увеличение размеров диска и лопаток газовой турбины, находящихся под воздействием больших центробежных сил и высоких температур. Это увеличение размеров необратимо и проявляется обычно после многих часов работы двигателя. Другим частным проявлением свойств ползучести является релаксация — самопроизвольное изменение во времени напряжений при неизменной деформации. Релаксацию можно наблюдать, в частности, на примере ослабления затяжки болтовых соединений, работающих в условиях высоких температур.

 

Билет №23. Коэффициент запаса(выбор и значения для различного состояния материала). Допускаемые напряжения.1) Фактические нагрузки, действующие на деталь, и свойства материалов, из которых она изготовлена, могут значительно отличаться от тех, которые принимаются для расчета. При этом факторы, снижающие прочность детали (перегрузки, неоднородность материалов и т. д.), носят чаще всего случайный характер и предварительно не могут быть учтены. Так как детали и сооружения в целом должны безопасно работать и при этих неблагоприятных условиях, то необходимо принять определенные меры предосторожности. С этой целью напряжения, обеспечивающие безотказную работу (эксплуатации) машины или любого другого сооружения, должны быть ниже тех предельных напряжений, при которых может произойти разрушение или возникнуть пластические деформации. Таким образом, принимают(см. Формулу)

где [σ]- допускаемое напряжение; [n] - нормативный (т. е. предписываемый нормами проектирования конструкций) коэффициент запаса прочности, называемый также коэффициентом безопасности, σn - предельное напряжение материала. При статических нагрузках за предельное напряжение для хрупких материалов принимают предел прочности, для пластичных - предел текучести, так как при напряжениях, равных пределу текучести, возникают значительные пластические деформации, которые недопустимы. Таким образом, коэффициент запаса прочности вводится для того, чтобы обеспечить безопасную, надежную работу сооружения и отдельных его частей, несмотря на возможные неблагоприятные отклонения действительных условий их работы от расчетных. 2) Выбор коэффициента запаса зависит от вида нагружения, однородности и хрупкости, если известно только состояние материала, а также известен характер действия нагрузки при проектировании, то коэффициент запаса можно задавать так: 1) Если характер действия и нагрузки статический, то для пластичного материала n=2,4..2,6, а для хрупкого материала при том же характере нагрузки n=3,0..9,0. 2)При ударном характере нагрузки для пластичного материала n=2,8..5,0 3)И для переменного характера нагрузки и действия для того же пластичного материала n=5,0..15.3) Допускаемыми называют напряжения, соответствующие деформациям, допустимым при работе механизма. Допустимые деформации деталей ограничивают упругими деформациями. Так как величины допускаемых напряжений определяются величиной допустимых деформаций, при расчетах обычно используют условие прочности, которое включает в себя условие жесткости. Допускаемое напряжение связывают с механическими свойствами материала детали и определяют по формуле σ adm = σ u/ n, где σ u - предельное напряжение для материала, т.е. напряжение, при котором могут появиться заметные остаточные деформации: для пластичных материалов в качестве такового принимают условный предел текучести σ 0,2 или предел текучести σ y, а для хрупких материалов - предел прочности σ u; n - коэффициент запаса прочность.

 

 

Билет №24. Теории прочности: Критерии прочности и классические теории прочности.1) За критерий прочности принимают напряжение, деформацию, энергию деформации и т.д. Существуют различные взгляды на причины, вызывающие опасное состояние материалов. Опасное состояние наступает при достижении нормальными напряжениями значений максимальных значений. Другие считают – величины касательных напряжений. Эти критерии позволяют сравнить нормативные напряжения с опасными. Напряжённые состояния равнопрочные, если при равнопропорциональном увеличении нагрузок в несколько раз приведёт к опасному состоянию. Под эквивалентным понимают напряжение, которое следует создать в растянутом образце, чтобы его напряжённое состояние было прочным. 2) Классические теории прочности:*а) Первая теория прочности( теория наибольших нормальных напряжений): Опасное состояние материалов наступает тогда, когда наибольшее нормальное напряжение достигнет опасного значения: σэкв≤{σ}, где {σ}-опасное значение напряжения, установленное при нормальном напряжении. Эта теория прочности применима для весьма хрупких материалов.

*б) Вторая теория прочности ( теория наибольших деформаций): Нарушение прочности наступает при достижении наибольшей линейной деформации своего опасного значения, возникающей при максимальном растяжении: |ε|max≤{ε}. Применима для хрупкого состояние материала. *в) Третья теория прочности( наибольших касательных напряжений): Нарушение прочности тогда, когда наибольшее касательное напряжение достигает своего максимального значения при простом растяжении τmax≤{τ}.Т. к. При растяжении в основном возникают нормальные напряжения, то условие прочности выражаются и в эквивалентных напряжениях: σэкв≤{σ}. Эта теория подтверждается эксперементально для пластических материалов и не пригодна для хрупких материалов. *г) Четвёртая теория прочности( энергическая теория формоизменения): Опасное состояние наступает тогда, когда удельная потенциальная энергия достигает своего предельного значения uф ≤ {uф}. Энергитеческая теория прочности хорошо согласуется с пластическими материалами.

*д) Пятая теория прочности ( Теория прочности предельных состояний Морра): Согласно теории Мора, два напряженных состояния равноопасны, если для соответствующих двух главных напряжений (σ’1,σ’3 и σ’’1,σ’’3) соблюдается соотношение σ’1-k* σ’3= σ’’1-k* σ’’3. Отсюда вытекает формула для эквивалентного напряжения: экв13σэкв=σ1−k*σ3. Здесь коэффициент k представляет собой отношение предельных напряжений при одноосном растяжении и при одноосном сжатии. Теория прочности Мора позволяет установить сопротивление разрушению материалов, обладающих разными сопротивлениями растяжению и сжатию.

25. Напряженное состояние в точке. Уравнения равновесия Чтобы охарактеризовать напряженное состояние в произволь­ной точке тела, находящегося в равновесном состоянии в общем случае нагружения, выделим в ее окре­стности некоторый объем в виде элементарного параллелепипеда, грани которого перпендикулярны координатным осямПолное напряжение, возникающее на площадке параллелепи­педа может быть разложено на три составляющие, одну по нормали к площадке и две в ее плоскости.Нормальное и касательное напряжение обозначаются через  и , соответственно, с двумя индексами:  _xx ,  _yy ,...,  _zx . Первый индекс соответствует координатной оси, перпендикулярной к пло­щадке на которой действует данное напряжение, а второй  оси, вдоль которой оно направлено. Поскольку, у нормальных напряже­ний оба индекса одинаковы, то для них применяют и одномерную индексацию:  _xx =  _x ,  _yy =  _y , и  _zz =  _z . Ориентация осей является произвольной.Правило знаков примем следующее: если внешняя нормаль к площадке совпадает по направлению с положительным направле­нием соответствующей оси, то напряжение считается положитель­ным, если оно направлено вдоль положительного направления оси, вдоль которой оно действует. Так, на рис. 10.1 все напряжения положительные.Из трех условий равновесия параллелепипеда в виде суммы мо­ментов относительно координатных осей достаточно просто полу­чить важные утверждения, что  _yz =  _zy;  _zx =  _xz;  _xy =  _yx. (10.1)То есть, на двух взаимно перпендикулярных площадках состав­ляющие касательных напряжений, перпендикулярные к общему ребру, равны по величине и направлены обе либо к ребру, либо от него. Это утверждение  закон парности касательных на­пряжений, сформулированный в общем виде.Максимальное для данной точки тела касательное напряж. Возникает на площадке, параллельной вектору s2 (или  и делящей пополам прямой угол между плащадками дейстрвия s1 и s3( Определение главных напряжений и главных площадок

Если по граням выделенного элементарного параллелепипеда действуют одни только нормальные напряжения, то они называются главными напряжениями, а площадки, на которых они действуют, называются главными площадками. Можно доказать, что в каждой точке напряженного тела существуют три главные взаимно перпендикулярные площадки (рис.3.6.). Главные напряжения обозначают s1, s2, s3(или . При этом большее (с учетом знака) главное напряжение обозначается s1, а меньшее (с учетом знака) обозначается s3. Различные виды напряженного состояния классифицируются в зависимости от числа возникающих главных напряжений. Если отличны от нуля все три главных напряжения, то напряженное состояние называется трехосным или объемным (рис. 3.6). Если равно нулю одно из главных напряжений, то напряженное состояние называется двухосным или плоским. Если равны нулю два главных напряжения, то напряженное состояние называется одноосным или линейным. Для графического определения главных напряжений в элементе (рис. 3.9) необходимо выполнить следующие действия: 1)выбрать прямоугольную систему координат (σ, τ) так, чтобы ось была параллельна большему из напряжений, 2)на оси абсцисс отложить отрезки, численно равные σα и σβ; 3)в концах этих отрезков, учитывая знаки, восстановить перпендикуляры, соответственно равные τα и τβ; 4)соединить концы этих перпендикуляров и на полученном отрезке, как на диаметре, построить окружность (рис. 3.9); 5)отрезки OA и OB, отсекаемые этой окружностью на оси абсцисс будут численно равны искомым главным напряжениям; 6)s1 будет направлено по линии AM/α, а s2 будет направлено по линии AM/β.

По найденным направлениям главных напряжений, строятся главные площадки и главные напряжения. Из построения (рис. 3.9) очевидно следующее: , где

Следовательно,

Если по этим формулам получится, что αo>0,то отсчет этого угла будет против хода часовой стрелки, а при αo<0 - по ходу часовой стрелки.

26. разрушение металлов Процесс разруш. Начинается с образования трещин субмикроскопических размеров и заканчивается макроскопическим разрушением конструкции на отдельные части.В макроскопической теории прочности различ. 2 вида разруш.: 1)отрыв (в результате действ. Растягивающих напряжений), 2) срез (под действ. Касательных напряж.).Разрушение материала возможно:хрупкое—от отрыва, получающегося тогда, когда расстояние между двумя смежными элементами тела, расположенными по направ­лению силового воздействия, увеличится в результате этого воздействия настолько, что силы сцепления между этими элементами окажутся погашенными; разрушению от отрыва соответствует вторая теория прочности (теория наибольших удлинений);пластичное — от сдвига, получающегося тогда, когда будет превзойдено сопротивление взаимному сдвигу двух смежных элементов тела; разрушению от сдвига соответствует третья (теория наибольших касательных напряжений) или четвертая (энергетическая) теория прочности. Стадии развития трещины: докритическая стадия: 1) Инкубационный этап разрушения (скорость распостронения трещины возрастает), 2)период торможения(замедление роста трещины), 3) стационарный этап(скорость развития трещины постоянна), закритическая стадия: 4)ускоренный этап(рост трещины постоянно возрастает до полного разруш.) Механизмы зарождения трещин…

 

Билет №27. Основные микромеханизмы разрушения. Усталость металлов.1)Усталость металлов. Под действием циклических напряжений в металлах зарождаются и постепенно развиваются трещины, вызывающие полное разрушение детали. Разрушения могут возникать при напряжениях меньших, чем напряжения текучести и прочности. Около 80% разрушений происходит в результате циклических разрушений. Усталостная трещина зарождается в поверхностных слоях и затем развивается в глубь детали образца острый надрез. Распространение усталостных трещин обычно длительно и продолжается до тех пор, пока сечения детали не окажутся столь малыми, что действующие напряжения не превысят разрушающие. Последовательно идут следующие процессы: 1) пластическая деформация 2) зарождение трещины 3) постепенное развитие некоторых из них 4) быстрое и окончательное разрушение2) Основные микромеханизмы разрушения: 1) Транскристаллитный хрупкий скол ( характеризуется относительно гладкими фасетками разрушения с типичными картинами речного узора и характерен для условий статического напряжения) 2) Квазискол (происходит по типу транскристаллитного скола, но со значительной хрупкой деформацией) 3) Чашечный механизм разрушения (характеризуется наличием на поверхности ямок или чашек разрушения, связан с разделением образца на части) 4) Вязкий скол (происходит под действием значительных сдвиговых напряжений, как правило в изломе есть плоские и гладкие участки разрушения ) 5) Микрозёрное хрупкое разрушение (сопровождается распространением трещин вокруг зёрен, оно обусловлено наличием вдоль границ зёрен повышенной плотности частиц выделений. 6) Усталостное разрушение с образованием. (Ширина усталостной полосы соответствует скачку трещины за цикл. Строение усталостных полос зависит от режимов обработки среды и т. д. 7) Разрыв (сопровождается потерей несущей способности нагруженного тела при 100%-ой сужении площади поперечного сечения, характерен для металлов и сплавов в сверхъпластичном состоянии.

28.Критерии разрушения Изложение вопросов разрушения в курсе сопротивления материалов обычно начинается с замечания о том, что реальная прочность материалов значительно меньше теоретической, что объясняется наличием в материале различных дефектов (трещины, поры ит.п.). После этого на примере растяжения пластины бесконечной ширины с трещиной излагается энергетический критерий начала распространения трещины, предложенный механиком А. Гриффитсом (Griffith А., 1893 — 1963) в 1920 г. [376]. Силовой критерий разрушения был сформулирован позднее в 1957 г. механиком Л. Ирвином [395]. Последний также показал эквивалентность этих двух критериев. При выводе их было использовано решение задачи о напряженном состоянии пластины бесконечной ширины с трещиной. Формулы для напряжений в этой области были получены механиком X. Вестергардом (WestergaurdН.) [498] в 1939 г. Они могут быть установлены на основании решения задачи о напряженном состоянии растянутой пластины бесконечной ширины с эллиптическим отверстием, данного впервые в 1909 г. Г.В. Колосовым [189] и затем, в 1913 г., — механиком К. Инглисом (Inglis С.) [394].Д.Ирвином в 1958 г. было показано [396], что при наличии пластических деформаций в вершине трещины следует в расчетах увеличить ее длину, и приведен приближенный метод учета пластических деформаций (так называемая поправка Ирвина на пластичность).При отсутствии информации о трещинах для определения коэффициента запаса по разрушению может быть использован критерий О. Мора, аналогичный его критерию пластичности, который в рассматриваемом случае позволяет отразить различие в пределах прочности при растяжении и сжатии.А. Надаи, по-видимому, в 1950 г. [215], принял, что октаэдрическое касательное напряжение τo является функцией среднего нормального напряжения σo: τo=f(σo). Поскольку теорию О.Мора можно трактовать как теорию, устанавливающую связь касательного напряжения в некоторой площадке с нормальным напряжением в ней, теория Надаи является обобщением теории Мора. Этот вопрос обстоятельно проанализирован в работах М.М. Филоненко-Бородича [296, 298], опубликованных в 1954 и 1961 гг., и изложен в его книге [299], а также в книге [293].Заметим, что еще в 1928 г. В. Бужиньски принял [333] в несколько иной и более конкретной форме указанную выше зависимость. Именно он считал, что в предельном состоянии второй инвариант девиатора напряжений является квадратичной функцией первого инварианта тензора напряженийТри постоянных в этой зависимости определяются из трех испытаний на растяжение и сжатие образцов, и кручение тонкостенных трубок. Независимо от В.Бужиньского такое же условие предельного состояния было предложено в 1931 г. [308] Ю.И. Ягном. Существует еще ряд критериев разрушения, основанных на зависимости второго инварианта девиатора напряжений от первого инварианта тензора, часть из которых является частными случаями критерия Бужиньского — Ягна. Следует упомянуть хорошо согласующийся с результатами экспериментальных исследований критерий механиков и инженеров Георгия Степановича Писаренко (12.11.1910) и Анатолия АлексеевичаЛебедева Локальное коррозионное разрушение происходит обычно при наличии катодных и анодных микроэлементов,которые способствуют концентрации и ускорению электрохимического процесса.

При жестком облучении нейтронами или другими высокоэнергетическими частицами кристаллическая решетка металла претерпевает изменения, напоминающие те, что происходят при глубокой холодной деформации. Появляются вакансии в решетке, меж-узельные атомы, дислокации; это увеличивает скорость диффузии специфических примесей или легирующих компонентов. В процессе облучения может происходить локальное повышение температуры — так называемый «.температурный пик».В 1913 году в своей работе в журнале Transactions of the Institution of Naval Architects С. Инглис показал, что любые геометрические нерегулярности (отверстия, острые углы, трещины и т. п.), которые ранее не принимались во внимание, могут очень резко повышать локальные напряжения в узкой области. Вблизи отверстий и вершин надрезов напряжения могут превышать разрушающее напряжение материала, даже если общий уровень напряжений достаточно мал и конструкция представляется абсолютно безопасной. Почти любые отверстия, трещины и изломы очертаний твердого тела, непрерывного в других отношениях, вызывают локальное повышение напряжений. На рисунке 2.1.1, а показана однородная гладкая пластина при одноосном растяжении. Штриховые силовые линии (траектории напряжения), пересекающие пластину, показывают направления приложенных напряжений

31. Срез и смятие: общая картина деформации при сдвиге, закон Гука, условие прочности.Касательные напряжения вызывают угловые деформации, причем при малых деформациях они не влияют на изменение линейных размеров, и следовательно, на линейные деформации. Поэтому они справедливы также в случае произвольного напряженного состояния и выражают так называемый обобщенный закон Гука.Угловая деформация обусловлена касательным напряжением , а деформации и — соответственно напряжениями и . Между соответствующими касательными напряжениями и угловыми деформациями для линейно-упругого изотропного тела существуют пропорциональные зависимости
которые выражают закон Гука при сдвиге. Коэффициент пропорциональности G называется модулем сдвига. Существенно, что нормальное напряжение не влияет на угловые деформации, так как при этом изменяются только линейные размеры отрезков, а не углы между ними (рис. 1).Линейная зависимость существует также между средним напряжением (2.18), пропорциональным первому инварианту тензора напряжений, и объемной деформацией (2.32), совпадающей с первым инвариантом тензора деформаций:	(7)

 

Рис.2. Плоская деформация сдвигаСоответствующий коэффициент пропорциональности К называется объемным модулем упругости. Чистым сдвигом называют такое напряженное состояние, когда на гранях выделенного из бруса элемента действуют только касательные напряжения. Такие грани называются площадками чистого сдвига.Величина - абсолютный сдвиг, - относительный сдвиг.С деформацией сдвига мы встречаемся при резании ножницами металла, при работе различных соединений (резьбовых, шлицевых, шпоночных).Условие прочности при сдвиге (срезе) имеет вид .

32. Срез и смятие: общая картина деформации при смятии, условие прочности, допускаемые напряжения Деформация смятия явл. разновидностью деформации сжатия при действии силы на небольшой площади. Возникают напряжения, называющиеся напряжения смятия.1) условие прочности на смятие будет иметь вид:

Смятие материала может происходить в местах сочленения отдельных элементов конструкции. Расчет на смятие необходимо проводить как для разъемных, так и неразъемных соединений; стыковочных узлов, заклепочных соединений, сочленений тяг управления.
Напряжение смятия определяется делением силы на площадь контакта, а для отверстий - на проекцию этой площади:

Величина допустимых напряжений смятия 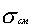зависит от материала и вида соединения. Для неразъемных заклепочных соединений из деформируемых алюминиевых сплавов можно принять 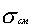=6000 кгс/см2. Для узлов, выполненных из стали, обычно принимают:
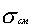=1,3* -в случае неподвижных соединений;
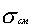=0,65* -в случае малоподвижных соединений;
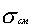=0,2* -в случае подвижных соединений.

33. Расчет заклепок на смятие и листов на разрыв. На практике целый ряд деталей и элементов конструкций работает в таких условиях, что внешние силы стремятся их разрушить именно путем сдвига. В соответствии с этим при проверке прочности таких элементов на первый план выступают касательные напряжения. Простейшими примерами подобных деталей являются болтовые и заклепочные соединения. Заклепки во многих случаях уже вытеснены сваркой; однако они имеют еще очень большое применение для соединения частей всякого рода металлических конструкций: стропил, ферм мостов, кранов, для соединения листов в котлах, судах, резервуарах и т. п. Для образования заклепочного соединения в обоих листах просверливают или продавливают отверстия. В них закладывается нагретый до красного каления стержень' заклепки с одной головкой; другой конец заклепки расклепывается ударами специального молотка или давлением гидравлического пресса (клепальной машины) для образования второй головки. Мелкие заклепки (малого диаметра — меньше 8 мм) ставятся в холодном состоянии (авиационные конструкции).Любое заклепочное соединение работает на 4 вида деформации:-срез заклепок;-срез листа;-разрыв листа;-смятие заклепок;Условия прочности по каждому из видов:1) условие прочности заклепки на перерезывание в таком виде: 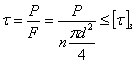Помимо среза заклепкам и соединяемым листам в конструкции угрожают и иные опасности.На рис.1 указана примерная схема передачи давлений на стержень заклепки. Закон распределения этих давлений по цилиндрической поверхности нам неизвестен; он во многом зависит от неправильностей формы заклепочного отверстиями стержня, вызванных условиями изготовления конструкции. Поэтому расчет производится условно. Принято считать, что неравномерное давление, передающееся на поверхность заклепки от листа, распределяется равномерно по диаметральной плоскости сечения заклепки. При этом напряжение по этой диаметральной плоскости оказывается примерно равным наибольшему сминающему напряжению в точке А поверхности заклепки.

Рис.1. Передача давлений на стержень заклепки.Чтобы вычислить это условное напряжение смятия, необходимо разделить силу, приходящуюся на заклепку, на площадь диаметрального сечения ВСС'В'. Эта площадь представляет собой прямоугольник, одной стороной которого служит диаметр заклепки, другая же равна толщине листа, передающего давление на стержень заклепки.

34. практические расчёты сварных соединений. При изготовлении металлических конструкций часто применяется сварка с помощью электрической дуги.Сущность электросварки по методу Славянова заключается в том, что, расплавляя электрической дугой материал электрода (сталь), заполняют им стык соединяемых элементов, также прогреваемых дугой до температуры плавления. В результате, после остывания расплавленного металла, образуется шов, прочно соединяющий стыкуемые элементы.Для защиты плавящегося металла от попадания вредных включений из окружающего воздуха на поверхность электрода наносится толстая защитная обмазка, выделяющая при плавлении электрода большое количество шлака и газов, благодаря чему плавящийся металл изолируется от окружающего воздуха.Этим обеспечивается высокое качество металла сварного шва, механические свойства которого могут резко ухудшиться под влиянием кислорода и азота воздуха (при отсутствии обмазки или при тонкой обмазке). С той же целью автоматическая сварка производится под слоем флюса, защищающим плавящийся металл от попадания кислорода и азота воздуха. Таблица. Допускаемые напряжения при сварке.

Проверка прочности производится на растяжение или сжатие по формуле:

Здесь —условная рабочая площадь сечения шва, где расчетная длина шва , а высота шва h принимается равной толщине свариваемых элементов t. Проверка прочности косых швов производится и по нормальным и по касательным напряжениям, возникающим по сечению шва mn: Имея в виду, что получим:

(10.10)

Здесь расчетная длина шва по техническим условиям принимается равной .Как установлено опытом, наиболее рациональным углом наклона шва к линии действия сил является . Недостатком соединения косым швом является неудобство центрировки стыкуемых элементов при сварке, поэтому его применяют редко.

35. Кручение: общая картина деформации: скручивающие и крутящие моменты, эпюра крутящих моментов. Кручением называется такой вид деформации, при котором в поперечном сечении стержня возникает лишь один силовой фактор — крутящий момент М_z. Крутящий момент по определению равен сумме моментов внутренних сил относительно продольной оси стержня Oz. Нормальные силы, параллельные оси Oz, вклада в крутящий момент не вносят. С силами, лежащими в плоскости поперечного сечения стержня (интенсивности этих сил — касательные напряжения и ) М_z связывает вытекающее из его определения уравнение равновесия статики (рис. 1) Для определения крутящих моментов в сечениях пользуются методом сечений. Намечают участки бруса, рассекают его вооброжаемой плоскостью, мысленно отрбрасывают одну часть. К другой части прикладывают в сечении неизвестный крутящий момент, направляя его по ходу часовой стрелки и составляют уравнение равновесия, из которого находят значение Т.Положительными принимают скручивающие моменты, если они поворачивают отсеченную часть бруса против хода часовой стрелки. Знак крутящего момента бруса значения не имеет.Условимся считать M_z положительным, если со стороны отброшенной части стержня видим его направленным против часовой стрелки (рис. 2). Это правило проиллюстрировано на рис. 1 и в указанном соотношении, где крутящий момент М_z принят положительным. Численно крутящий момент равен сумме моментов внешних сил, приложенных к отсеченной части стержня, относительно оси Ог Кручением называется простой вид сопротивления, при котором к брусу (валу) прикладываются внешние пары сил в плоскостях, совпадающих с поперечным сечением вала, а в последних возникает только внутренний крутящий момент.Рассмотрим расчетную схему вала, нагруженного двумя сосредоточенными моментами М и 2М и распределенными по длине: m, рис.2.Методика построения эпюры аналогична только что рассмотренной методике при растяжении-сжатии.

36. Кручение: напряжение в брусе круглого поперечного сечения, эпюра напряжений. Рассмотрим кручение призматических стержней кругового поперечного сечения. Исследование деформаций упругого стержня с нанесенной на его поверхности ортогональной сеткой рисок (рис. 3) позволяет сформулировать следующие предпосылки теории кручения этого стержня:поперечные сечения остаются плоскими (выполняется гипотеза Бернулли);

1. расстояния между поперечными сечениями не изменяются, следовательно ;

2. контуры поперечных сечений и их радиусы не деформируются. Это означает, что поперечные сечения ведут себя как жесткие круговые пластинки, поворачивающиеся при деформировании относительно оси стержня Ог. Отсюда следует, что любые деформации в плоскости пластинки равны нулю, в том числе и ;

3. материал стержня подчиняется закону Гука. Учитывая, что , из обобщенного закона Гука в форме получаем . Это означает, что в поперечных сечениях, стержня возникают лишь касательные напряжения , а вследствие закона парности касательных напряжений, равные им напряжения действуют и в сопряженных продольных сечениях. Следовательно напряженное состояние стержня — чистый сдвиг.

Выведем формулу для касательных напряжений при кручении призматического стержня кругового поперечного сечения. Как видно, поворот правого торцевого сечения относительно неподвижного левого на угол (назовем его углом закручивания стержня) вызывает поворот продольных волокон на угол (угол сдвига), поскольку на величину искажаются угл ⇐ Предыдущая123 Поделиться: Воспользуйтесь поиском по сайту: ©2015 - 2024 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...