 |
Декартово произведение множеств
|
|
|
|
ТЕОРИЯ МНОЖЕСТВ
Определения
1. Множество A – совокупность элементов, объединённых каким-нибудь общим свойством.
2. xÎA – элемент x принадлежит множеству A.
3. xÏA – элемент x не принадлежит множеству A.
4. Æ – пустое множество.
5. B является подмножеством A, BÍA Û (xÎB Þ xÎA), т.е. каждый элемент xÎB обладает свойством xÎA.
6. "A ÆÍA, т.е. Æ является подмножеством любого множества.
7. Множества A и B равны, A=B Û (AÍB & BÍA).
8. B является строгим подмножеством A, BÌA Û (BÍA & B¹A).
9. B является собственным подмножеством A Û (BÍA & B¹A & B¹Æ).
10. Операции над множествами:
- объединение множеств A и B:
= { x: xÎA или xÎB}
- пересечение множеств A и B:
AÇB = { x: xÎA и xÎB}
- разность множеств A и B:
A \ B = { x: xÎA и xÏB }
- симметрическая разность множеств A и B:
ADB = (A \ B)È(B \ A)
- дополнение множества A относительно U, AÍU:
 = U \ A
= U \ A
Следует обратить внимание:
1. При доказательстве включения AÍB использовать следующую схему доказательства:
«Пусть xÎA, тогда..., значит xÎB. Следовательно, AÍB.»
либо использовать элементарные соотношения типа:
(1) AÇB Í A, AÇB Í B
(2) A Í AÈB, B Í AÈB
(3) A \ B Í A
(4) A Í B и B Í C Þ A Í C
и т.д.
2. При доказательстве равенства двух множеств нужно проверять два включения (см. определение равенства).
3. Правильно пользоваться отрицанием условий:
xÏAÈB Û xÏA и xÏB
xÏAÇB Û xÏA или xÏB
xÏA \ B Û xÏA или xÎB
Примеры решения задач
1. Доказать равенство множеств: AÈB = AÈ(B \ A).
Решение.
Докажем, что AÈB Í AÈ(B \ A).
Пусть xÎAÈB, тогда xÎA или xÎВ.
Если xÎA, то по формуле (2) xÎAÈ(B \ A).
|
|
|
Если xÏA и xÎВ, то по определению разности множеств xÎ(B \ A). По формуле (2) xÎAÈ(B \ A).
Докажем, что AÈB Ê AÈ(B \ A).
Пусть xÎAÈ(B \ A), тогда xÎA или xÎ(B \ A).
Если xÎA, то по формуле (2) xÎAÈB.
Если xÎ(B \ A), то по определению разности множеств xÎB и xÏA. Так как xÎB, то по формуле (2) xÎAÈB.
2. Доказать: AÍBÇC Û AÍB и AÍC
Решение.
Докажем, что AÍBÇC Þ AÍB и AÍC.
Способ 1.
Чтобы доказать, что AÍB и AÍC, возьмем xÎA. Так как AÍBÇC, то из xÎA следует, что xÎB и xÎC. Значит, одновременно выполняются (xÎA и xÎB)и (xÎA и xÎC). Поэтому AÍB и AÍC.
Способ 2.
Учитывая соотношение (1) имеем: AÍBÇCÍB и AÍBÇCÍС. Отсюда по транзитивности получаем: AÍB и AÍC.
Докажем, что AÍBÇC Ü AÍB и AÍC.
Чтобы доказать, что AÍBÇC, возьмем xÎA. Так как AÍB и AÍC, то из xÎA следует, что xÎB и xÎC. По определению пересечения множеств получаем, что xÎ BÇC.
3. Существуют ли такие множества А, В и С, что AÇB ¹ Æ, AÇС = Æ, (AÇB) \ С = Æ?
Если существуют, то привести пример. Если не существуют, то доказать это.
Решение.
Докажем от противного, что таких множеств не существует.
Предположим, что существуют множества А, В и С, удовлетворяющие условию задачи.Так как AÇB ¹ Æ, то существует xÎAÇB, то есть xÎA и xÎB. Поскольку xÎA и по условию AÇС = Æ,то xÏС. Так как xÏС и xÎAÇB, то по определению разности множеств xÎ(AÇB) \ С. Значит, (AÇB) \ С ¹ Æ, чтопротиворечит условию задачи. Следовательно, таких множеств не существует.
4. Доказать равенство множеств А \ (А \ В) = АÇВ.
Решение.
xÎА \ (А \ В) Û
xÎА и xÏ А \ В Û
xÎА и (xÏА или xÎВ) Û
xÎА и xÎВ Û
xÎАÇВ.
Задачи для самостоятельного решения:
1. Доказать: AÈBÍС Û AÍС и BÍС.
2. AÇ(BÈC) = (AÇB)È(AÇC).
|
|
|
3. AÈ (BÇC) = (AÈ B)Ç(AÈ C).
4. Законы де Моргана для AÍU, BÍU:
(a)  =
= 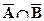 .
.
(b) 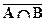 =
= 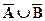 .
.
ДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВ
Определения
1. Мощность множества B – это число его элементов, обозначается |B|.
2. Мощность множества всех подмножеств множества A равна: |P(A)| = 2|A|.
3. Декартово произведение множеств A и B: A´B = { (x, y): xÎA и yÎB}.
4. Мощность декартова произведения множеств A и B равна: |A´B| = |A|×|B|.
Пример 1.
Пусть A={1, 2, 3}, B={a, b}. Тогда декартовы произведения:
A´B = { (1, a), (1, b), (2, a), (2, b), (3, a), (3, b) },
B´A = { (a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3) }.
Видно, что A´B ¹ B´A.
Мощности: |A´B| = |B´A| = 3×2=6.
Пример 2.
Пусть A=[-1, 2], B=[1, 3] – отрезки прямых. Тогда декартово произведение A´B – это все точки (пары координат) прямоугольника:

Примеры решения задач
1. Доказать равенство множеств: (AÈB)´С=(A´C) È (B´C)
Решение.
Докажем, что (AÈB)´СÍ(A´C) È (B´C).
Пусть zÎ(AÈB)´С, тогда z=(x, y), где xÎAÈB и yÎС. Значит, xÎA или xÎВ. То есть xÎA и yÎС или xÎВ и yÎС. Поэтому zÎA´C или zÎB´C. По определению объединения zÎ(A´C) È (B´C).
Докажем, что (AÈB)´С Ê (A´C) È (B´C).
Пусть zÎ(A´C)È(B´C), тогда zÎA´C или zÎB´C. Так как z=(x, y), то xÎA, yÎС или xÎB, yÎС. Значит, xÎA или xÎВ при yÎС. Поэтому xÎAÈB и yÎС. По определению декартова произведения zÎ(AÈB)´С.
|
|
|


