Главная | Обратная связь | Поможем написать вашу работу!

Бинарные отношения, функции, порядок.

Определения

1. Бинарным отношением между элементами множеств А и В называется любое подмножество декартова произведения RÍA´B, RÍA´А.

2. Если А=В, то R – это бинарное отношение на A.

3. Обозначение: (x, y)ÎR Û xRy.

4. Область определения бинарного отношения R – это множество d_R= {x: существует y такое, что (x, y)ÎR }.

5. Область значений бинарного отношения R – это множество r_R= {y: существует x такое, что (x, y)ÎR }.

6. Дополнение бинарного отношения R между элементами А и В – это множество -R = (A´B) \ R.

7. Обратное отношение для бинарного отношения R – это множество R^-1= {(y, x): (x, y)ÎR}.

8. Произведение отношений R₁ÍA´B и R₂ÍB´C – это отношение R₁ × R₂ = { (x, y): существует zÎB такое, что (x, z)ÎR₁ и (z, y)ÎR₂ }.

9. Отношение f называется функцией из А в В, если выполняется два условия:

а) d_f= А, r_fÍ В

б) для всех x, y₁, y₂ из того, что (x, y₁)Îf и (x, y₂)Îf следует y₁=y₂.

10. Отношение f называется функцией из А на В, если в первом пункте будет выполняться d_f= А, r_f= В.

11. Обозначение: (x, y)Îf Û y = f(x).

12. Тождественная функция i_A: A®A определяется так: i_A(x) = x.

13. Функция f называется 1-1 -функцией, если для любых x₁, x₂, y из того, что y = f(x₁) и y = f(x₂) следует x₁=x₂.

14. Функция f: A®B осуществляет взаимно однозначное соответствие между А и В, если d_f= А, r_f= В и f является 1-1-функцией.

15. Свойства бинарного отношения R на множестве А:

- рефлексивность: (x, x)ÎR для всех xÎA.

- иррефлексивность: (x, x)ÏR для всех xÎA.

- симметричность: (x, y)ÎR Þ (y, x)ÎR.

- антисимметричность: (x, y)ÎR и (y, x)ÎR Þ x=y.

- транзитивность: (x, y)ÎR и (y, z)ÎR Þ (x, z)ÎR.

- дихотомия: либо (x, y)ÎR, либо (y, x)ÎR для всех xÎA и yÎA.

16. Множества А₁, A₂,..., А_r из Р(А) образуют разбиение множества А, если

- А_i¹ Æ, i = 1,..., r,

- A = A₁ÈA₂È...ÈA_r,

- A_iÇA_j= Æ, i ¹ j.

Подмножества А_i, i = 1,..., r, называются блоками разбиения.

17. Эквивалентность на множестве А – это рефлексивное, транзитивное и симметричное отношение на А.

18. Класс эквивалентности элемента x по эквивалентности R – это множество [x]_R={y: (x, y)ÎR}.

19. Фактор множество A по R – это множество классов эквивалентности элементов множества А. Обозначение: A/R.

20. Классы эквивалентности (элементы фактор множества А/R) образуют разбиение множества А. Обратно. Любому разбиению множества А соответствует отношение эквивалентности R, классы эквивалентности которого совпадают с блоками указанного разбиения. По-другому. Каждый элемент множества А попадает в некоторый класс эквивалентности из A/R. Классы эквивалентности либо не пересекаются, либо совпадают.

21. Предпорядок на множестве A – это рефлексивное и транзитивное отношение на А.

22. Частичный порядок на множестве A – это рефлексивное, транзитивное и антисимметричное отношение на А.

23. Линейный порядок на множестве A – это рефлексивное, транзитивное и антисимметричное отношение на А, удовлетворяющее свойству дихотомии.

Пример 1.

Пусть A={1, 2, 3}, B={a, b}. Выпишем декартово произведение: A´B = { (1, a), (1, b), (2, a), (2, b), (3, a), (3, b) }. Возьмём любое подмножество этого декартова произведения: R = { (1, a), (1, b), (2, b) }. Тогда R – это бинарное отношение на множествах A и B.

Будет ли это отношение являться функцией? Проверим выполнение двух условий 9a) и 9б). Область определения отношения R – это множество d_R= {1, 2} ¹ {1, 2, 3}, то есть первое условие не выполняется, поэтому в R нужно добавить одну из пар: (3, a) или (3, b). Если добавить обе пары, то не будет выполняться второе условие, так как a¹b. По этой же причине из R нужно выбросить одну из пар: (1, a) или (1, b). Таким образом, отношение R¢ = { (1, a), (2, b), (3, b) } является функцией. Заметим, что R¢ не является 1-1 функцией.

На заданных множествах A и В функциями также будут являться следующие отношения: { (1, a), (2, a), (3, a) }, { (1, a), (2, a), (3, b) }, { (1, b), (2, b), (3, b) } и т.д.

Пример 2.

Пусть A={1, 2, 3}. Примером отношения на множестве A является R = { (1, 1), (2, 1), (2, 3) }. Примером функции на множестве A является f = { (1, 1), (2, 1), (3, 3) }.

Примеры решения задач

1. Найти d_R, r_R, R^-1, R×R, R×R^-1, R^-1×R для R = {(x, y) | x, y Î D и x+y£0}.

Решение.

Если (x, y)ÎR, то x и y пробегают все действительные числа. Поэтому d_R = r_R = D.

Если (x, y)ÎR, то x+y£0, значит y+x£0 и (y, x)ÎR. Поэтому R^-1=R.

Для любых xÎD, yÎD возьмём z=-|max(x, y)|-1, тогда x+z£0 и z+y£0, т.е. (x, z)ÎR и (z, y)ÎR. Поэтому R×R = R×R^-1 = R^-1×R = D².

2. Для каких бинарных отношений R справедливо R^-1= -R?

Решение.

Пусть RÍA´B. Возможны два случая:

(1) AÇB¹Æ. Возьмём xÎAÇB. Тогда (x, x)ÎR Û (x, x)ÎR^-1Û (x, x)Î-R Û (x, x)Î(A´B) \ R Û (x, x)ÏR. Противоречие.

(2) AÇB=Æ. Так как R^-1ÍB´A, а -RÍA´B, то R^-1= -R= Æ. Из R^-1= Æ следует, что R = Æ. Из -R = Æ следует, что R=A´B. Противоречие.

Поэтому если A¹Æ и B¹Æ, то таких отношений R не существует.

3. На множестве D действительных чисел определим отношение R следующим образом: (x, y)ÎR Û (x–y) – рациональное число. Доказать, что R есть эквивалентность.

Решение.

Рефлексивность:

Для любого xÎD x-x=0 – рациональное число. Потому (x, x)ÎR.

Симметричность:

Если (x, y)ÎR, то x-y = . Тогда y-x=-(x-y)=- – рациональное число. Поэтому (y, x)ÎR.

Транзитивность:

Если (x, y)ÎR, (y, z)ÎR, то x-y = и y-z = . Складывая эти два уравнения, получаем, что x-z = + – рациональное число. Поэтому (x, z)ÎR.

Следовательно, R – это эквивалентность.

4. Разбиение плоскости D² состоит из блоков, изображённых на рисунке а). Выписать отношение эквивалентности R, соответствующее этому разбиению, и классы эквивалентности.

Аналогичная задача для b) и c).

Решение.

а) две точки эквивалентны, если лежат на прямой вида y=2x+b, где b – любое действительное число.

b) две точки (x₁,y₁) и (x₂,y₂) эквивалентны, если (целая часть x₁ равна целой части x₂) и (целая часть y₁ равна целой части y₂).

с) решить самостоятельно.

Задачи для самостоятельного решения:

1. Доказать, что если f есть функция из A в B и g есть функция из B в C, то f×g есть функция из A в C.

2. Пусть A и B – конечные множества, состоящие из m и n элементов соответственно.

a) Сколько существует бинарных отношений между элементами множеств A и B?

b) Сколько имеется функций из A в B?

c) Сколько имеется 1-1 функций из A в B?

d) При каких m и n существует взаимно-однозначное соответствие между A и B?

3. Доказать, что f удовлетворяет условию f(AÇB)=f(A)Çf(B) для любых A и B тогда и только тогда, когда f есть 1-1 функция.

КОМБИНАТОРИКА

Произведение всех натуральных чисел от 1 до n обозначается:

n! = 1·2·3·…·(n-1)·n, 0! = 1

Пусть X={x₁, x₂,..., x_n} – это множество из n элементов, k £ n.

Размещение элементов из X объёма k – это упорядоченное подмножество из k элементов, принадлежащих X.

Количество размещений объёма k из n различных элементов с неограниченными повторениями:

= n^k (знач^мест)

Если на каждую i -ю из k позиций можно поставить один из q_i элементов множества X, то количество таких размещений равно:

(q₁, q₂,..., q_n) = q₁ × q₂ ×... × q_n

Количество размещений объёма k из n различных элементов без повторений:

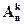= n (n - 1)(n - 2) … (n - k + 1)=

Перестановка элементов из X – это размещение элементов из X объёма n.

Количество перестановок из n различных элементов:

= P_n = n!

Если n элементов содержат q_i элементов i -го сорта, q₁ + q₂ +... + q_m = n и элементы одного сорта идентичны, то число перестановок равно:

P_n(q₁, q₂,..., q_m) =

Сочетание элементов из X объёма k – это неупорядоченное подмножество из k элементов, принадлежащих X.

Сочетания, размещения и перестановки могут быть также с повторениями элементов множества X (неограниченными и ограниченными).

Количество сочетаний объёма k из n различных элементов без повторений:

Количество сочетаний объёма k из n различных элементов с неограниченными повторениями:

Бином Ньютона:

Свойства:

(1)

(2)

(3)

(4)

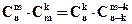
(5)

При решении комбинаторных задач часто используются следующие правила комбинаторики:

Правило суммы. Если объект А может быть выбран n способами, а объект B другими m способами, то выбор «либо А, либо В» может быть осуществлен n+m способами.
Правило произведения. Если объект А может быть выбран n способами и после каждого из таких выборов объект B в свою очередь может быть выбран m способами, то выбор «A и B» в указанном порядке может быть осуществлен n×m способами.

Задача-пример. Из 12 девушек и 10 юношей выбирают команду, состоящую из пяти человек. Сколькими способами можно выбрать эту команду так, чтобы в нее вошло не более трех юношей?

Решение. Условие «не более трех» означает, что в команду может входить либо 3 юноши, либо 2 юноши, либо 1 юноша, либо ни одного юноши. Таким образом, в задаче выделяются четыре различных случая. В соответствии с правилом сложения нужно подсчитать количества вариантов в каждом из этих случаев и сложить их.

Рассмотрим первый случай. Нужно подсчитать, сколькими способами можно выбрать из 12 девушек и 10 юношей команду, состоящую из 3х юношей и 2х девушек. Из 10 юношей можно выбрать 3х юношей способами. Для каждых трех выбранных юношей можно выбрать также способами 2х девушек из 12ти. Поэтому работает правило умножения и в первом случае число вариантов команд равно × .

Аналогично, во втором случае: × .

В третьем случае: × .

В четвертом случае: .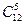

Окончательный ответ: × + × + × + .

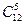Примеры решения задач

№1.17. n (n>2) человек садятся за круглый стол. Два размещения по местам будем считать совпадающим, если каждый человек имеет одних и тех же соседей в обоих случаях. Сколько существует способов сесть за стол?

Решение.

Общее количество всевозможных рассадок равно числу перестановок из n элементов P_n = n! Однако из этих рассадок нужно исключить совпадающие. Отношение соседства сохраняется при циклических перестановках (их n штук) и при симметрическом отражении (их также n штук):

Поэтому всего способов (делить, т.к. правило умножения)

№1.19. Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется хотя бы один туз?

Решение.

Всего способов вынуть 10 карт из колоды . Из них в случаях в выборке не окажется ни одного туза. Поэтому ответ – .

№1.20. Сколькими способами можно составить три пары из n шахматистов?

Решение.

Сначала выберем из n шахматистов 6 человек. Это можно сделать способами. Теперь каждую шестёрку будем разбивать на пары. Для этого поставим 6 шахматистов в ряд, считая, что они имеют имена: a, b, c, d, e, f. Это можно сделать 6! способами. Однако нам не важен порядок внутри каждой пары и порядок самих пар. Перестановок, в которых шахматисты меняются местами в парах 2³. Перестановок, в которых меняются местами пары 3!. Поэтому разбить на пары 6 шахматистов можно способами. Ответ .

№1.24. Сколько существует чисел от 0 до 10ⁿ, в которые не входят две идущие друг за другом одинаковые цифры?

Решение.

Рассмотрим все n-значные числа. Первую цифру мы можем выбрать 9-ю способами. Чтобы вторая цифра была отлична от первой, то её также можно выбрать 9-ю способами. Количество таких n-значных чисел равно количеству размещений объёма n из 9 элементов с неограниченными повторениями, т.е. равна 9ⁿ для n>1 и 10 для n=1.

Поэтому ответ 10+9²+9³+...+9ⁿ. Число 10ⁿ не подходит.

ТЕОРИЯ АЛГОРИТМОВ

· Пусть N – это множество натуральных чисел, включая нуль.

· В данном разделе курса будут рассматриваться функции многих переменных fⁿ(x₁,..., x_n), определенные на некотором множестве MÍNⁿ c натуральными значениями, т.е. fⁿ(x₁,..., x_n)ÎN, x_iÎN для i=1,..., n, или fⁿÍ Nⁿ⁺¹.

· Функция fⁿ(x₁,..., x_n) называется всюду определенной, если её областью определения является Nⁿ, т.е. для любого набора из n натуральных чисел существует натуральное число, являющееся значением функции fⁿ.

· Простейшие всюду определенные функции:

1. s(x)=x+1 для любого x;

2. o(x)=0 для любого x;

3. Iⁿ_m(x₁,..., x_m,..., x_n)=x_m.

Эти простейшие функции всюду определены и из них с помощью конечного числа применений операторов, введенных ниже, можно конструировать более сложные функции.

· Оператор суперпозиции:

Функция hⁿ(x₁,..., x_n) получается из функций g^m, fⁿ₁,..., fⁿ_m с помощью оператора суперпозиции, если hⁿ(x₁,..., x_n) = g^m(fⁿ₁(x₁,..., x_n),..., fⁿ_m(x₁,..., x_n)).

· Оператор примитивной рекурсии:

Функция fⁿ⁺¹(x₁,..., x_n, y) получается из функций gⁿ(x₁,..., x_n) и hⁿ⁺²(x₁,..., x_n, y, z) с помощью оператора примитивной рекурсии, если она может быть задана схемой примитивной рекурсии:

æfⁿ⁺¹(x₁,..., x_n, 0) = gⁿ(x₁,..., x_n),

èfⁿ⁺¹(x₁,..., x_n, y+1) = hⁿ⁺²(x₁,..., x_n, y, fⁿ⁺¹(x₁,..., x_n, y)).

· Оператор минимизации:

Функция fⁿ(x₁,..., x_n) получается из функции gⁿ⁺¹(x₁,..., x_n, y) с помощью оператора минимизации и обозначается fⁿ(x₁,..., x_n)=my[gⁿ⁺¹(x₁,..., x_n, y)=0], если:

fⁿ(x₁,..., x_n) определено и равно y Û gⁿ⁺¹(x₁,..., x_n, 0),..., gⁿ⁺¹(x₁,..., x_n, y-1) определены и не равны нулю, а gⁿ⁺¹(x₁,..., x_n, y)=0.

(Можно говорить также: «Функция fⁿ(x₁,..., x_n) равна минимальному значению y, при котором функция gⁿ⁺¹ обращается в нуль»)

· Примитивно рекурсивная функция (прф)

Функция fⁿ⁺¹(x₁,..., x_n, y) называется примитивно рекурсивной, если она может быть получена из простейших функций с помощью конечного числа применений операторов суперпозиции и примитивной рекурсии.

Следует отметить, что все примитивно рекурсивные функции всюду определены.

· Частично рекурсивная функция (прф)

Функция fⁿ⁺¹(x₁,..., x_n, y) называется частично рекурсивной, если она может быть получена из простейших функций с помощью конечного числа применений операторов суперпозиции, примитивной рекурсии и минимизации.

· Из определений легко заметить, что примитивно рекурсивные функции являются также частично рекурсивными. Однако существуют частично рекурсивные функции, не являющиеся примитивно рекурсивными.

Примеры решения задач

1. Доказать, что следующие функции являются примитивно рекурсивными.

a) f(x)=x+n

Решение. Функция f(x) может быть получена с помощью n-кратного применения оператора суперпозиции к простейшей функции s(x).

b) f(x,y)=x+y

Решение. Функция f(x) может быть задана следующей схемой примитивной рекурсии:

æf(x, 0) = x = I¹₁(x),

èf(x, y+1) = x+y+1=f(x,y)+1=s(f(x,y))=s(I³₃(x,y,f(x,y))).

Здесь функция g(x) имеет вид g(x)= I¹₁(x) и является, как и полагается, функцией одной переменной. А функция h(x,y,z) имеет вид h(x,y,z)=s(I³₃(x,y,z)) и является функцией трех переменных.

Заметим, что функции g(x) и h(x,y,z) являются прф, т.к. g(x) – третья простейшая функция, а h(x,y,z) может быть получена из простейших функций s(x) и I³₃(x,y,z) с помощью применения оператора суперпозиции.

Так как функцию f(x,y) можно получить с помощью оператора примитивной рекурсии из примитивно рекурсивных функций g(x) и h(x,y,z), то f(x,y) – прф.

с) f(x,y)=xy

Решение. Функция f(x) может быть задана следующей схемой примитивной рекурсии:

æf(x, 0) = 0 = o(x),

èf(x, y+1) = x(y+1)=xy+x=f(x,y)+x= I³₃(x,y,f(x,y)))+ I³₁(x,y,f(x,y))).

Так как функцию f(x,y) можно получить с помощью оператора примитивной рекурсии из примитивно рекурсивных функций g(x)=o(x) и h(x,y,z) = I³₃(x,y,z)) + I³₁(x,y,z)), то f(x,y) – прф.

2. Пусть g(x₁,..., x_n,y) примитивно рекурсивная функция. Доказать, что следующая функция примитивно рекурсивна:

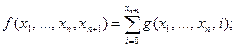
Решение. Особенность этой функции заключается в том, что суммирование ведется по переменному числу слагаемых. Однако функция fⁿ⁺¹ может быть задана следующей схемой примитивной рекурсии:

æf(x₁,..., x_n, 0) = g(x₁,..., x_n,0) – прф,

èf(x₁,..., x_n, y+1) = = f(x₁,..., x_n, y) + g(x₁,..., x_n,y+1) – сумма прф g и самой функции f.

3. Доказать, что следующая функция частично рекурсивна.

Решение. Покажем, что функция f(x,y) может быть получена с помощью оператора минимизации.

Пусть x³y, тогда f(x,y) определена и принимает некоторое значение: f(x,y) = x-y = z. Как вычислить z? Можно предложить следующий способ: начиная с нуля перебирать по порядку все значения z, пока не выполнится условие x-y=z, или x-y-z=0. Такое z обязательно найдется, т.к. x-y³0. Если же x-y<0, то ни какое натуральное z не подойдет.

Программист записал бы это так:

unsigned int f(x,y)

{

z=0;

while((x-y-z)!=0) z++;

return z;

}

То же самое можно записать и в терминах оператора минимизации:

f(x, y)=mz[|x–y–z|=0]

Модуль необходим для того, чтобы функция g(x,y,z)=|x–y–z| была определена, даже если x–y<0. Заметим, что g(x,y,z)=|x–y–z| является примитивно рекурсивной, т.к. может быть получена с помощью конечного числа применений оператора суперпозиции к простейшим функциям.

Поэтому f(x,y) – чрф.

Задачи для самостоятельного решения:

1. Доказать, что следующие функции являются примитивно рекурсивными.

a) f(x,y) = x^y (здесь 0⁰=1);

b) f(x,y) = x! (здесь 0!=1);