Контрольно-измерительные средства

Образец первого рубежного контроля

1. Какой знак вместо символа «?» нужно подставить в выражение, чтобы получить верное утверждение? а) {3}? {1,3,5}; b) {1,3}? {1,3,5}; c) 0? {1,3,5}; d) 3? {1,3,5}. 2. Данное множество задать перечислением элементов
{х:(х - 2)(x² - 2х + 2) = 0, х R}.

3. Данное множество задать общим свойством {2,4,6,8, • • •,22}.
4-12. Даны множества А и В: А = {х,у,z,t,и}, В = {г,t,и,v,w}. Найти: 4. , 5. , 6. , 7. , 8. , 9. , 10. . 13. Найти булеан множества А ={p,q,r} или А ={p,q }.

14. Для данных множеств А и В найти их прямое произведение А х В или В х А, если А = {6,7,8}, В = {2,3}.

15. Найти А² = А х А, если А ={c,d,e}.

16- 19. Пусть на множестве А = {p,q,r} задано отношение P={(p,p),(p,q),(q,q),(q,r),(r,q)}. Найти: 16. отношение ; 17. отношение ; 18. матрицу[P] отношения Р;

19. композицию Р о Q, если Q= {(p,1),(p,3), (q,3), (г,4)}.

20-22. Даны матрицы отношений P и Q.Найти: 20. матрицу объединения ; 21. матрицу пересечения ; 22. матрицу композиции .

 

Образец второго рубежного контроля

1.Как называется и читается логическая операция .

2. Как называется логическая операция, найти её таблицу истинности:

3.Найти таблицу истинности формулы: .

4.По данному вектору значений функции Найти её таблицу истинности: .

5. По нулевым наборам функции найти её таблицу истинности: .

6. По единичным наборам функции найти её таблицу истинности: .

7. Найти формулу, эквивалентную формуле по закону ассоциативности.

8. В какой форме из перечисленных ниже записана формула :

а) ДНФ; б) СДНФ; в) СКНФ; г) КНФ.

9. По карте Карно найти СДНФ:

 

 

у

x 1
1

10. По карте Карно найти МДНФ(см.пункт 9).

11. Для данной схемы найти переключательную функцию:

х

у

 

12. По нулевым наборам функции найти её СКНФ.

13. По единичным наборам функции найти её СДНФ.

 

Образец третьего рубежного контроля

1-10. Дан граф

3

b e 4

2

d

a c 5

 

1. Найти матрицу инцидентности.

2. Найти матрицу смежности.

3. Задать граф списком дуг /

4. Найти степень вершины 3.

5. Найти цикломатическое число.

6. Найти матрицу расстояний.

7. Найти эксцентриситет вершины 1.

8. Найти диаметр графа.

9. Найти радиус графа.

10. Перечислить центральные вершины графа.

11-12. Дан взвешенный граф

 

 

A

3 E.

B 5

4 D

С

 

 

11. Найти матрицу весов.

12. Сколько ребер надо удалить из графа, чтобы получить остов (дерево).

13. Ориентированный граф задан множеством вершин и множеством дуг 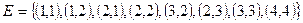. Задать граф графически.

14. Ориентированный граф задан множеством вершин и множеством дуг 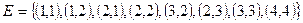. Составить матрицу соответствующего бинарного отношения.

 

Экзаменационные вопросы

1. Множества, их способы задания. Подмножества, булеан. Операции над множествами. Свойства операции над множествами. Разбиения и покрытия множеств.

2. Прямое произведение множеств. Отношения (унарные, бинарные, n-арные). Способы задания бинарных отношений. Обратное отношение, дополнение отношения, тождественное отношение. Композиция бинарных отношений.

3. Основные свойства матриц бинарных отношений. Свойства бинарных отношений (рефлексивность, симметричность, антисимметричность, транзитивность).

4. Отношение эквивалентности. Классы эквивалентности, фактор-множество.

5. Отношение порядка. Лексикографический порядок.

6. Функциональные отношения. Инъекция, сюръекция, биекция. Понятие о мощности множеств.

7. Основные понятия логики высказываний. Высказывание, основные логические операции.

8. Логические переменные и формулы. Таблицы истинности логических операций и формул. Соглашение о приоритетах логических операций.

9. Функции алгебры логики. Способы задания логических функций (таблица истинности, нулевые и единичные наборы, вектор значений, формула).

10. Эквивалентность формул. Основные эквивалентные соотношения алгебры логики.

11. Полные системы логических функций. Приведение логических формул к ДНФ, КНФ.

12. Совершенные ДНФ и КНФ (СДНФ и СКНФ).

13. Минимизация в классе ДНФ. Карты Карно.

14. Коммутационные схемы.

15. Двойственность. Булева алгебра и теория множеств.

16. Основные понятия и определения теории графов (н-граф и орграф, мультиграф, инцидентность, смежность, степени вершин).

17. Способы задания графов (пара множеств , рисунок, матрицы инцидентности и смежности, список ребер (дуг)).

18. Связь между графами и бинарными отношениями. Изоморфизм графов. Подграфы. Операции над графами.

19. Маршруты, цепи, пути, циклы, контуры. Связность, сильная связность, компоненты связности.

20. Определение связных и сильно связных компонент. Матрица достижимости.

21. Исследование маршрутов графа (определение маршрутов фиксированной длины и их количество).

22. Расстояния в графах (эксцентриситет, диаметр, радиус, центр)

23. Взвешенные графы. Матрица весов. Взвешенное расстояние. Нахождение кратчайших маршрутов (алгоритм Дейкстры).

24. Деревья, лес. Корневые деревья. Остов графа. Цикломатическое число. Число остовных деревьев графа (теорема Кирхгофа). Определение остовного дерева минимального веса (алгоритмы Краскаля и Прима).

Рекомендуемая литература

Основная литература

1. Судоплатов С.В., Овчинникова Е.В. Элементы дискретной математики. – М.: ИНФРА-М, Новосибирск: изд-во НГТУ, 2002

2. Новиков Ф.А. Дискретная математика для программистов. – Спб.: Питер, 2001

3. Андерсон Д. Дискретная математика и комбинаторика.: Пер. с англ.-М.:Издательский дом «Вильямс», 2004.

4. Шапорев С.Д. Дискретная математика. Курс лекций и практических занятий.-СПб.:БХВ-Петербург, 2006.

Дополнительная литература

5. Белоусов А.И., Ткачев С.Б. Дискретная математика. – М.: из-во МГТУ им.Н.Э.Баумана, 2001

6. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. – М.: Энергия,1980

7. Мутанов, Г.М.,Акбердин Р.А. Теория графов. – Алматы:, Рауан,1999

8. Капитонова Ю.В. и др. Лекции по дискретной математике. – Спб.: БХВ-Петербург, 2004

9. Горбатов В.А., Фундаментальные основы дискретной математики. - М.: Наука-Физматгиз, 2002

10. Москинова Г.И., Дискретная математика.-М.: Логос,2004

11. Акимов О.Е., Дискретная математика.-М.: ЛБЗ,2001

Разработки кафедры

12. Астраханцева Л.Н., Байсалова М.Ж. Дискретная математика. Метод. указания и задания к выполн. расчетно- графич. работы для студентов всех форм обучения специальности 050704 – Вычислительная техника и программное обеспечение). -Ч.1 -Алматы: АИЭС, 2008.- 16с.

13. Астраханцева Л.Н., Байсалова М.Ж. Дискретная математика. Метод. указания и задания к выполн. расчетно- графич. работы для студентов всех форм обучения специальности 050704 – Вычислительная техника и программное обеспечение). -Ч.2 -Алматы: АИЭС, 2008.- 22с.

14. Астраханцева Л.Н., Байсалова М.Ж. Дискретная математика. Метод. указания и задания к выполн. расчетно- графич. работы для студентов всех форм обучения специальности 050704 – Вычислительная техника и программное обеспечение). -Ч.3 -Алматы: АИЭС, 2008.- 22с.

15. Астраханцева Л.Н. Дискретная математика. Конспект лекций для студентов всех форм обучения специальн. 050704-Вычислительная техника и программное обеспечение, 050703-Информацион. системы.- Алматы:АИЭС, 2008.-57с.

Общие принципы контроля работы студента:

Процесс обучения и контроль знаний базируется на следующей схеме:

1. Входной контроль знаний студентов проводится на дисциплинах «Математика 1», «Математический анализ. Введение в анализ» или «Алгебра и геометрия» в зависимости от специальности.

2. Количество типовых единичных циклов работы преподавателя со студентом (РПС) равно количеству кредитов (КК), выделенных на дисциплину. Например, в дисциплине из трех кредитов выполняется 3 РГР.

3. Программа курса предполагает выполнение в каждом типовом учебном цикле выполнение одной расчетно-графической работы (РГР).

4. Все этапы текущего контроля успеваемости и промежуточной аттестации проводятся в соответствии с положением АУЭС.

Общие принципы текущего контроля и рубежной аттестации:

5. Расчетно-графическая работа выполняется в отдельной ученической тетради. Оценка каждой расчетно-графической работы проводится, исходя из процентного содержания количества решенных и защищенных задач. Их средняя арифметическая есть оценка по этому виду работы, обозначается символом - РГР.

6. Активность работы в аудитории и посещаемость обозначается АЗ.

7. Рубежный контроль (РК) проводится на поточных лекциях или СРСП согласно календарным графикам дисциплины. Рубежный контроль проводится в виде теста открытого типа на бумажном носителе. Каждый рубежный контроль состоит из 16 вопросов.

8. Количество рубежных контролей определяется по формуле: КК-1 (их минимальное количество - 2).

9. Оценка этого вида работы есть средняя арифметическая правильно решенных заданий всех РК по дисциплине в процентном эквиваленте.

10. Ввиду недостаточного уровня математической подготовки в средних школах и адаптационного уровня для допуска на экзамен устанавливается нижний порог в шесть правильно решенных заданий в средней арифметической всех РК.

11. Заключительная рубежная аттестация - компьютерное тестирование (КТ) проводится согласно нормативным актам НАО АУЭС.

Оценка рейтинга допуска

12. Рейтинг допуска (РД) определяется формулой для дисциплин без лабораторных занятий и для дисциплин с лабораторными занятиями:

Нижний порог РД устанавливается согласно нормативам НАО АУЭС.

 

Схема проведения и оценка итогового контроля (промежуточная аттестация):

13. Экзамен проводится в соответствии с положением о проведении экзаменов в НАО АУЭС.

14. Итоговый контроль является комплексным экзаменом и состоит из пяти (5) вопросов: 1 теоретический вопрос + 4 задачи, причем три из них являются аналогом заданий из компьютерных тестов.

15. Срок хранения письменных работ 3 месяца.

16. Экзаменационные работы исправлению не подлежат.

17. Образец бланка экзаменационного билета имеет вид:

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: