 |
Количественный анализ
|
|
|
|
Построение дерева отказов позволяет вникнуть в задачу, так, как это не удается сделать другими средствами, но полностью возможности этого метода не реализуются без количественного анализа. Цель количественного анализа состоит в эффективном распределении бюджета, отведенного на безопасность. Для этого рассматривается влияние различных альтернатив на дерево отказов и его головное событие. Отношение затраты/прибыль является критерием для выбора варианта системы.
Если учесть широкую применимость термина затраты — прибыль, то его значение изложено не совсем ясно. В данном контексте он означает деньги, затраченные на снижение бесполезных затрат. Это станет понятнее, если отделить на время меру затрат от меры прибылей. Затраты определяются как деньги, уплачиваемые за внедрение устройств, методов, процедур и т. д., называемых контрмерами, в промышленную систему в течение заданного интервала времени. Это значит, что затраты на устройства, которые должны периодически обновляться или заменяться, приводятся к средним затратам за заданный интервал времени, например, 1000000 Чел.-ч. Незаменяемые и необновляемые агрегаты, такие как защитные устройства машин, учитываются в терминах срока службы машины. Затраты на обучение определяются в зависимости от частоты проведения занятий. Для сопоставимости все контрмеры должны приводиться к общему знаменателю.
Меры прибыли, трактуемые как ожидаемое сокращение убытков или потерь, требуют более подробного разъяснения. Аварии и несчастные случаи вызывают бесполезные затраты в деньгах или потери трудоемкости. Уровень этих затрат и потерь непосредственно связан с серьезностью аварий. Каждое головное событие анализируемого дерева представляет собой аварию или несчастный случай, серьезность которых может быть непостоянной. С помощью регистрационных записей можно определить частость, с которой головное событие приводит к необходимости оказать первую помощь, временной нетрудоспособности, частичной или полной инвалидности и к смертельному исходу. В.каждом из этих исходов будут свои убытки, указанные в табл. 5.1.
|
|
|
Пример распределения убытков Таблица 5.1
| Номер по классификации | Серьезность аварий | Убыток* Ui |
| Первая помощь | ||
| Временная нетрудоспособность | ||
| Частичная инвалидность | ||
| Полная инвалидность (смертельный исход не учитывается) |
* Эти значения следует оценивать не только в долларах, но и в более трудно измеряемых единицах таких, как социальные убытки. В приведенном примере затраты на первую помощь оценены в долларах на несчастный случай. Все другие значения являются средним на несчастный случай по данным сборника Национального Совета по технике безопасности 1971 г. В общем случае для расчета убытков необходимо учитывать финансовую политику компании.
Ожидаемые потери при появлении головного события могут быть рассчитаны по формуле
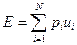 (5.1)
(5.1)
где рi - вероятность появления последствий i-го класса при появления головного события; N - число классов последствий различной серьезности; ui - потери, связанные с i -м классом последствий. Приведенное выражение не определяет абсолютной меры потерь и справедливо только при появлении головного события. Следовательно, величина Е может рассматриваться как ожидаемые затраты при аварии или несчастном случае. Значения uiмогут выражаться в деньгах, потерянных рабочих днях и т. д.
Другим способом определения величины Е мог бы быть учет реальных потерь в прошлом. Пусть, например, потери выражаются в потерянных рабочих днях. Предположим, что в п прошедших появлениях головного события потери составляли u1, u2, … un. Ожидаемые потери можно оценить по среднему арифметическому известных потерь:
|
|
|
 (5.2)
(5.2)
Можно показать, что фактически выражения (5.1) и (5.2) эквивалентны, если считать, что п равно числу классов последствий М, а вероятности появления последствий различных классов равны между собой (рi=1/п). Это происходит, когда мы рассматриваем каждую аварию или несчастный случай как отдельную ситуацию.
Величина Е, задаваемая формулами (5.1) и (5.2), показывает, каких потерь можно ожидать при аварии или несчастном случае, но она никак не связана с затратами на обеспечение безопасности. Чтобы их учесть, надо рассмотреть еще несколько важных факторов. Один из них — частота, с которой происходят аварии. При использовании дерева отказов она выражается в терминах вероятностей. До обсуждения способов расчета вероятности Р появления головного события рассмотрим, как используется эта вероятность.
Величины Е и Р являются абсолютными мерами «критичности» данного головного события, выражаемой в виде
С = РЕ, (5.3}
где С — ожидаемые потери, связанные с появлением головного события в течение данного интервала времени или данной единицы трудоемкости. Покажем это на примере. Предположим, что некоторое головное событие произошло пять раз за последние 100 млн. Чел.-ч. Тогда вероятность Р равна 0,05 или 5% за любые миллион Чел.-ч. Предположим также, что средняя серьезность это-. го события согласно измерениям и формулам (5.1) и (5.2) составляет 8 потерянных человеко-дней. Абсолютная критичность такого головного события С=(0,05 событий/млн. чел.-ч.) • (8 потерянных рабочих дней/число событий = 0,4 рабочих дня/млн. чел.-ч.). Эта мера формируется независимыми частотой и убытками, и поэтому может применяться для сравнения различных головных событий. В качестве единиц времени или продукции и убытков можно использовать любые единицы, а не только млн. чел.-ч и потерянные рабочие дни.
С единицами надо разобраться до начала расчетов. Можно использовать любые единицы, но надо помнить, что количество появлений события в течение выбранной единицы времени трактуется впоследствии как вероятность. Следовательно, вероятностные за.коны должны быть приложены к единицам измерения. Это влияет на масштаб единиц, но т на их физический смысл, В приведенном примере время было выражено в миллионах чел.-ч. Возможно в качестве единиц брать 1000 или 100 чел.-ч. Для формулы (5.3) при определении вероятности Р в приведенном примере единица времени рассматривается как одно испытание (см. разд. 4.2). Следовательно, поскольку событие появляется пять раз за 100 испытаний, то вероятность его появления равна 0,05. Если за единицу принять 1000 чел.-ч, то число испытаний равно 100000, а вероятность — 0,00005. С другой стороны, если в качестве единицы принять 100 млн. чел.-ч., то число испытаний равно одному, а вероятность — пяти.
|
|
|
Это не должно смущать, если правильно понимать смысл одного испытания. Испытание должно определяться так, чтобы событие могло лишь появиться или не появиться. Повторные появления события в одном испытании противоречат предположению о двоичном характере события (см. определение термина «событие»). Это значит, что размер одного испытания должен устанавливаться так, чтобы вероятность более одного появления события была пренебрежимо мала. В то же время нецелесообразно выбирать единицу времени слишком малой, так как ничего, кроме усложнения расчетов, это не дает. При выборе единиц надо пользоваться следующим правилом.
|
|
|


