 |
Интерпретация акустических методов
|
|
|
|
Стандартный акустический метод.
Определение коэффициента пористости. Основа метода определения коэффициента пористости пород - наличие тесной взаимосвязи между величинами Vp (или Δτ) и kп. В однородной и изотропной идеально упругой среде скорость распространения упругих волн определяется значением модуля Юнга Е, коэффициента Пуассона υ, плотностью δп-Плотность пористой среды зависит от коэффициента пористости:
δп = δтв-(δтв- δ3)*kп, (2.2)
Где δтв - плотность твердой фазы, т.е. зерен, слагающих скелет породы;
δз - плотность заполнителя порового пространства.
В горных породах связь между фазами, слагающими породу, недостаточно совершенна. По этой причине зависимость Vp от υ и δп, а следовательно, и от kпотклоняется от закона.
На основании экспериментальных и теоретических исследований сред с несовершенными связями предложен ряд выражений, устанавливающих зависимость скорости (интервального времени) распространения продольных волн от пористости.
Наиболее простые из них следующие:
уравнение среднего времени, полученное М. Вилли, А. Грегори и Л. Гарднером,
Δτп = Δτтв + (Δτ3 - Δτтв)•kп; (2.З.)
уравнение степенной связи, предложенное В.Н. Дахновым,
Δτп = Δτтв+kпmп(Δτз- Δτтв)+kглmгл •(Δτз- Δτтв), (2.4.)
где Δτтв - интервальное время в твёрдой фазе породы; mп и mгл - показатели, зависящие соответственно от структуры и степени цементации коллектора, изменяющиеся от 0,7 до 1,5 и возрастающие с увеличением уплотнения.
В основу уравнений (2.З) и (2.4) положена линейная зависимость между скоростью (или интервальным временем) и пористостью. В них не учитывается влияние горного и пластового давлений, хотя их роль возрастает с уменьшением пористости.
|
|
|
Для пористых сред, содержащих глинистые включения в порах, получено уравнение, позволяющее учитывать особенности упругих свойств изучаемых пород и влияние всестороннего сжатия на скорость упругих волн:
 , (2.5)
, (2.5)
где μ - коэффициент, учитывающий относительное содержание и сжимаемость глинистых частиц; βтв, βп, βз - коэффициенты сжимаемости соответственно твёрдой фазы минералов, слагающих скелет породы, объёма порового пространства и его заполнителя.
Уравнение (2.5) определяет зависимость между скоростью Vpи кппород с совершенной связью между твёрдой и жидкой фазами. Условие совершенства связи хорошо удовлетворяет низкопористым трещинным, трещинно-кавернозным карбонатным коллекторам.
Коэффициент пористости в неглинистых коллекторах можно определить одним из следующих способов.
1. Устанавливают величину kп по экспериментальным зависимостям VP = f(kn),полученным по представительной коллекции керна, с учётом эффективного давления и температуры, характерных для данного разреза.
2. Применяют статистические уравнения, выражающие зависимость интервального времени от пористости и глубины залегания пород, которая служит косвенным показателем термобарических условий изучаемого разреза.
Предложенные способы дают возможность оценивать коэффициент пористости с высокой точностью. При подсчёте запасов предпочитают второй способ, поскольку при использовании статистических уравнений систематические ошибки минимальны.
Погрешность оценок kпи Δτп может быть существенно снижена до (1.5-2%) при использовании данных нескольких методов ГИС,т.е. путем применения уравнений множественной корреляционной связи.
3.Используют уравнения (2.4) с дальнейшим введением поправок за уплотнение (эффективное давление) и нефтегазонасыщенность.Данный способ наиболее распространен на практике. Получают следующее выражение для kп:
|
|
|
kn = (Δτп - Δτтв)/(Δτз- Δτтв), (2.6)
которое справедливо для пород с мономинеральным составом скелета при насыщении пор одним флюидом.
Степень влияния различных параметров, входящих в уравнение (2.6), на точность оценки kпне одинакова, интервальное время в заполнителе порового пространства зависит от состава флюидов и изменяется в зависимости от температуры и давления (глубины залегания). Для водных растворов оно определяется достаточно точно по эмпирическому выражению:
Δτ = 710•(1-1,2-10-3•p)/(1+2,2•10-3-1,65•10-5•t2)•(1+5.5•10-4•Св), (2.7)
где Св - минерализация, кг/м3; р- давление, МПа; t- температура 0С.
Наибольшие ошибки при определении kпвозникают из-за неверной оценки интервального времени в твердой фазе породы, соответствующего скорости Vp при kп —> 0.
Существует несколько способов определения Δτтв:
1. Использование значений Δτтв, полученных для определенных минералов в атмосферных условиях. Однако такой подход в некоторых случаях может привести к значительным погрешностям, поскольку диапазон изменения скоростей в твердой фазе литологически однотипных пород даже при атмосферных условиях довольно широк и может изменяться в зависимости от состояния поверхности зерен и акустического контакта между ними.
2. Линейная экстраполяция зависимости Δτ=f{kп)к нулевой пористости, основанная на сопоставлении скорости, измеренной в скважине, с величинами kп, определенными на керне при сплошном его отборе.
3. Сопоставление интервального времени и удельного электрического сопротивления породы, полученного по результатам записи экранированным зондом. В этом случае по оси абсцисс откладывают Δτп в линейном масштабе, а по оси ординат - значения ρк в масштабе у = ρк –1/2. Интервальное время Δτтв находят в результате экстраполяции полученной зависимости до пересечения с осью ординат в точке ρк >∞. Такой способ рекомендуется использовать для глинистых, нетрещиноватых пород.
Опыт использования уравнения (2.З) показывает, что оно дает удовлетворительные результаты для сцементированных слабоглинистых пород (Сгл<5-10%) с межзерновой пористостью более 20% при насыщении пор водой и эффективном давлении ≥40МПа. Если же эти условия не соблюдаются, то необходим учёт влияния названных факторов на изменяемые величины скорости (или интервального времени).
|
|
|
Для учёта термобарических условий в зависимости от степени консолидации пород водят поправку за уплотнение различными способами.
Широкополосный акустический метод. В аппаратуре широкополосного акустического метода предусмотрено получение интервальных времен, амплитуд и коэффициентов затухания продольных волн, амплитуд и коэффициентов затухания поперечных волн, а также фазокорреляционных диаграмм и волновых картин.
Современная модификация широкополосного акустического метода имеет следующие особенности.
1. В изучаемом участке разреза для любой его точки полностью фиксируется волновая картина, характеризующая поле волн: продольной (Р), поперечной(S), и Лэмба- Стоунли (трубной волны, L-St)
2. Созданные к настоящему времени программы позволяют при обработке информации получить:
- кривые изменения по разрезу интервального времени первых вступлений волн продольной Δτp поперечной Δτs Лэмба-Стоунли ΔτLs-t, а так же их средних амплитуд АР, As, Аь-st и коэффициентов поглощения αр, αs, αL-St
- ФКД
3. Исследование разреза с получением указанной информации проводится при необходимости при различной частоте колебаний, возбуждаемых источником от З КГц до 25 КГц и более, - что позволяет проводить частичное акустическое зондирование, увеличивая радиус исследования скважинным акустическим прибором при уменьшении частоты. Последнее дает возможность изучать разрезы обсаженных скважин в условиях, расформированной зоны проникновения в коллекторах, что в свою очередь, позволяет использовать акустический метод как средство для оценки характера насыщения коллектора в процессе разработки месторождения в эксплуатационных скважинах, а так же в обсаженных разведочных скважинах, бурящихся на стадии доразведки месторождения (выявление пропущенных ранее продуктивных объектов). Весьма перспективным является проведение повторных исследований АКШ до и после перфорации колонны, а так же после обработки призабойной зоны с целью интенсификации притока.
|
|
|
Выделение коллекторов со сложной структурой порового пространства. По данным АКШ для выделения в разрезе трещинных, трещинно-кавернозных коллекторов с плотной непроницаемой матрицей используются следующие признаки.
характерный для данного типа коллекторов «звуковой образ», главными особенностями которого являются:
- резкое уменьшение толщины, иногда вплоть исчезновения изображения, линии на ФКД при одновременном увеличении значений τ всех фаз волн (продольных, поперечных, Лэмба-Стоунли); иногда появление характерной сетки, вызванное явлениями интерференции и дифракции волн;
- заметный рост значений αр, αs, αL-St
- увеличение значений интервальных времен первых вступлении всех видов волн;
2. увеличение коэффициента сжимаемости породы βо, рассчитываемого на основе зарегистрированных значений Δτр и Δτs.
Данные АКШ позволяют рассчитать величину коэффициента Пуассона υ и модуль Юнга Е по формулам:
 2.8
2.8 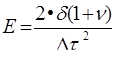 2.9
2.9
В этом состоит преимущество АКШ по сравнению со стандартным АК, поскольку при расчете величины β по данным АК приходится задаваться вероятными для изучаемого объекта значениями υ и E.
Далее рассчитывается βо по одной из следующих формул:
 2.10
2.10
 2.11
2.11
Определение нефтенасыщенности пород. Новый способ определения насыщения пород по данным АКШ основан на использовании кинематических параметров продольной и поперечной волн в комплексе со стандартными методами ГИС. Физической основой способа является различие сжимаемостей водо-, нефте-, и газонасыщенных пород.
Если сравнивать распределение удельных сопротивлений и изотермических сжимаемостей среди наиболее распространенных минералов и насыщающих флюидов продуктивных коллекторов, то аномальным компонентом в ряду удельных сопротивлений
будет пластовая вода (пониженные значения). Она очень широко дифференцирует породы-коллекторы по характеру насыщения. Трудности обычно возникают при учете влияния минерализации пластовой воды и содержания битума, структуры порового пространства по и содержания битума, структуры порового пространства, глинистости и характера смачиваемости коллектора. В случае сравнения изотермических сжимаемостей, аномально упругим свойством среди компонент нефтяного пласта является сжимаемость подвижной нефти. Битум и вода близки по сжимаемости. Битум, не имеющий, как правило, существенного газового фактора будет отмечаться, как дополнительное водородосодержание. Значительно меньше на результаты влияет минерализация пластовой воды, фактор смачивания, структура порового пространства.
|
|
|
Однако аномально высокой сжимаемостью обладает нефтяной газ в свободной фазе, появляющийся при снижении давления нефти ниже давления насыщения. При наличии нефтяного газа в свободной фазе даже при малом газосодержании существенно изменяются упругие свойства пласта, что легко можно установить качественно по волновой картине, однако в этом случае становится невозможным количественное определение нефтенасыщенности такого пласта по его упругим свойствам.
Однако, несмотря на кажущуюся простоту решения проблемы определения нефтенасыщения пластов, не содержащих свободной газовой формы, высокие требования предъявляются к определению коэффициентов сжимаемости породы в целом, минералов, нефти и газа.
Применяя уравнения 2.8, 2.9 к горной породе, допуская в ней только упругие деформации, можно вычислить сжимаемость породы β, решая уравнение 2.10, 2.11 при условии, что величины υ, E, δ известны из данных эксперимента или обобщенных сведений для различных классов горных пород. В дальнейшем основным объектом исследований при интерпретации данных АКШ становится параметр β, который, является источником информации о емкостных свойствах породы и составе флюидов, насыщающих породу.
Известно полученное теоретическим путем для модели породы, составляющие, которой ведут себя как идеально упругие однородные и изотропные среды, уравнение Ф.Гассмана:
 2.12
2.12
где βо, βcк, βтв,βж соответственно сжимаемости породы, скелета породы, твердой фазы и жидкости (флюида), заполняющие его поры.
Модель Ф.Гассмана не учитывает упругой связи между твердой и флюидальной компонентами, которая присутствует в реальных породах. Для преодоления этого недостатка В.М. Добрынин предложил уравнение:
 2.13
2.13
где μр- коэффициент, учитывающий влияние включений, присутствующих в реальных породах, на упругие характеристики породы.
Коэффициент упругой связи αсв твердой и флюидальной фаз породы определяется выражением:
 , 2.14
, 2.14
где βп - коэффициент сжимаемости пор.
На основании изложенного, получено уравнение для коэффициента объемной сжимаемости породы βо при динамических нагрузках (динамическая сжимаемость):
 2.15
2.15
для газонасыщенных терригенньгх коллекторов сжимаемость породы значительно
меньше сжимаемости флюида, поэтому  , αсв=1, поэтому уравнение 2.15
, αсв=1, поэтому уравнение 2.15
принимает вид:
 2.16
2.16
Для количественной интерпретации используется набор комплексных, параметров зависимость комплексного безразмерного параметра, названного «индексом динамической сжимаемости» (ИДС), от коэффициента водонасыщения пласта. ИДС характеризует соотношение сжимаемостей минералов, пор породы, нефти, газа и воды. Для его определения необходимо знать скорости (интервальные времена) продольных и поперечных волн, пористость и плотность изучаемых отложений.
Основой для расчета кривых служат широко известные теории деформации пористых тел М.Био и Ф.Гассмана, модифицированные В.М.Добрыниным применительно к определению нефтенасыщенности коллекторов. При этом были учтены важнейшие ограничения в применении этих теорий для практических целей.
Получены два семейства кривых для нефтегазонасыщенных пластов: кривые с параметром нефтенасыщенности, изменяющимся к пределах kн= 0-0,8 и кривые с параметром газонасыщенности - kг = 0-0,5.
Одна из кривых получена для условий нефтеводонасыщенного пласта без свободной газовой фазы (kг = 0). Он имеет плавный характер и диапазон изменения ИДС достигает 70% при изменении коэффициента водонасыщения от предельной величины kв=kв.о до kв= 100%.
При наличии в порах небольшого количества свободного газа (kг = 0,02 -0,05) кривые для определения kврезко выполаживаются, т.к резко снижается дифференциация пласта по нефтенасыщению. Это делает затруднительным количественные определения нефтенасыщенности. При kг= 0,5 все семейства кривых ИДС = f (kв)устремляется к предельному значению, соответствующему отсутствию упругой связи между флюидом и твердой фазой породы. В этих случаях ИДС может лишь служить очень чувствительным индикатором присутствия свободного газа в нефтенасыщенном пласте.
Специальная часть
Информативность метода ВИКИЗ при изучении песчано-глинистых разрезов
|
|
|


