 |
Основные понятия и определения теории игр
|
|
|
|
Методические указания
к контрольной работе №1 по дисциплине
“Теория игр и исследование операций ”
Новочеркасск
ЮРГТУ (НПИ)
УДК 519.24 (076.5)
Рецензент канд. техн. наук, доц. В.Ф. Петров
Гузыкина Т.Н.
Матричные игры: Метод. указания к контрольной работе № 1 по дисциплине “Теория игр и исследование операций” / Юж.-Рос. гос. техн. ун-т (НПИ). Новочеркасск: ЮРГТУ (НПИ), 2003. 32 с.
Указания содержат теоретический материал, примеры решения типовых задач, варианты заданий по дисциплине “Теория игр и исследование операций”.
Предназначены для студентов специальности 03210.00 - “Математика с дополнительной специальностью информатика” заочной формы обучения.
ã Южно-Российский государственный
технический университет, 2003
ã Гузыкина Т.Н., 2003
ОГЛАВЛЕНИЕ
| 1. Требования к содержанию и оформлению контрольной работы…………………………………..…………………….. 2. Основные понятия и определения теории игр…………… 3. Матричные игры…………………………………………….. 3.1. Принцип максимина; решение игры в чистых стратегиях 3.2. Решение матричной игры в смешанных стратегиях……. 3.2.1 Решение игры 2´2…………………………………… 3.3. Графоаналитический метод решения матричных игр….. 3.3.1 Решение игры 2´n…………………………………... 3.3.2 Решение игры m´2………………………………….. 3.4. Сведение матричной игры к задаче линейного программирования ……………………………………….………... 3.5. Доминирование стратегий ……………………..………… 3.6. Варианты контрольной работы…………………………... Библиографический список…………………………………… |
1. ТРЕБОВАНИЯ К СОДЕРЖАНИЮ И ОФОРМЛЕНИЮ
КОНТРОЛЬНОЙ РАБОТЫ 
|
|
|
Контрольная работа состоит из семи задач. Вариант задания выбирается студентом самостоятельно так, что последняя цифра номер зачетной книжки студента соответствует индексу платежной матрицы в задачах 1-7. Результатом решения матричной игры являются вектора оптимальных стратегий и цена игры; для задачи 1 указываются верхняя и нижняя чистая цена игры, максиминная и минимаксная стратегии, седловая точка. Алгоритм решения игры 2´2 предполагает, что обе стратегии игроков активные, поэтому прежде чем решать задачу 2 в смешанных стратегиях следует убедиться, что решение в чистых стратегиях отсутствует. Применение свойства доминирования для сокращения размерности матрицы допускается только в задаче 6. В задачах 3, 4 поле рисунка по горизонтальной оси определяется отрезком [0,1]; на рисунках указываются: оптимальные вероятности принятия игроками своих первых стратегий, цена игры. В задаче 6 приводятся задачи линейного программирования (ЗЛП) для обоих игроков; решение игры находится по ЗЛП для игрока А или для игрока В с использованием двойственных оценок.
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ИГР
Определение 1. Теория игр – теория математических моделей принятия оптимальных решений в условиях конфликта интересов участников игры и неопределенности внешних условий.
Определение 2. Конфликтная ситуация – ситуация в практической деятельности людей, когда два или несколько участников, имея различные цели и средства их достижения, пытаются достичь результата в условиях, когда никто из них полностью не влияет на ход событий.
Замечание 1. Участник конфликта принимает решения не на основании объективных обстоятельств, а на основании своих субъективных представлений о них, т.е. имеет место неполное представление об обстановке к моменту принятия решения.
Замечание 2. Участник конфликта располагает только набором вариантов обстоятельств, в которых следует принимать решения. При этом ему не известны ни вероятностные характеристики факторов, влияющих на обстоятельства, ни их вероятностное распределение на множестве вариантов; таким образом, он действует в условиях неопределенности.
|
|
|
Определение 3. Игровая модель – формальная модель принятия решений в условиях неопределенности, когда у принимающего решения субъекта имеется некоторый противник, уточняющий неизвестные варианты таким образом, чтобы поставить субъекта в наихудшее положение.
Определение 4. Понятие оптимальности в теории игр (ТИ) интерпретируется как объективная разумность, выгодность, целесообразность, справедливость, осуществимость, устойчивость.
Выбор принципа оптимальности производится в соответствии с конкретной постановкой задачи, формализуемой игровой моделью; принцип оптимальности должен быть реализуем.
Предметом формального моделирования ТИ являются разумные действия лиц и коллективов, объединенных по какому-либо признаку, имеющих различные интересы и преследующих различные цели в условиях конфликта и неопределенности.
Определение 5. Совокупность правил и условий, оговоренных игроками, называется игрой, каждая их конкретная реализация – партией.
Определение 6. Сумма, которую получает каждый игрок в результате игры, называется выигрышем;в случае, если выигрыш отрицательный, он интерпретируется как проигрыш.
Определение 7. Набор правил, однозначно определяющих действия игрока во всех возможных случаях развития игры называется стратегией.
Определение 8. Принятие игроком в процессе игры того или иного решения и его реализация называется ходом; если ход выбирается случайным образом, то он называется случайным, в противном случае – личным.
Определение 9. Формализованное правило, согласно которому можно определить выигрыш каждого игрока в конкретной ситуации, т.е. в зависимости от стратегий, выбранных игроками, называется платежной функцией игры.
Основные признаки, по которым производится классификация игр, следующие: количество игроков, количество стратегий, характер взаимоотношений, характер выигрышей, вид функции выигрыша, количество ходов, состояние информации.
|
|
|
Определение 10. Игра, в которой принимают участие два игрока(n =2) называется парной, при n >2 – множественной (игры одного игрока в ТИ не рассматриваются).
Определение 11. Если в игре каждый из игроков имеет конечное число стратегий, то игра – конечная, если хотя бы один из игроков имеет бесконечное число стратегий – бесконечная.
Определение 12. Игры, в которых игроки не могут вступать в коалиции, называются бескоалиционными, в противном случае – коалиционными; если коалиции определены априори, игра называется кооперативной.
Определение 13. Если сумма выигрышей всех игроков в каждой партии игры равна нулю, то такая игра называется игрой с нулевой суммой. Частный случай при n =2: парная игра с нулевой сумой называется антагонистической, т.к. выигрыш А равен проигрышу В.
Определение 14. Конечная парная игра с нулевой суммой называется матричной игрой; функция выигрыша первого игрока задается в виде матрицы, у которой строки – стратегии первого игрока, столбцы – стратегии второго. Такая матрица называется платежной матрицей игры.
Определение 15. Конечная игра двух игроков с ненулевой суммой называется биматричной; функции выигрышей задаются для обоих игроков в виде их платежных матриц.
Выделяются и другие классы игр по виду функции выигрыша.
Определение 16. Игры, оканчивающиеся после одного хода – одношаговые, иначе – многошаговые.
Определение 17. Если игроку известны все предыдущие ходы, то игра называется с полной информацией; иначе – с неполной.
Перечисленные виды игр и приведенные признаки их классификации не являются полными; существуют и другие виды игр и системы их классификации.
МАТРИЧНЫЕ ИГРЫ
3.1. Принцип максимина; решение игры в чистых стратегиях
Теория игр обосновывает выбор принципов оптимальности поведения игроков и разрабатывает алгоритмы нахождения оптимальных стратегий и выигрышей игроков. Признаками игровой ситуации являются: наличие конфликта интересов, неполнота и неопределенность информации. Такие условия вынуждают участника игры действовать по логике расчета на наихудшую реализацию неизвестных условий, выбирая из наихудших реализаций лучшую. В качестве принципа оптимальности поведения игроков в матричных играх, выработанного теорией игр, служит принцип устойчивости, когда отклонение от оптимального поведения невыгодно ни одному игроку при условии, что другой действует оптимальным образом.
|
|
|
По определению (14) платежная функция матричной игры задается в виде матрицы 
, элемент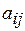 
которой есть выигрыш первого игрока при условии, что первый игрок (игрок А) выбрал стратегию i из набора возможных стратегий Аi, 
, а второй игрок (игрок В) выбрал стратегию j из набора возможных стратегий Вj, 
:
| j i | В1 ... | Вj | ...Вn | ||
| А= | А1 . . . | ||||
| Аi | aij | ||||
| . . . Ат | |||||
Пример 1. Рассмотрим следующую игровую ситуацию: два игрока выбрасывают 1, 2, 3, 4, 5 пальцев руки.Если сумма нечётная, первый игрок выигрывает сумму очков, равную количеству пальцев, выброшенных обоими игроками; если сумма чётная – второй выигрывает такую же сумму очков.
Решение
Количество стратегий игроков n = m = 5.
Запишем стратегии игроков:
Ai = {игрок А выбросил i пальцев}, 
,
Bj = {игрок B выбросил j пальцев}, 
.
Платежная матрица игры имеет следующий вид:
 j
i
| В1 | В 2 | В 3 | В 4 | В 5 |
| А1 | -2 | -4 | -6 | ||
| А 2 | -4 | -6 | |||
| А 3 | -4 | -6 | -8 | ||
| А 4 | -6 | -8 | |||
| А 5 | -6 | -8 | -10 |
Опишем логику поведения игроков, учитывая антагонизм интересов игроков, вынуждающий каждого из них рассчитывать на сильное противодействие другого. Первый игрок старается максимизировать свой выигрыш в условиях неопределённости, создаваемой антагонистическими действиями второго игрока. В этом случае игрок А для каждой своей стратегии i определяет свой гарантированный выигрыш, т.е. выигрыш в худшей для себя ситуации
.
Т.к. выбор любой стратегии в его распоряжении, чтобы максимизировать свой гарантированный выигрыш игрок А из гарантированных выигрышей по стратегиям выбирает максимальный:
(1)
Определение 18. Величина 
, вычисленная по (1), называется нижней чистой ценой игры и интерпретируется как максимальный гарантированный выигрыш А; стратегия 
, при которой выполняется (1), называется максиминной стратегией.
Определим нижнюю чистую цену игры и максиминные стратегии для примера 1:
максиминные стратегии - А1, А2.
Второй игрок старается минимизировать свой проигрыш в условиях противодействия игрока А. Поэтому игрок В для каждой своей стратегии j определяет свой гарантированный проигрыш, т.е. то, что он вынужден будет заплатить при самом неблагоприятном поведении А:
|
|
|
.
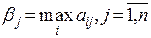Т.к. он волен выбирать любую свою стратегию, он, естественно, выбирает ту, что минимизирует его проигрыш:
. (2)
Определение 19. Величина β, рассчитанная по (2), называется верхней чистой ценой игры и интерпретируется как минимальный гарантированный проигрыш В;cтратегия 
, при которой выполняется (2), называется минимаксной стратегией.
Определим верхнюю чистую цену игры и минимаксные стратегии для примера 1:
минимаксная стратегия - В1.
Определение 20. Решением игры называется процесс нахождения оптимальных стратегий игроков и цены игры и ценой матричной игры называется выигрыш игрока А (или проигрыш В).
Определение 21. Если для чистых максиминной и минимаксной стратегий выполняется равенство α = β при и , то:
- стратегии и называются уравновешивающей парой и являются оптимальными стратегиями;
- точка (iо, jо) называется седловой точкой;
- элемент 
называется седловым элементом и является ценой игры.
Пусть игроки А и В в матричной игре с платёжной матрицей могут выбирать одну из стратегий совокупности {Ai} или {Bj}. Пусть pi, qj вероятности того, что игрок А выберет Ai, а игрок В - Bj. Тогда, учитывая, что набор стратегий представляет собой полную группу событий, имеют место условия нормировки: 
Образуем векторы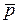 
и 
следующим образом: если А выбрал стратегию Ai, то 
;если В выбрал стратегию Bj, то 
.
Определение 22. Вектора 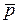и , описывающие выбор стратегий игроками А и В, называются стратегиями игроков; чистая стратегия Ai или Bj – это стратегия, выбранная с вероятностью, равной единице.
Определение 23. Формализованное правило, согласно которому можно определить выигрыш каждого игрока в конкретной ситуации, т.е. в зависимости от стратегии, выбранной данным игроком и остальными участниками игры, называется платежной функцией игры.
Определим платёжную функцию матричной игры по схеме:
1. Введем случайные величины ξ, η такие, что
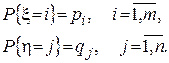(3)
Здесь Р{с} – вероятность того, что событие с произошло.
Соотношения (3) по определению задают законы распределения случайных величин ξ и η.
2. Образуем систему случайных величин ξ и η - (ξ, η) или вектор, компонентами которого являются значения случайных величин ξ и η.
3. Введем функцию системы случайных величин ν такую, что она принимает значение элемента платежной матрицы, если случайная величина ξ=i и случайная величина η=j:
.
Таким образом, значение случайной функции ν есть величина выигрыша игрока А (проигрыша игрока В) при различных стратегиях игроков.
4. Найдем средний выигрыш игрока А как математическое ожидание функции двух случайных аргументов:
. (4)
Здесь М[n] - математическое ожидание случайной функции n.
Игроки А и В выбирают стратегии тайно и независимо друг от друга, следовательно, случайные величины ξ и η независимы, поэтому можно записать:
.
Тогда (4) запишется в виде
.
Определение 24. Функция вида 
называется платёжной функцией матричной игры.
Определение 25. Стратегии 
и 
называются оптимальными, если для каждой стратегии игроков – 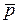, выполняется условие
. (5)
Условие (5) означает, что при каждой неоптимальной стратегии игрока
А 
его выигрыш не возрастает в сравнении с оптимальным при условии, что игрок В действует оптимальным образом, а при каждой неоптимальной стратегии игрока В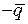 
его проигрыш не убывает в сравнении с оптимальным.
Примем без доказательства теорему, показывающую связь седловой точки с ценой игры и оптимальными стратегиями.
Теорема 1. Для того чтобы точка (i0, j0) была седловой, необходимо и достаточно, чтобы чистые стратегии 
и 
или 
, 
были оптимальными; при этом цена игры 
.
Следствие из теоремы 1: если платёжная матрица А имеет седловую точку, то обязательно существуют оптимальные чистые стратегии; если седловой точки нет, то оптимальные стратегии могут быть только смешанными.
3.2. Решение матричной игры в смешанных стратегиях
Определение 26. Стратегии 
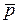и называются смешанными, если хотя бы два значения вероятностей выбора стратегий первым и (или) вторым игроком не равны нулю:
Исходя из того, что стратегии представляют собой полную группу событий, выполняется условие нормировки: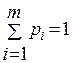 
; 
.
Примем без доказательства следующую теорему.
Теорема 2. Для того чтобы смешанные стратегии игроков были оптимальными, необходимо и достаточно выполнение условий:
;
.
Т.е. выигрыш игрока А при его оптимальной стратегии 
и любой чистой стратегии игрока В не меньше цены игры, а проигрыш игрока В при его оптимальной стратегии 
и любой чистой стратегии игрока А не больше цены игры.
Определение 27. Чистые стратегии называются активными, если в оптимальной смешанной стратегии их вероятности не равны нулю.
Пусть, например, оптимальная стратегия игрока А имеет вид
тогда 
,
, 
являются активными стратегиями игрока А (аналогично для игрока В).
Примем без доказательства следующую теорему.
Теорема 3. Если первый из игроков придерживается своей оптимальной смешанной стратегии, а второй игрок выбирает любую активную стратегию, то выигрыш первого игрока равен цене игры; аналогично для второго игрока:
;
.
Здесь 
и 
- подмножества индексов активных стратегий соответственно игрока В и игрока А.
3.2.1. Решение игры 2 
2
Найдем оптимальную стратегию игрока А. В соответствии с теоремой 3 применение игроком А оптимальной стратегии 
должно обеспечить ему при любых стратегиях игрока В - 
выигрыш, равный цене игры при условии, что В выбирает стратегию из активных:
. (6)
Здесь s – количество активных стратегий игрока В. Рассмотрим игру, в которой m = n =2 с платежной матрицей 
и векторами стратегий 
и 
.
Очевидно, что число активных стратегий игрока B – s = 2. С учетом этого (6) запишется в виде
для 
;
для 
. (7)
Из (7) получим
.
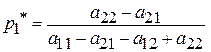Тогда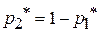 
и оптимальная стратегия игрока А найдена: 
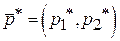. Аналогичным образом находится оптимальная стратегия игрока В. Применение игроком В оптимальной стратегии 
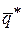должно обеспечить при любых стратегиях игрока А проигрыш, равный цене игры при условии, что А выбирает стратегию из активных:
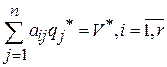. (8)
Здесь r – количество активных стратегий игрока А.
Запишем условие (8) для случая игры 2´2, когда n = r = 2. Будем иметь при 
и 
:
для 
;
для 
. (9)
Из (9) получим
.
Тогда и оптимальная стратегия игрока найдена: 
. Затем, подставив 
в одно из уравнений (9) или 
в одно из уравнений (7), получим цену игры 
.
3.3. Графоаналитический метод решения матричных игр
3.3.1. Решение игры 2 ´ n
Для игры 2´n имеем платежную матрицу вида
.
Количество стратегий игрока А – m = 2 и вектор стратегий имеет вид 
; количество стратегий игрока В –п и вектор стратегий 
. Положим р1=х, тогда р2= 1 -х. Если игрок В выбрал чистую стратегию Вj из набора возможных, то выигрыш игрока А является линейной функцией от х – вероятности принятия им первой стратегии:
Таким образом, каждой стратегии Вj соответствует прямая lj (x), 
. Введём в рассмотрение функцию
.
Не сложно показать, что графиком 
будет нижняя огибающая всех прямых, соответствующих стратегиям игрока В. Другими словами, ломанная есть нижняя граница выигрыша игрока А. Игрок А стремится максимизировать свой выигрыш, поэтому он должен выбирать свою оптимальную стратегию 
так, чтобы аргумент х приносил максимум , т.е. максимум гарантированного выигрыша:
.
Графически х* будет наивысшей точкой ломанной 
, тогда р1*= х* – абсцисса наивысшей точки; ордината наивысшей точки – цена игры, т.к. это значение выигрыша А при 
. Зная цену игры V*, ставим ей в соответствие активные стратегии В. Пусть это будут стратегии номер s и r, соответствующие прямым ls (x) и lr (x) и дающим в пересечении точку с абсциссой х*.
Тогда вектор оптимальных стратегий игрока В имеет вид
= (0 ,…ps, 0 …pr, 0…0). Значения qs и qr находятся для матрицы А ' вида
А '= 
по правилу игры 2´2:
;
.
Графическая иллюстрация рассуждений приведена на рис. 1.
Рис.1
Пример 2. Для игры с платежной матрицей
найти решение графоаналитическим методом.
Решение
1. Запишем lj (x) = a1j · x + a2j ·(1 -x), 
:
l1 (x) = 1· x - 1· (1 -x) = 2· x- 1,
l2 (x) = 4· x - 2 · (1 -x) = 6· x- 2,
l3 (x) = 0· x + 1· (1 -x) = -x+ 1,
l4 (x) = -1· x + 5· (1 -x) = -6· x+ 5.
2. 
Построим графики lj (x), 
; найдем нижнюю огибающую, её Верхнюю точку, активные стратегии игрока В.
верхняя точка нижней огибающей x * есть точка пересечения 
и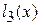 
(см рис. 2), поэтому активными стратегиями игрока В являются В1 и В2, т.е. s = 1, r = 3.
3. Найдём численное значение вероятности принятия игроком А первой стратегии, т.е. точку пересечения l3 (x) и l4 (x)из условия
2 x* -1 = -x* + 1, x* = 2/3,тогда = (2/3, 1/3).
4. Найдём цену игры V* = l3 (x*) = l4 (x*) = 2 · 2/3 – 1 = 1/3.
5. По активным стратегиям игрока В для платёжной матрицы А '= 
определим 
и 
:
;
.
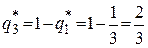= (1/3, 0, 2/3, 0).
Ответ: = (2/3; 1/3); = (1/3, 0, 2/3, 0); V* = 1/3.
Выделим по виду j (x) частные случаи.
Случай 1. Рассмотрим случай, когда 
имеет множество точек, максимальных на [0; 1]. Тогда игрок А имеет бесконечное множество оптимальных страте-гий, 
= (x*, 1 -x*), где x* из отрезка [ a, b ] (см. рис. 3). Оптимальной стратегией игрока В является чистая стратегия Вк:
= (0,…0, 
, 0,…,0).
Цена игры j (x*) = V (
) одна и та же для всех x* Î[ a, b ].
Случай 2: Если 
достигается в крайних точках отрезка [0,1]
а) если 
в точке
х* =0, то оптимальной стратегией игрока А будет чистая стратегия = (0;1), а оптимальной стратегией игрока В - = (0,…0, , 0,…0), где номер k такой, что точка (х*,j (x)) лежит на прямой lk (x); цена игры j (x*) = lk (x);
б) если 
достигается в точке х* = 1 (см. рис. 5), то оптимальной стратегией игрока А будет чистая стратегия = (1, 0), оптимальной стратегии игрока В – чистая стратегия = (0,…0,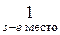 
,…0), где s такое, что (х*, j (x)) лежит на ls (x); цена игры j (x*) = ls (x*).
3.3.2 Решение игры m´2
Для игры m´2 платёжная матрица имеет вид
;
вектора стратегий: игрока А = 
, …, 
; игрока В = 
, 
.
Положим q1= y, q2 = 1-y, тогда если игрок А выбрал чистую стратегию Аi, то проигрыш игрока В является линейной функцией у; для фиксированного i имеем
. (10)
Таким образом, каждой стратегии игрока А - Аi, соответствует прямая hi 
.
Введём в рассмотрение функцию Y(у) вида Y(у) = 
, легко показать, что ломаная Y(у) есть верхняя огибающая всех прямых, соответствующих чистым стратегиям игрока А. Другими словами, ломаная есть верхняя граница проигрыша игрока В.
Игрок В стремится минимизировать свой проигрыш, поэтому он должен выбирать свою оптимальную стратегию так, чтобы аргумент - у приносил минимум 
, т.е. минимум гарантированного проигрыша:
.
Графически у* будет наинизшая точка ломаной , тогда q1* = y*, q2* = 1 -y*, где y – абсцисса наинизшей точки; ордината точки – цена игры, т.к. это – значение проигрыша игрока В при стратегии .Зная цену игры V*, ставим в соответствие ей оптимальные стратегии игрока А. Пусть активными будут стратегии Аs и Ar. Тогда = (0,…, ps,0, …, pr,0,…,0), где s и r – номера активных стратегий игрока А, т.е. номера прямых hs (y) и hr (y), дающих в пересечении точку с абсциссой у*. Значения ps и pr находятся для матрицы вида А'= 
по правилу игры 2´2:
; 
(11)
Графическая иллюстрация рассуждений приведена на рис.6.
Решение игры m´2 аналогично решению игры 2´n:
1) 
;
2) точка у* есть точка пересечения стратегий s и r; значения у* находятся из соотношения 
, тогда 
3) активные стратегии игрока А - Аs и Аr; по формулам (11) находим ps*, pr* и 
.
Аналогично предыдущему рассматриваются частные случаи.
Случай 1. Точек минимума на [ a,b ] – множество (рис. 7), тогда для игрока В имеет множество решений 
, где у * из отрезка[ a,b ]; оптимальная стратегия игрока А - 
* = (0,…,0, 
, 0,…,0); цена игры V*=V ( *, 
*).
Случай 2. Минимум достигается в крайних точках отрезка [0,1] (см. рис. 8, 9):
a) 
,
= (0,…,0, 
,0,…,0), V*=V ( *, *);
б) 
, * = (0,…,0, 
, 0,…,0), V*=V ( *, *).
Пример 3. Для игры с платёжной матрицей
найти решение графоаналитическим способом.
Решение
1. Запишем hi (у) = ai 1· у + ai 2· (1 -у), 
:
h 1(у) = 4· у + 3· (1- у) = у + 3,
h 2(у) = 2· у + 4· (1- у) = -2· у+ 4,
h 3(у) = 0· у + 5· (1- у)= -5· у+ 5,
h 4(у) = -1· у + 6· (1- у) = -7· у+ 6.
2. Построим график hi (у), ; найдём верхнюю огибающую, её нижнюю точку, активные стратегии игрока А (см. рис. 10).
Нижняя точка верхней огибающей у* есть точка пересечения hi (у) = hi (у), поэтому активными стратегиями игрока А являются А 1 и А 4, т.е. s =1, r =4.
3. Найдем из соотношения h 1(у*) = h 4(у*)или у*+ 3 = -7 у* + 6: у* = 3/8; = (3/8, 5/8).
4. Найдем цену игры
V* = h 1(у*) = h 4(у*) = 
.
5. По активным стратегиям игрока А для платежной матрицы А'= 
определим 
и 
: 
;
; 
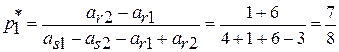= (7/8, 0, 0, 1/8).
Ответ:
