Главная | Обратная связь | Поможем написать вашу работу!

Сведение матричной игры к задаче линейного программирования

Примем без доказательства следующую теорему:

Теорема 4. Смешанные стратегии игроков 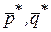в игре с платежной матрицей А и ценой игры V^* будут оптимальны и в матричной игре с 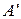, элементы которой есть линейная комбинация элементов А:

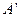= { a_ij } = {ba_ij +c}, 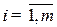, 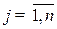; b,c =const, b>0,

при этом цена игры 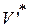= bV^* + c.

Рассмотрим процедуру сведения матричной игры к задаче линейного программирования (ЗЛП). Запишем условия, которым должны удовлетворять вектора оптимальных стратегий игроков:

по теореме 2 имеем , ,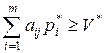

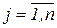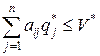
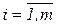, ; (12)

условия нормировки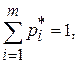

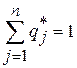; (13)

ограничения на знак , ,

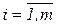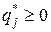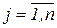, . (14)

По теореме 4 за счет преобразования А в А‘ можно добиться того, чтобы все элементы А' были больше нуля. Не нарушая общности, будем считать, что 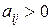, , 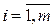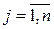. Тогда цена игры будет строго больше нуля: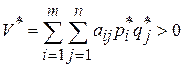

Разделим обе части (12) и (13) на V^* (мы можем это сделать, т.к. V^* >0) и сделаем замену переменных: 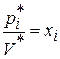, 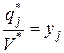. Тогда условия (12)-(14) запишутся следующим образом:

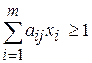
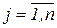, ; (15)

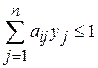
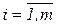, ; (16)

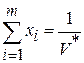; (17)

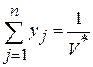; (18)

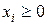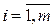, ;(19)

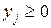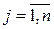, . (20)

Из полученных условий сформулируем ЗЛП для игрока А. Игрок А стремится максимизировать свой выигрыш V^*, поэтому для него , тогда из (17) получим выражение для функции цели:

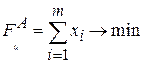. (21)

Запишем ограничения на область, в которой находится минимум функции цели:

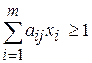
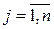, ; (22)

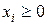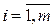, .(23)

Аналогично игрок В стремится минимизировать свой проигрыш V^*, поэтому для него 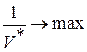и ЗЛП для игрока В имеет следующий вид:

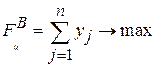; (24)

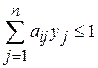
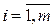; (25)

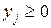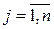, . (26)

Решив полученные задачи линейного программирования и сделав переход от x_i к 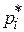и от y_j к 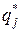, получим решение игры.

Схема перехода от решения ЗЛП к решению игры:

- определяем цену игры 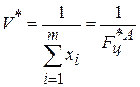или ;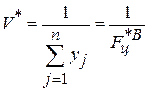

- определим компоненты векторов оптимальных стратегий игроков , ; , .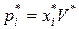

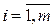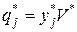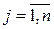Замечание 1. ЗЛП (21) –(23) и (24) – (26) – двойственные, поэтому, решив прямую задачу по последней симплекс-таблице, в столбцах замещения для дополнительных переменных можно найти решение двойственной задачи; этот прием позволяет существенно сократить объем вычислений.

Замечание 2. Если матрица А преобразовывалась в 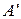, то следует перейти от 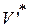к V^*, для этого используется обратное преобразование : .

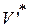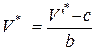Пример 4. Решить игру сведением к ЗЛП; платежная матрица имеет вид .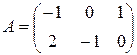

Решение

1. Проверим, существует ли решение игры в чистых стратегиях:

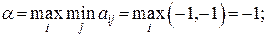
максиминные стратегии А₁, А₂;

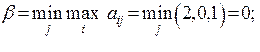
минимаксная стратегия В ₂;

-нижняя чистая цена игры не равна верхней чистой цене игры, α ≠ β, значит, седловой точки нет и решения в чистых стратегиях нет.

2. Проверим, возможно ли уменьшение размерности задачи за счет использования свойства доминирования стратегий:

- среди стратегий игрока А доминирования нет;

- стратегия В ₃доминируется стратегией В ₂, поэтому матрица А преобразуется к виду

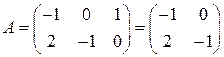
и вектора стратегий игроков будут иметь вид = , ; = , .

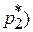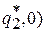3. Для того чтобы решить игру сведением к ЗЛП, необходимо выполнение условия V^*>0. Это достигается сведением платежной матрицы А к матрице 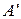, у которой 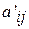> 0, 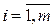, 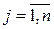. Пусть b =1, с=2, тогда 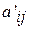= 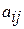+ 2

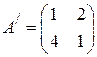4. Запишем ЗЛП для игрока В:

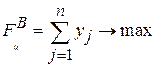; или F_ц^B = y ₁ +y ₂ ® max;

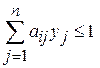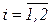, ; y ₁ + 2 y ₂ £ 1;

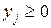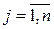, ; 4 y ₁ +y ₂ £ 1;

y ₁, y ₂ ³ 0.

5. Вводим дополнительные неизвестные, сводя общую ЗЛП к каноническому виду:

F_ц = y ₁ +y ₂ ® max;

y ₁ +2y ₂ +y ₃ = 1;

4 y ₁ +y ₂ + y ₄= 1;

, .

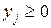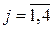6. Решаем задачу симплекс-методом:

	Основные переменные	Дополнительные переменные
F_ц
e^б	у^б	b_i	у ₁	у ₂	у ₃	у ₄
	у ₃
	у ₄
Z		-1	-1
	у ₃	3/4		7/4		-1/4
	у ₁	1/4		1/4		1/4
Z	1/4		-3/4		1/4
	у ₂	3/7			4/7	1/7
	у ₁	1/7			-1/7	2/7
Z	4/7			3/7	1/7

7. Из последней симплекс-таблицы имеем: оптимальное значение функции цели ыавыавыы 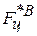=4/7; решение прямой ЗЛП – x ₁=3/7, x ₂=1/7; решение обратной ЗЛП – y ₁=1/7, y ₂=3/7.

8. Найдем решение игры с платежной матрицей :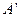

- определим цену игры ;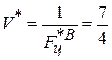

- определим вектора оптимальных стратегий игроков

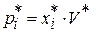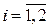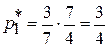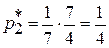, ; ; , тогда ;

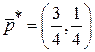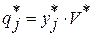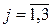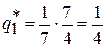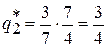, ; ; , тогда; =

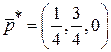9) Найдем решение игры с платежной матрицей А. В соответствии с теоремой 4 вектора остаются такими же, как для игры с платежной матрицей 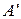, а цена игры находится по формуле

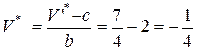Пример 5. Проверить, удовлетворяются ли условия теорем 2 и 3 для полученного решения игры.

По теореме 2 для игрока А имеем условия:

, .

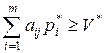
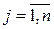Пусть игрок В принял первую чистую стратегию, j =1, тогда получим

;

пусть игрок В принял вторую чистую стратегию, j =2, тогда получим

;

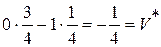пусть игрок В принял третью чистую стратегию, j =3, тогда получим

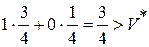Таким образом, условия теоремы 2 выполняются. Аналогично проверяется выполнение теоремы 2 для игрока В.

По условиям теоремы 3 для активных стратегий в условиях теоремы 2 имеем равенства, и действительно у игрока В активными являются стратегии В ₁ и В ₂, j = 1,2, для которых условия теоремы 2 выполняются на равенстве. Таким образом, условия теоремы 3 выполняются.

Доминирование стратегий

Для уменьшения размерности платёжной матрицы используется прием сведения игры с платёжной матрицей А к игре с платёжной матрицей А ', у которой стратегии, вероятности принятия которых равны 0, опущены.

Определение 29. Стратегия игрока А - А_l доминирует его стратегию А_k или А_kдоминируется А_l, если для любой чистой стратегии игрока В выполняется условие

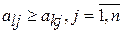; если условие выполняется на строгом равенстве, то стратегии А_l и А_к называются дублирующими.

Определение 30. Стратегия игрока В - В_s доминирует его стратегию В_r или В_rдоминируется В_s, если для любой чистой стратегии игрока А выполняется условие

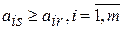; если условие выполняется на строгом равенстве, то стратегии В_r и В_s называются дублирующими.

Примем без доказательства правило:

- при решении матричных игр доминируемые стратегии опускаются и соответствующие компоненты в векторе 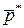или полагаются равными нулю;

- опускаются все дублирующие стратегии, кроме одной, и соответствующие компоненты в 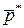и полагаются равными нулю.

Определение 31. Если условие доминирования выполняется на строгом равенстве, то имеет место строгое доминирование.

Примем без доказательства следующие теоремы:

Теорема 5. Если в матричной игре стратегия l доминирует стратегию k и стратегия k оптимальна, то стратегия l тоже оптимальна.

Здесь речь идёт об альтернативных решениях и,опустив доминируемую стратегию, мы можем потерять альтернативное решение игры.

Теорема 6. Если в матричной игре стратегия l строго доминирует стратегию k, то стратегия k не может быть оптимальной.

Таким образом, правило сокращения размерности при строгом доминировании стратегий применяется всегда, при нестрогом - если не нужен весь набор оптимальных решений, включающий альтернативные.

Варианты контрольной работы

Задача 1. Найти решение игры в чистых стратегиях:

; ;

; .

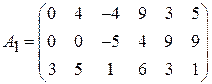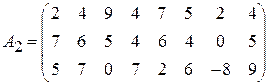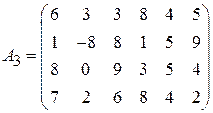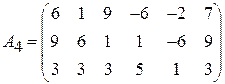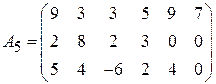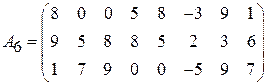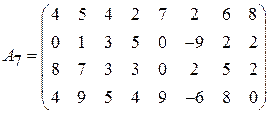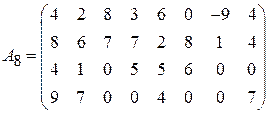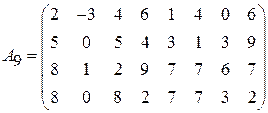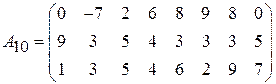Задача 2. Найти решение игры в смешанных стратегиях; игра 2 2:

; ; ; ; ;

; ; ; ; .

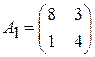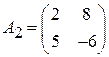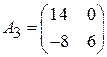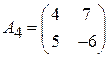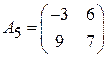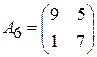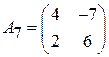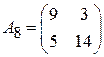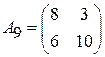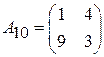Задача 3. Найти решение игры 2 n:

; ;

; .

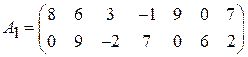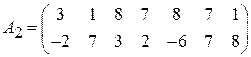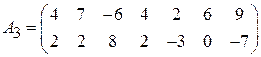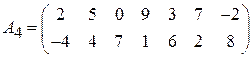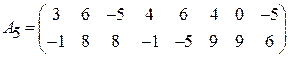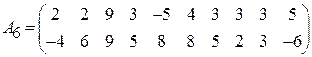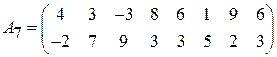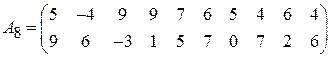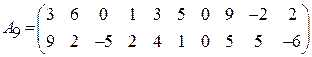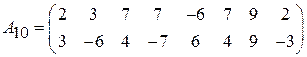Задача 4. Найти решение игры m 2:

; ; ; ;
; ; ;
; ; .

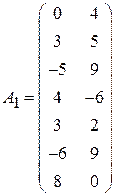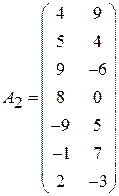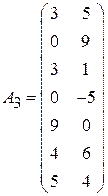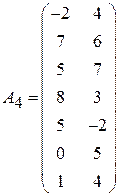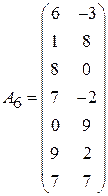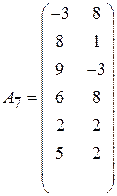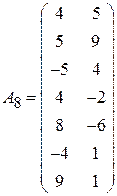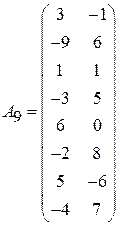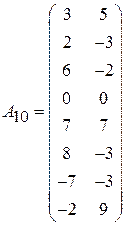Задача 5. Для условий задачи 1 произвести операцию доминирования.

Задача 6. Для условий задачи 3 найти решение игры сведением к ЗЛП: для сокращения размерности задачи использовать свойства доминирования.

Задача 7. Проверить, удовлетворяют ли условия теорем 2 и 3 решению, полученному в задаче 6.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Воробьёв Н.Н. Теория игр для экономистов-кибернетиков. – М.: Наука, 1985.

2. Матричные игры / Под. ред. Н.Н. Воробьева. – М.: Физматгиз, 1961.

3. Карлин С. Математические методы в теории игр, программирование в экономике. – М.: Мир, 1964.

4. Крушевский А.В. Теория игр. – Киев: Вища шк., 1977.

5. Коваленко А.А. Сборник задач по теории игр. – Львов: Вища шк., 1974.

6. Мак-Кинси Д. Введение в теорию игр. – М.: Физматгиз, 1960.

Учебно-методическое издание

Гузыкина Татьяна Николаевна

Матричные игры

Редактор Н.А. Юшко

Подписано в печать 27.05.2003 г. Бумага офсетная. Формат 60´84 1/16. Печать оперативная. Усл.печ.л. 2,79. Уч.-изд.л. 2,86. Тираж 50. Заказ

Южно-Российский государственный технический университет (НПИ) Редакционно-издательский отдел ЮРГТУ (НПИ) Отпечатано в ИД «Политехник» 346428, г. Новочеркасск, ул. Просвещения, 132.

12	Поделиться:

Воспользуйтесь поиском по сайту: