 |
В25. Метод главного критерия.
|
|
|
|
Свертывания векторного критерия в скалярный.
Способы выбора критерия оптимальности.
Используется метод весовых коэффициентов:Вектор w=(w1, …, wn) wi>0 ∑wi=1. Величина wi определяет возможность (вес) i-го критерия оптимальности. Весовые коэффициенты задает эксперт.
Процедуры оценки весовых коэффициентов:
Метод ε-ограничений:1) выбирается одна из целевых функций как основная; 2) остальные записываются в виде ограничений; 3) добавляются свои ограничения.
Позволяет определить количество неухудшаемых решений. Проблемой остается подходящий выбор ε, хотя ограничения ставятся в жесткой форме и более определенно, чем в методе весовых коэффициентов.
В.15 Экстремальные задачи - означает максимум или минимум некоторой функции (наилучшее или оптимальное значение того или иного показателя: наивысшая производительность труда).
Экстремальные задачи классифицируются как: 1) дискретные, 2) комбинаторные; 3) целочисленные; 4) булевы; 5) вещественные; 6) бесконечномерные.
Максимум и минимум — наибольшее и наименьшее значения функции по сравнению с ее значениями в достаточно близких точках. Точки максимума и минимума называются точками экстремума(крайними).
Теорию решения задач на отыскание наибольших и наименьших величин называют теорией экстремальных задач или теорией оптимизации.
Минимакс — правило в теории принятия решений для минимизации возможных потерь. Критерий минимакса первоначально был сформулирован в теории игр для игры двух лиц с нулевой суммой в случаях последовательных и одновременных ходов, впоследствии получил развитие в более сложных играх и при принятии решений в условиях неопределённости. С понятием минимакса связано понятие максимина (значение минимакса не меньше значения соответствующего максимина).
|
|
|
Максимин - выбирается вариант с наилучшим из наихудших исходов; его использование характерно для субъектов, избегающих риска; означает, что нижняя цена игры определяет минимальный выигрыш участника. Минимакс означает, что верхняя цена игры определяет максимальный проигрыш участника
В.16 Раздел математическогопрограммир. В отличие от статических, не зависящих от времени, динамические модели описывают производственные процессы или системы движений в зависимости от временных периодов, учитывая те периоды, которые прошли ранее и произойдут в будущем.Динамические модели позволяют прогнозировать развитие процесса на будущее и соответствующим образом реагировать на определенные изменения.Динамические модели представляют собой многошаговый процесс. Каждый текущий шаг получает результаты предыдущего шага.
Основателем динамического программированиястал Беллман. Он предложил специальный метод решения задач ДП на основе принципа оптимальности. Согласно данному принципу оптимальное решение задачи находится путем разбиения на n-этапов, каждый из которых представляет собой подзадачу относительно одной переменой. Вычисление выполняется таким образом, что оптимальный результат одной подзадачи есть начальное решение для следующей подзадачи. Результат последней задачи есть результат всей задачи.
Формулирование задачи ДП
Дано: множество состояний, в том числе начальные и конечные;множество возможных переходов из одного состояния в другое.
Найти: оптимальную последовательность переходов из начального состояния в конечное (максимальная или минимальная сумма чисел); предполагается, что хотя бы один путь существует.
Математическая модель:
В.17 Чтобы поставленная задачи оптимального планирования приобрела количественный математический характер, необходимо ввести в рассмотрение некоторый численный критерий W. Этот критерий будет характеризовать качества, успешность, эффективность операций.
|
|
|
В зависимости от характера решаемой задачи величина W может выбираться различными способами. Например, при планировании деятельности системы промышленного предприятия в качестве критерия W может быть выбран общий годовой объем продукции или же чистый годовой доход. Критерием эффективности работы транспортной системы может быть общий грузооборот.
При отыскании оптимального планирования операцииделятся на этапы. В связи с этим процесс планирования становится многошаговым и развивается от этапа к этапу. Каждый раз оптимизируется управление только на одном шаге.
Подходы: Нисходящее (задача разбивается на подзадачи меньшего размера, они решаются и затем комбинируются для решения исходной задачи). Восходящее (подзадачи, которые впоследствии понадобятся для решения исходной задачи просчитываются заранее и затем используются для построения решения исходной задачи).
· Задача распадается на m шагов. На каждом шаге определяется показатель эффективности 
i-шаги
В задачах ДП критерий эффективности называется выигрышным.
Шаговое управление – переменные, от которых зависят выигрыши на i-ом шаге и выигрыш в целом. Нужно учитывать возможные исходы предыдущего шага, влияние управления на все последующие исходы.
Управление процессом – последовательность шагов управления.
Оптимальное управление – значение управления, при котором оно является maxили min, и состоит из множества выигрышей на каждом шаге.
В.18 Метод динамического программирования состоит в том, что оптимальное управление строится постепенно, шаг за шагом. На каждом шаге оптимизируется управление только этого шага. Вместе с тем на каждом шаге управление выбирается с учетом последствий, так как управление, оптимизирующее целевую функцию только для данного шага, может привести к неоптимальному эффекту всего процесса. Управление на каждом шаге должно быть оптимальным с точки зрения процесса в целом.
Управление на каждом шаге надо выбирать с учетом его последствий на предстоящих шагах. Это основное правило ДП, сформулированное Р. Беллманом, называется принципом оптимальности.
|
|
|
Оптимальное управление обладает таким свойством, что каково бы ни было начальное состояние на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться оптимальными относительно состояния, к которому придет система в конце данного шага.
В.19 Приведем общую схему применения метода ДП.
Предположим, что все требования, предъявляемые к задаче динамического программирования, выполнены. Построение метода ДП для решения сводится к следующим моментам:
1) Выбирается способ деления процесса управления на шаги.
2) Определяются параметры состояния Sk и переменные управления Xk на каждом шаге.
3) Записываются уравнения состояний.
4) Вводятся целевые функции K-го шага и суммарная целевая функция.
5) Вводятся условные максимумы (минимумы) Z*K(Sk-1) и условное оптимальное управление на K-м шаге: X*K(Sk-1), K =N, N-1, …, 2, 1.
6) Решаются последовательно уравнения Беллмана (условная оптимизация).
7) После выполнения условной оптимизации определяется оптимальное решение для конкретного начального состояния S0:
А) Zmax = Z*1(s0) (здесьZmax = max Z)
Б) по цепочке
Оптимальное управление: Х* =(Х1*, Х2*, …, ХN*).
В.20 Задача набора высоты и скорости. Самолет (или др. летательный аппарат), находящийся на высоте H0 и имеющий скорость V0, должен быть поднят на заданную высоту Нкон и его скорость должна быть Vкон. Известен расход горючего, необходимый для подъема аппарата с высоты Н1 на высоту Н2 при постоянной скорости, известен расход горючего при увеличении скорости при неизменной высоте. Требуется найти оптимальный режим набора высоты и скорости, при котором общи расход горючего будет минимальным.
Решение: Разобьём процесс расхода высоты и скорости на этапы. На каждом этапе самолёт увеличивает только высоту или только скорость. Состояние самолета изображается в виде точки на некоторой плоскости VOH
| V |
| Vкон |
| V |
| V0 |
| Н0 |
| Н |
| Нкон |
| S0 |
| S |
| Sкон |
|
|
|
Критерий W – расход горючего. W->min
Найдем решение задачи с помощью метода динамического программирования. Высоту разделим на n1 равных частей.ΔH=(Hкон –H0)/n1; n1=6
Скорость, которую требуется набрать разделим на n2 частей.ΔV=(Vкон –V0)/n2; n2=8
В сумме n1 и n2 будут определять количество этапов. m=n1+n2, m=8+6=14
Каждому из отрезков соответствует расход горючего в некоторых условных единицах.
Для решением методом Беллмана будем оптимизировать каждый шаг начиная с последнего. Т.о. переходя от точки к точке с права на лево и сверху вниз (от конца процесса к его началу) можно для каждой из точки выбрать условный минимум управления на следующем шаге. Т.е. направление, ведущее в Sкон с минимальным расходом горючего.
Чтобы найти из каждой точки оптимальный следующий шаг нужно проследить возможные пути из этой точки: вправо и вверх и для каждого пути найти сумму расходов на данном шаге и минимальный расход горючего на оптимальном положении. Из двух путей выбираем с наименьшим расходом горючего. Достигаем точки S0 и в результате получаем путь, указывающий движение из точки S0 в Sкон.
В.21 Задача о распределении ресурсов.
Пусть n предприятий использует некоторые ресурсы. Известно что, если K–ому предприятию выделить X единиц ресурсов, то количество произведенной продукции будет равно φk(X). Требуется распределить A единиц ресурсов между всеми предприятиями так, чтобы выпуск продукции был максимальным.
Обозначим через Xk количество ресурсов, которое нужно выделить K-му предприятию, тогда математическая модель задачи запишется так:
φ1(X1)+φ2(X2)+…+φn(Xn)→max
при ограничениях X1+X2+…+Xn=A X1≥0, X2≥0,…,Xn≥0.
Если φ1, … φn – заданы таблично, то задача решается методами динамического программирования.
Рассмотрим оптимальное распределение ресурсов с помощью метода динамического программирования. При решении задачи о распределении ресурсов введем функцию Беллмана fk(X) – максимальное количество продукции, которое могут выпустить K предприятий, при этом φk(X) – количество ресурса, получаемое K-ым предприятием при оптимальном распределении ресурса между первыми предприятиями.
Предположим, что fk(X) известна, тогда вычислим fk+1 (X). Пусть К+1–ое предприятие получает t единиц (0 ≤ t ≤ X) ресурса, тогда оно выпускает φk+1(t) единиц продукции. На долю же первых K предприятий останется X–t единиц ресурса.
В силу принципа оптимальности: чтобы получить больше продукции, необходимо распределить оптимально оставшиеся (X–t) единиц ресурса между K предприятиями. Тогда общий выпуск продукции будет равен φk+1(t)+fk(X–t). Но, чтобы этот общий выпуск продукции был максимальным, необходимо t подобрать так, чтобы эта сумма достигала наибольшего значения, т.е. fk+1(X).
|
|
|
Функциональное уравнение Беллмана:
В.22 Задача о рюкзаке — одна из задач комбинаторной оптимизации. Название получила от максимизационной задачи укладки как можно большего числа нужных вещей в рюкзак при условии, что общий объём (или вес) всех предметов, способных поместиться в рюкзак, ограничен.
В общем виде: из неограниченного множества предметов со свойствами «стоимость» и «вес», требуется отобрать некое число предметов таким образом, чтобы получить максимальную суммарную стоимость при одновременном соблюдении ограничения на суммарный вес.
Разновидности: 1) Каждый предмет из множества можно выбирать произвольное количество раз. 2) Каждый предмет можно использовать только один раз.
Задача о ранце с возможностью бесконечного выбора предметов
По данному набору из n предметов стоимостями 
и весами 
найти поднабор (с учетом того, что можно брать один предмет несколько раз) такой, что его стоимость будет максимальна среди всех поднаборов веса не более W.
Обозначим через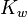 
максимальную стоимость, которую мы можем набрать при весе не более w. Получаем следующее рекуррентное соотношение:
= 0 (при весе не более нуля максимальная стоимость 0)
, где n — размер набора
Использовать рекурсию напрямую нельзя, так как появляется большое число перекрывающихся задач и время выполнения может стать экспоненциальным.
В.23 Построение кратчайших путей.
Алгоритм Дейкстры поиска кратчайшего пути
1. Начальной вершине 
присваиваем метку 
Оставшимся вершинам 
присваиваем метку 
начальную вершину окрашиваем.
2. Для каждой неокрашенной вершины связанной с последней вершиной y, дугой 
пересчитываем ее метку по формуле
В.24 Достоинства метода ДП:
1)Сравнительная простота и однотипность расчетов, что является удобным для алгоритмизации и программирования задач при их решении на ЭВМ;
2)Снижение трудоемкости решения задач за счет более полного использования свойств управляемых систем;
3)Отсутствие специальных ограничений на природу, характер и свойства функций. Они, например, могут не являться линейными, выпуклыми, непрерывными, дифференцируемыми, и могут быть заданы как таблично, так и в виде формул (аналитич).
Основной недостаток: необходимость хранения большого объема промежуточной информации. На этапе безусловной оптимизации используются условнооптимальные управления, вычисляемые и запоминаемые на предшествующем этапе условной оптимизации.
В общем виде задачи оптимального распределения ресурсов могут быть описаны следующим образом. Имеется некоторое количество ресурсов (материальные, трудовые, финансовые), которые необходимо распределить между различными объектами их использования, чтобы получить максимальную суммарную эффективность от выбранного способа распределения.Показателем эффективности может служить, например, прибыль, себестоимость, суммарные затраты и т.д.
Переход к вопросу 21!
В25. Метод главного критерия.
Заключается в том, что критерий качества связывается с одним из показателей, выбранным в роли основного (главного). На остальные показатели накладываются ограничения. В этом случае по главному показателю реализуется критерий оптимальности, по остальным - пригодности. Например, если имеется вектор полезного эффекта в виде
W<k>= <W1,W2,...,Wk>,
где W i(i=1,2...k) - компоненты вектора, например, для оборудования: производительность, экологичность, надежность, себестоимость и т.д., то метод главной компоненты заключается в произвольном выборе одного из компонентов в качестве главного, по которому производится оптимизация и выбирается решение. При этом остальные компоненты переводятся в разряд ограничений.
Этот метод прост, нагляден и часто применяется в машиностроительной практике, однако принципиальным его недостатком является произвол в выборе главного критерия. Можно привести много примеров из истории науки и техники, когда произвольный и неверный выбор этого критерия приводит к трагическим последствиям или, по меньшей мере, к малоэффективным результатам.
В26. Метод последовательных уступок.
В задачах многокритериальной оптимизации при переходе от одного варианта к другому, как правило, улучшаются значения одних критериев, но ухудшаются значения других. Компромисс разрешается введением тех или иных дополнительных ограничений или субъективных предположений. Здесь нельзя говорить об объективном единственном решении задачи; выбор наилучшего решения в значительной степени субъективен. Так как область допустимых решений очередной задачи представляет собой множество оптимальных решений предшествующих задач, то она быстро сужается до одной точки, лишая свободы выбора при максимизации последующих критериев. Следует помнить, что решение задачи оптимизации существенно зависит от результатов ранжирования критериев качества. В известной мере избавиться от этого недостатка позволяет применение метода последовательных уступок, процедура которого включает:
- расположение частных критериев в порядке их относительной важности;
- максимизацию первого, наиболее важного критерия;
- назначение величины допустимого снижения (уступки) значения этого критерия;
- максимизацию второго по важности частного критерия при условии, что значение первого критерия не должно отличаться от максимального более, чем на величину уступки;
- назначение величины уступки по второму критерию;
- максимизацию третьего критерия при условии, чтобы значения первых двух критериев не отличались от ранее найденных максимальных значений больше, чем на величины соответствующих уступок и т.д.
Здесь многокритериальная задача сводится к поочередной максимизации частных критериев и выбору величин уступок (чем уступки меньше, тем приоритет жестче); оптимальной считается любая стратегия, соответствующая условному максимуму последнего по важности критерия.
Приведенный метод широко и эффективно используется при решении задач управления в технических системах разной направленности.
27. Эксперимент его виды. Планирование эксперимента. Требования предъявляемые к факторам при планировании эксперимента.
Эксперимент в научном методе — метод исследования некоторого явления в управляемых условиях. Отличается от наблюдения активным взаимодействием с изучаемым объектом.
Виды:
Физический эксперимент — способ познания природы, заключающийся в изучении природных явлений в специально созданных условиях.
Компьютерный (численный) эксперимент — это эксперимент над математической моделью объекта исследования на ЭВМ, который состоит в том что, по одним параметрам модели вычисляются другие ее параметры и на этой основе делаются выводы о свойствах объекта, описываемого математической моделью.
Мысленный эксперимент в философии, физике и некоторых других областях знания — вид познавательной деятельности, в которой структура реального эксперимента воспроизводится в воображении.
Критический эксперимент — эксперимент, исход которого однозначно определяет, является ли конкретная теория или гипотеза верной.
Психологический эксперимент — проводимый в специальных условиях опыт для получения новых научных знаний посредством целенаправленного вмешательства исследователя в жизнедеятельность испытуемого.
Планирование эксперимента — комплекс мероприятий, направленных на эффективную постановку опытов. Основная цель планирования эксперимента — достижение максимальной точности измерений при минимальном количестве проведенных опытов и сохранении статистической достоверности результатов. Планирование эксперимента применяется при поиске оптимальных условий, построении интерполяционных формул, выборе значимых факторов, оценке и уточнении констант теоретических моделей и др.
|
|
|
