Обработка результатов экспериментов. Принятие решений после построения модели процесса

ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА заключается в применении методов мат. статистики для оценки значений разл. физ. величин характеризующих изучаемые объекты, и (или) зависимости этих величин от одного либо нсск. изменяемых внеш. условий. Обработка результатов эксперимента включает, как правило, также и определение точности данных, полученных при его проведении.

Результаты измерений обычно содержат случайные ошибки, поэтому статистич. оценки выполняют только при наличии серии измерений - т. наз. случайной выборки. Для оценки измеряемого значения к.-л. величины или исследуемой зависимости ее от внеш. условий по данным выборки рассчитывают т. наз. выборочные параметры, характеризующие статистич. распределение ошибок в проведенном эксперименте. Такое распределение, как правило, подчиняется т. наз. нормальному закону, конкретный вид к-рого определяют два параметра - выборочное среднее и выборочная дисперсия

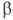Точность получаемых оценок устанавливают с помощью статистич. критериев Стьюдента (t-критерий), Фишера (F-критерий) и т. д. При этом количеств, мерами служат т. наз. доверит. вероятность и уровень значимости статистич. критерия р = 1 — . При заданных требованиях на точность результатов измерений доверит. вероятность (уровень значимости) определяет надежность полученной оценки.

Принятие решений после построения модели процесса

Нам придется принимать решения в сложных ситуациях. Решения зависят от числа факторов, дробности плана, цели исследования (достижение оптимума, построение ин­терполяционной формулы) и т.д. Количество возможных решений по примерной оценке достигает нескольких десятков тысяч. Поэтому будем рассматривать только наиболее часто встречавшиеся случаи и выделим «типич­ные» решения. Положение здесь сложнее, чем в случае принятия решений о выборе основного уровня и интер­валов варьирования факторов, где удалось рассмот­реть все варианты. Ситуации будем различать по адекватности и неадекватности модели, значимости и незначимости коэффициентов регрессии в модели, информации о положении оптимума.

Линейная модель адекватна. Здесь возможны 3 ва­рианта.

1. Все коэффициенты регрессии значимы.

2. Часть коэффициентов регрессии значима, часть не­значима.

3. Все коэффициенты регрессии незначимы.

Линейная модель неадекватна. Если линейная модель неадекватна, значит не удается аппроксимировать по­верхность отклика плоскостью. Формальные признаки (кроме величины F -критерия), по которым можно уста­новить неадекватность линейной модели, следующие.

1.Значимость хотя бы одного из эффектов взаимо­действия.

2.Значимость суммы коэффициентов регрессии при квадратичных членах . Оценкой этой суммы служит разность между b ₀ и значением зависимой переменной в
центре плана y ₀. Если разность превосходит ошибку опы­та, то гипотеза о незначимости коэффициентов при квад­ратичных членах не может быть принята.

 

В.29. В основе решения задач структурного синтеза разной сложности лежит перебор вариантов счётного множества. При переборе каждая попытка состоит из:

1)создания или поиска очередного варианта.

2)принятия решения о замене ранее выбранного варианта новым.

3)продолжения или прекращения поиска новых вариантов.

Процедуры структурного синтеза: 1) Синтез схем (принципиальных, функциональных, структурных, кинематических и др.). 2) Конструкций (определение геометрических форм, взаимного расположения деталей). 3) Процессов (технологических, вычислительных и др.). 4) Документации (чертежей, пояснительных записок, ведомостей).

Процедуры параметрического синтеза:1) Оптимизация номинальных значений параметров элементов. 2) Оптимизация их допусков. 3) Идентификация моделей. 4) Расчеты на основе упрощенных методик.

В.30 CAE — общее название для программ или программных пакетов, предназначенных для инженерных расчётов, анализа и симуляции физических процессов. Расчётная часть пакетов чаще всего основана на численных методах решения дифференциальных уравнений.

Задачи структурного синтеза при автоматизированном технологическом проектировании зависят от уровня сложности.

1-ый уровень сложности: определяется структура технологического процесса или его элементов.

2 уровень: полный перебор вариантов структуры из конечного множества. Перечень создаётся в виде технологических маршрутов.

3 уровень: решаются задачи выбора варианта структуры из множества известных вариантов. Для реш таких задач исп алгоритмы направленного перебора, последовательного, итерационного.

4 уровень: задачи решаются при активном участии технолога-проектировщика. Он занимается подготовкой исх данных и проверяет окончательный результат. Технолог, работающий в диалоге с ЭВМ, выбирает такой вариант структуры, который представляет оптимальный компромисс между производительностью работы автомата и вероятностью обеспечения заданного качества выполнения операции.

5 уровень: направлен на создание новых технологических процессов и решается в поисковых конструированиях.

В.31 (коммивояжёра) В Теории сложности выделяют массовые (в общем виде) и индивидуальные (конкретные числовые значения) задачи. Цель исследования состоит в установлении вида зависимости объёма Q требуемых вычислений от размерности задачи N. Объём вычислений может определяться числом арифметических и логических операций или затратами процессорного времени ЭВМ с заданной производительностью.

В теории сложности задачи выбора вводят понятие эффективных (с полиномиальной зависимостью) и неэффективных (с экспоненциальной зависимостью) алгоритмов.

Классы комбинаторных задач (задач дискретного программирования) в теории сложности:

1) Неразрешимые задачи (массовые задачи, решение которых полным перебором невозможно. Отделяется от др задач пределом Бреммерманаn=10^93).

2) Класс Р (относятся задачи, для которых известны алгоритмы решения полиномиальной сложности).

3) Класс NP (задачи, для которых можно за полиномиальное время проверить правильность решения).

4) КлассNP-полных задач (неизвестны полиномиальные алгоритмы точного решения, любые входящие задачи могут быть сведены одна к другой за полиномиальное время).

Из результатов теории сложности следуют практические рекомендации:

1) Приступая к решению некоторой комбинаторной задачи надо проверить не принадлежит ли она классу NP-полных задач. Если да, то не надо тратить усилия на разработку прог и алгоритмов точного решения.

2) Отсутствие эффективных алгоритмов точного решения массовых задач выбора не означает невозможность эффективного решения индивид задач из класса NP-полных или невозможность получения приближреш по эвристич алгоритмам за полиномиальное время.

В.32 Метод ветвей и границ – группа мат методов, в которых происходят операции разделения множества вариантов на подмножества и отсечение неперспективных подмножеств. В случае точного вычисления нижних границ, относиться к точным методам. Так же может быть и приближённым.

Есть множество гамильтоновых контуров и нижняя граница множества длин этих контуров, которая меньше длины самого контура. Это множество разбивается на 2 подмножества. Одно подмножество состоит из Гамильтоновых контуров, кот включ в себя дугу. Другое подмножество не содержит дугу. Для каждого подмнож нах нижнюю границу, принадлежащую контуру. Сравниваем эти нижние границы. Какое знач меньше, туда и идём. Процесс продолжается, пока в результате дробления не получат подмножество, содержащее единственный Гамильтонов контур. Нижняя граница, содержащая единственный контур, является длиной этого контура – рекорд. Получ контур просматривают и находят в них оборванные ветви дерева, сравнивают нижние границы с рекордом. Если рекорд не превышает указ нижних границ, то задача решена. Контур длины Rec является кратчайшим.

Алгоритм Литтла: 1)Приведение матрицы по строкам и столбцам, определяем нижнюю границу Гамильтонова контура. 2)Суммы констант приведения. 3)Составляем новую таблицу.

В.33 Эволюционные методы: 1)Генетический алгоритм. 2)Метод поведения толпы. 3)Метод колонии муравьёв.Холланд 1975г.

Вычисление начинается с формирования множества G–популяции. Она состоит из информационных объектов х и y – хромосом. А они в свою очередь состоят из генов х=(х1,х2,…,хn). Эволюция представляет собой многошаговый процесс. На каждом шаге формируются новые хромосомы и отбираются (селекцируются) в новые поколения.

Генетический алгоритм – метод, реализующий эволюционный поиск с использованием скрещивания.

Задача формируется таким образом, чтобы её решение могло быть закодировано в виде вектора генов (генотипа). Случайным образом создаётся множество генотипов начальной популяции. Они оцениваются с использованием «функции приспособленности», в результате чего с каждым генотипом ассоциируется определённое значение, которое определяет насколько хорошо фенотип, им описываемый, решает поставленную задачу. Из полученного множества решений (поколения) с учётом значения «приспособленности» выбираются решения (обычно лучшие особи имеют большую вероятность быть выбранными), к которым применяются генетические операторы: скрещивание, мутация, результатом чего является получение новых решений.Для них также вычисляется значение приспособленности, и затем производится отбор (селекция) лучших решений в следующее поколение. Этот набор действий повторяется итеративно. Так моделируется «эволюционный процесс», продолжающийся несколько жизненных циклов (поколений).

В.34 Теория расписаний – научная дисциплина, которая посвящена разработке методов оптимизации оперативно-календарного планирования. Задачи теории расписаний объединяют в класс задач упорядочения. Эти задачи состоят в определении оптимальной очерёдности обработки изделий на разных станках или др раб местах.

Задача упорядочения: задано множество работ или требований с определённым набором характеристик: стоимость обработки требования, длительность, момент поступления. В результате надо решить задачу дискретной оптимизации, т.е. максимизировать/минимизировать стоимость работ/время задержки.

Группы задач теории расписаний:

1) Задачи с прерываниями (когда в момент поступления нового требования старое может быть прервано, т.е. отложено с возможностью разрешения позже). 2) Задачи без прерывания (каждое требование выполняется до конца).

Методы решения задач теории расписаний:

1) Метод линейного программирования (частный случай выпуклого программирования. Симплекс-метод, относ к алгоритмам с экспоненциальной сложностью. Последовательно перебираются вершины многогранника. Метод эллипсоидов имеет некомбинаторную природу. Не перспективный).

2) Дискретное программирование (разделяют модели задач с неделимостями, экстремально-комбинаторные, задачи, имеющие особенности целевой функции).

3) Метод ветвей и границ (разделение множества на подмножества и отсечение неперспективных).

4) Сетевое планирование и управление (исп в анализе хозяйственной деятельности, для прогнозирования. Базируется на применении сетевых графиков, кот представляются в виде определённой цепи работ и событий, связанных технологической последовательностью. Метод критического пути – анализ состояния процесса в каждый заданный момент времени и определение последовательности работ).

В.35 Всегда необходимо учитывать риск и предусматривать меры для снижения уровня риска. Главная цель управления рисками: добиться, чтобы в худшем случае речь шла об отсутствии прибыли, но никак не об убытках.

Типы подходов к принятию решений:

1) Решения принимаются в условиях определённости, когда возможно с точностью определить результат каждого альтернативного решения. Сравнительно мало решений принимается в условиях определённости.

2) Решения, результаты которых не являются определёнными, но вероятность каждого возможного результата можно определить (0,1).

3) Решения, когда невозможно оценить вероятность потенциальных результатов. Это имеет место, когда мало информации о нужных факторах.

Риск – возможная опасность потерь, вытекающая из специфики тех или иных явлений природы и видов деятельности человеческого общества. Событие, которое может произойти или не произойти.

Виды риска: 1) Производственный (в сфере производства продукции, товаров и услуг). 2) Коммерческий (появляется в результате снижения уровня продаж на рынке, повышение тарифов на перевозку груза, колебания валютного курса). 3) Финансовый (во взаимоотношениях предприятий с банками, зависит от уровня заёмных средств). 4) Политические (связаны с запретом на импорт, проведением забастовок в период транспортировки груза). 5) Риск инвестиционных решений (появляется в результате инфляции).

Группы риска: 1) Возможность получения отрицательного или нулевого результата (экологич, политич части коммерческого риска). 2) Спекулятивные риски выражаются в возможности получения как отриц, так и положит результатов (финансовые).

 

В.36 Степень риска – вероятность наступления случая потерь, а также размер возможного ущерба от него. Чтобы количественно определить величину риска, нужно знать все возможные последствия отдельного действия и вероятность самих последствий.

Матрица эффектов и ущербов. Выбор решения в условиях неопределённости включает построение эффективных и ущербных матриц риска, количественную оценку вариантов. Количественная оценка риска для каждого решения при какой-либо ситуации равна разнице максимального и фактического эффекта для этой ситуации.

Типы методов управления рисками:

1) Методы уклонения от риска (отказ от ненадёжных партнёров, от рисковых проектов).

2) Локализация риска (создание подразделений для выявления рискованных проектов).

3) Диссипация риска (диверсификация видов деятельности, сбыта и поставок, инвестиций).

4) Компенсация риска (стратегическое планирование деятельности, прогнозирование внешней среды, создание системы результатов).

Критерии принятия решений:

1) Максимин (ориентир на получение гарантированного выигрыша при наихудшем состоянии внешней среды). 2) Минимакс (критерий Сэвиджа, для каждого решения выбрать максимально возможные потери, затем выбрать решение, кот ведёт к минимизации потерь). 3) Равновесный подход (критерий Лапласса, выбирается альтернатива с макс значением усреднённого по всем состояниям внешней среды). 4) Критерий Гурвица (компромисс максимин и минимакс, придаётся вес обоим результатам, вес определяется субъективно, затем умножение на веса и суммирование результатов, выбирается решснаиб результатом).

 

В.37 Одной из сфер практической деятельности, в которой успешно применяются методы системного анализа, является сфера управления запасами. Первые системы управления запасами были разработаны применительно к обоснованию необходимой потребности в запасных частях предприятий крупных компаний. Задачи управления запасами обладают одной особенностью - с увеличением запасов увеличиваются расходы, связанные с их хранением, но уменьшаются потери от возможного их дефицита. Следовательно, одна из задач управления запасами заключается вминимизации суммы ожидаемых затрат, связанных с хранением запасов, и потерь, обусловленных их отсутствием в случае необходимости.

Методика 20/80 и Методика АВС

Основная проблема, возникающая при решении задачи управления запасами, состоит в создании эффективной и надежной системы управления. Общая система управления запасами представляет собой три уровня решений.

Первый уровень предусматривает обработку, ведение учета и хранение информации о запасах.

Второй уровень предполагает разработку правил принятия решения, на основе которых устанавливаются срок и размер заказа, необходимого для пополнения запасов.

Третий уровень позволяет на основе разработанных правил принятия решений построить модель системы управления запасами и в соответствии с этой моделью определить стратегию функционирования системы на длительную перспективу.

Таким образом, задача управления запасами есть комплексная задача, составными частями которой являются ведение информационной базы,построение моделей управления запасами, оптимизация объема создаваемого запаса и времени его пополнения и прочие вопросы.

 

В.38 Модель управления запасами используется для определения времени размещения заказов на ресурсы и их количество на складах. Любая организация должна поддерживать уровень запасов, чтобы избежать издержек на производстве и в сбыте. Поддержание высокого уровня запасов избавляет от потерь, обусл их нехваткой. Закупка в больших объёмах материала необходимы для создания запасов.

Цель модели: сведение к мин отрицательных последствий накопления запасов, что выражается в определённых издержках (на размещение заказов, на хранение, на потери, связанные с недостаточным уровнем запасов).

Виды моделей:

1) Простейшая модель оптимального размера заказа (Модель Уилсона).

2) Модель оптимального размера заказа с фиксированным временем выполнения. 3) Модель планирования оптимального размера заказа (модель с производством). 4) Модель оптимального размера заказа с дефицитом.

5) Модель с количественными слитками.

Запас – любой материальный ресурс, который храниться на предприятии для удовлетворения потребностей.

Издержки заказа – издержки, связанные с переналадкой оборудования и подготовительными операциями.

Издержки хранения – расходы, связанные с содержанием товара на складе.

Упущенная прибыть (издержки дефицита) – издержки, связанные с отсутствием продукта на складе.

Совокупные издержки – сумма издержек заказа.

Точка восстановления – уровень запаса, при котором делается новый заказ.

 

 

В.39 Типы спроса:

1) Детерминированный: статический и динамический.

2) Стохастический: стационарный и нестационарный.

1) известен заранее, в отличие от 2). При статич интенсивность потребления ресурса остаётся неизменна во времени, в отличие от динамич. При стац спросе функция плотности вероятности неизменна во времени в отличие от нестац.

Обзор существующих направлений в моделировании управления запасами:

1) Большинство систем управления запасами включают сотни и тысячи продукции. Целесообразно ограничиться товарами, которые обладают высокой годовой стоимостью продаж. Для моделирования товаров нескольких видов разработаны многопродуктовые модели.

2) Проблемы, связанные с наличием, могут осложниться при ограничениях на складские мощности.

3) На практике спрос и время поставки чаще являются вероятностными величинами. Для формализации фактора неопределённости делают предположение о законе распределения. Чаще это нармальное распределение или распределение Пуассона.

4) Особо сложными являются случаи, когда система управления запасами включает сразу много объектов. Наиболее перспективнымиявл не аналитич, а имитационные модели.

5) Важным моментов является выбор критерия эффективности.

 

В.40 Детерминированная модель –описывает процессы, в которых не учитываются случайные факторы.

Простейшая модель Уилсона – система с фиксированным размером запаса. Не является универсальной, но помогает понять поведение запаса во многих практических случаях, позволяет регулировать и контролировать уровень запаса. На практике модель модифицируется. Основная сложность состоит в правильном определении входных параметров задачи, т.к. не всегда они задаются в численном виде или явном.

Примеры решения задач управления запасами:

1) Задача о загрузке (задача о рациональной загрузке судна, самолета, которое имеет ограничения по объему или грузоподъемности. Каждый помещенный на судно груз приносит определенную прибыль. Задача состоит в определении загрузки судна такими грузами, которые приносят наибольшую суммарную прибыль).

2) Замены оборудования (определение оптимального срока эксплуатации механизма).

3) О планировании рабочей силы (При выполнении некоторых проектов число рабочих, необходимых для выполнения какого-либо проекта, регулируется путем их найма и увольнения. Поскольку как наем, так и увольнение рабочих связано с дополнительными затратами, необходимо определить, каким образом должна регулироваться численность рабочих в период реализации проекта).

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: