 |
Моделирования чисел с экспоненциальным законом распределения.
|
|
|
|
Кафедра АСУ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению лабораторных работ по курсу
Моделирование систем
для студентов направления подготовки 09.03.02 «Информационные системы и технологии»
Донецк ДОННТУ
Содержание
Лабораторная работа № 1……………………………………………………4
Лабораторная работа № 2………………………………………………..…..9
Лабораторная работа № 3…………………………………..…………...….18
Лабораторная работа № 4……………………………………………………27
Лабораторная работа № 5………………………………………………..…..32
1 Лабораторная работа "Формирование псевдослучайных чисел с заданным законом (базово последовательности) распределения и проверка качества псевдослучайных чисел".
Цель работы: приобретение практических навыков генерации и проверки качества базовых псевдослучайных последовательностей чисел, получение практических навыков формирования на ЭВМ псевдослучайных чисел с заданным законом распределения в простейших имитационных алгоритмах.
1.1 Формирование базовой последовательности псевдослучайных чисел".
Выполнение работы предполагает два этапа. Первый этап включает составление алгоритма и программы для непосредственной генерации случайных чисел, равномерно распределены в интервале (0,1) по предоставленному преподавателем методу формирования псевдослучайной последовательности, а также использование готовых подпрограмм, позволяющих обрабатывать полученную последовательность и выдавать на экран компьютера результаты этой обработки. При составлении программы могут быть использованы следующие методы формирования последовательности случайных чисел:
|
|
|
- Встроенная функция случайных чисел используемого языка формирует псевдослучайное число при каждом выполнении оператора, в котором эта функция вызывается как выражение или как элемент выражения. При многократном обращении к функции при выполнении программы формируется последовательность различных псевдослучайных чисел. При последующих запусках программы повторяется эта же последовательность (с одной и того же начального числа).
- Вариант(1). Метод “середины квадратов”.
- Вариант (2).Метод “середины произведений”.
- Вариант (3).Типовая программа по методу Коробова, представлена с помощью ряда операторов, безотносительно языка программирования.
r=g*h;
a=r/p;
x= a – целая часть от (a);
h=r – p * целая часть от(a),
Где x – искомое значение псевдослучайной величины;
p,g – константы, которые необходимо задать в начале программы; Эти константы могут принимать разные значения (но с особыми требованиями, мы их не будем касаться), и от их значений последовательность будет принимать различный вид. Рекомендовано выбирать p=2027,g=1010.
h – некоторая переменная, которая на каждом шаге алгоритма пересчитывается. Во время первого вызова программы необходимо положить h = 1.
- Вариант (4). Типовая программа для ЕОМ – представлена следующим набором операторов
t=v1+v2;
if t<4 then goto 10;
t=t-4;
10: v1=v2;v2=t; x=t/4;
Где:
x- искомое значение псевдослучайной величины;
v1,v2 - константы, которые необходимо задать в начале программы.
Рекомендуется выбирать v1 =3.14159 v2 =0.542101.
- Вариант (5). Линейный конгруэнтный метод. В качестве значения случайного числа выделяют остаток от деления произведения предыдущего случайного x i-1 и числа a (постоянного множителя)
xi = (a * x i-1) mod m
где:
a, m - постоянные числа;
xi - случайное число;
x = xi / m
x- искомое значение псевдослучайной величины.
Рекомендуется выбирать a= 15133, m =27119.
- Вариант (6).Смешанный конгруэнтный метод. Этот метод отличается от предыдущего тем, что к предыдущему случайному числу прибавляется постоянное число m.
|
|
|
xi = (a * x i-1 + m) mod m
- Вариант (7).Обобщенный конгруэнтный метод.
7.а – j=2; 7.б – j=3; 7.в – j=4;
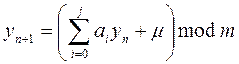

Где:
a0, a1,..., aj – множители;
µ - значение инкремента;
y1, y2,..., yn - получаемые случайные числа;
ξ- искомое значение псевдослучайной величины.
- Вариант (8).Комбинированный метод. Выбирается два x1, x2 числа в диапазоне [0,1]. Далее производятся вычисления
v1=2*x1- 1;
v2=2*x2- 1;
s=v12+v22;
если s>1, то x= s-1, иначе x=s;
для следующего шага
x1=x2;
x2=x.
1.2. Порядок выполнения работы на ЭВМ.
- Выбрать метод формирования базовой последовательности согласно варианту.
- Разработать алгоритм формирования выборки базовой последовательности псевдослучайных чисел.
- Составить программу для формирования псевдослучайных чисел.
- Провести набор программы и состыковать ее с подпрограммами.
- Для проверки качества получаемых псевдослучайных чисел использовать программы, разработанные при изучении курса «Теория вероятностей», которые позволяют рассчитать оценки математического ожидания, дисперсии (среднеквадратичного отклонения), построить гистограмму, оценить выбранный закон с помощью критерия Пирсона.
- Провести рабочий запуск всей программы при количестве чисел более 100.
- Изменить значения исходных данных или используемых коэффициентов и оценить получаемые результаты.
1.3 Содержание отчета.
- Описание заданного программного метода генерации псевдослучайной последовательности и блок схема алгоритма;
- Текст программы для реализации алгоритма на ЭВМ.
- В качестве результатов представить набор полученных чисел в количестве 10-20, результаты проверки качества.
- Анализ полученных результатов, включая построение гистограммы и таблицы частот, расчет достоверности и количества реализаций, сравнительный анализ различных методов.
- Выводы по работе.
1.4 Контрольные вопросы.
- Назначение базовых последовательностей случайных чисел.
- Требования к их качеству;
- Суть табличных, аппаратных и программных средств генерации случайных последовательностей.
- Понятие "псевдослучайная последовательность" и "квазиравномерное распределение";
|
|
|
- Основные свойства и параметры равномерно распространенных в интервале от 0 до 1 чисел.
- Методы проверки качества псевдослучайных последовательностей;
- Методы фиксации и обработки результатов статистического моделирования и их программная реализация (по тексту программы);
- Нахождение количества реализаций при статическом моделировании; Анализ результатов, полученных в данной работе.
2 Лабораторная работа "Формирование псевдослучайных чисел с различными законами распределения и проверка качества псевдослучайных чисел".
Цель работы: приобретение практических навыков формирования на ЭВМ псевдослучайных чисел с заданным законом распределения в простевших имитационных алгоритмах.
2.1 Формирование последовательностей псевдослучайных чисел с заданными законами распределения. Теоретические сведения.
Моделирования чисел с равномерным законом распределения.
Для моделирования чисел с равномерным законом распределения воспользуемся методом обратной функции.
Характеристики равномерного закона.
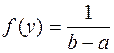 ;
;
 ;
;
Используемая формула
 ;
; 
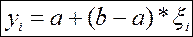
Моделирования чисел с экспоненциальным законом распределения.
Характеристики закона.
 ;
;
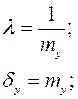
Используемая формула
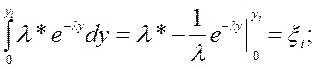
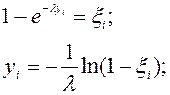

Моделирования чисел с нормальным законом распределения.
Характеристики закона.

Для моделирования нормального распределения пользуются центральной граничной теоремой, которая говорить: пусть есть некоторая последовательность СЧ с одним законом распределения (Хі). Если с этой последовательности брать по n чисел и находить их сумму y=x1+x2+…+xn, то полученные при этом числа y при n®∞, будут подчиняться нормальному закону распределения.
Если математическое ожидание чисел х равно mx и дисперсия равна Dx,
то математическое ожидание чисел y равно mx*n, дисперсия Dy=Dx*n2.
Для получения последовательности чисел, удовлетворяющих нормальному закону распределения, достаточно принимать n равным 8-12 чисел.
Базируясь на этой теореме, можно разработать алгоритм, который позволял бы получать 1 число с нормальным законом распределения.
|
|
|
 |
где: 

Моделирования чисел, распределенных по закону Пуассона.
Характеристики закона
Закон Пуассона:
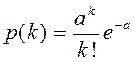 ;
;
Воспользуемся граничной теоремой Пуассона.
Пусть есть некоторый случайный опыт А, для которого известно Рn- вероятность положительного исхода при одном опыте.
Если проводить серию независимых опытов, то количество опытов К, в которых опыт свершился, при общем количестве испытаний N→∞, а Рn→0 будут подчинятся закону Пуассона.
Реализовать эту теорему можно, по следующему алгоритму.
 |
Чтобы иметь числовое значения вероятности Pn и количества испытаний n, поступают следующим образом: задаются чем-нибудь, или это Pn, или это n, обращая внимание на следующие рекомендации.
Pn берут в пределах: Pn=(0.1- 0.01).
а= Pn*n.
n=5 – 20 реализаций.
Вторую величину рассчитывают.
2.2 Порядок выполнения работы.
- Составить простейший имитационный алгоритм, позволяющий промоделировать описанный в задании процесс, включающий формирование случайных чисел с заданным законом распределения, отличным от равномерного распределения в интервале от 0 до 1. Для формирования базовой последовательности использовать стандартный генератор языка программирования.
- Выбрать метод формирования последовательности согласно варианту.
- Разработать алгоритм формирования псевдослучайных чисел.
- Составить программу для реализации имитационного алгоритма и соединить ее с подпрограммами, которые проверяют качество полученных чисел.
- Для проверки качества получаемых псевдослучайных чисел использовать программы, разработанные при изучении курса «Теория вероятностей», которые позволяют рассчитать оценки математического ожидания, дисперсии (среднеквадратичного отклонения), построить гистограмму, оценить выбранный закон с помощью критерия Пирсона.
2.3 Варианты заданий
Варианты заданий для составления простейших алгоритмов приведены в таблице 2.1
Таблица 2.1. Варианты заданий
| № | Описание процесса | Искомый результат |
| На сборочном участке последовательно собираются узлы, состоящие из трех деталей. Время присоединения одной детали - случайная равномерно распределенная величина с параметрами Мр та Dp (мин.). Длительность рабочей смены- 8 час. | Найти среднесменный выпуск готовых узлов | |
| На сварочном стане свариваются трубы, состоящие из двух металлических листов. Длина листов подчиняется нормальному закону с параметрами Мн и Dн (см.). Разница случайных длин каждой пары листов обрезается и идет в отход. | Найти среднюю длину отходов, приходящихся на каждую трубу. | |
| В ремонтном участке поступает поток оперативных заявок на ремонт, суточное количество которых распределено по закону Пуассона с параметром Мп. Участок может обслужить не более 2 заявки в день. | Найти среднее количество заявок, поступающих за неделю, и заявок, не обслуженных за неделю (6 дней). | |
| В ОТК поступают для обработки детали, которые имеют случайное отклонение от номинального размера, распределенные по экспоненциальному закону с параметром Мэ (мм.). Если это отклонение превосходит допуск, равный Мэ, деталь идет в брак. | Найти процент бракованных деталей. | |
| На прокатном стане изготовляются листы, длина которых есть случайная величина, которая имеет нормальный закон распределения с параметрами Мн и Dн (м.). Длина готового изделия, согласно ГОСТу, может быть равной L1, L2, или L3. Листы, которые имеют отличные от указанных длин размеры, обрезаются или идут во второй сорт. (длины изделий рассчитываются: L1=Mн+Dн; L2=Mн; L3=Mн-Dн | Найти среднюю длину отходов, которые приходятся на один лист, и процент листов второго сорта. | |
| На химическом комбинате готовую продукцию из реакторов, объёмом 200т., вывозят на склад поездами со спецвагонами. В такой вагон вмещается продукция, объём которой – случайная величина с равномерным законом распределения с параметрами Мр и Dр (т.). | Найти максимальную длину поезда, необходимую для разгрузки реактора. | |
| Проводится проверка измерительного устройства путем измерения некоторого параметра с помощью проверяемого устройства и устройства более высокого класса. Разница между этими двумя показаниями являются случайной величиной с экспоненциальным законом распределения и параметром Мэ. Если эта разница меньше Мэ, то устройство пригодно к использованию, если она лежит между Мэ и 2Мэ –отправляется на корректировку, если больше чем 2Мэ- отбраковывается. | Найти процент годных, откоррек-тированных и отбракованных измерительных приборов. | |
| На сборочный участок через промежуток времени 5мин. Находят партии деталей, величина которых подчиняется закону Пуассона с параметром Мп. Для сборки одного изделия требуется 5 деталей. | Найти количество моделей, собранных за смену (8 ч.) | |
| Стороны прямоугольников имеют случайные размеры, равномерно распределены с параметрами Мр и s p (см). Прямоугольники разрезают на квадраты со сторонами 1х1 (см) | Найти процент отходов | |
| Грузовики через промежуток времени 10 минут привозят руду на комбинат, объем которой подчиняется нормальному закону с параметрами Мн и нs. | Сколько руды привозят грузовики в среднем за сутки | |
| Ко входу информационного прибора через промежуток времени 10 минут поступают сигналы, размер которых подчиняется нормальному закону с параметрами Мн и s н (mb). Прибор может обработает за час 6 * Мн mb информации. | Найти процент, необработанной информации | |
| В цехе фабрики изготавливают продукцию, которая фасуется в ящики. В час производится случайное количество ящиков, которое подчиняется закону Пуассона с параметром Мп. Каждые два часа из цеха вывозят партии по 10 ящиков. | Сколько в среднем ящиков остается в цехе за сутки | |
| На склад через каждые пять минут приходит партия сырья, объем которой подчиняется равномерному закону с параметрами Мр и sр. | Определить какой должен быть объем резервуара, чтобы в него помещалось сырье, приведенное за час. | |
| Стороны прямоугольников имеют случайные размеры, нормально распределены с параметрами Мн и sн (см). Из прямоугольников вырезают круги с радиусом 2 (см) | Найти процент отходов исходного материала. | |
| На склад завода автомобили через промежуток времени 10 минут привозят сырье, объем которой подчиняется нормальному закону с параметрами Мн и sн(т). Завод расходует каждый час 1000т. | Определить хватает ли сырья на каждый час |
|
|
|
Численные параметры к вариантам заданий приведены в таблице 2.2.
Таблица 2.2 Численные параметры к вариантам заданий.
| № | Виды законов распределения | |||||
| Равномерный | Нормальный | Пуассона | Экспоненциальный | |||
| Мр | sр | Мн | sн | Мп | Мэ | |
| 1/√3 | 0,1 | |||||
| 2/√3 | 0,2 | |||||
| √3 | 0,4 | |||||
| 1/√3 | 0,5 | |||||
| 2/√3 | ||||||
| √3 | 0,5 | 1,5 | ||||
| 2/√3 | 0,6 | |||||
| √3 | 0,7 | 2,5 | ||||
| 2/√3 | 0,8 | |||||
| 2/√3 | 0,9 | 3,5 | ||||
| √3 | ||||||
| 2√3 | 4,5 | |||||
| 2/√3 | ||||||
| √3 | 0,5 | |||||
| 2√3 | 0,7 | 6,5 | ||||
| 3√3 | 0,8 | |||||
| 0,9 | 7,5 | |||||
| 2√3 | ||||||
| 3√3 | 4,5 | |||||
| 2√3 | 0,5 | |||||
| 3√3 | ||||||
| 1/√3 | 0,5 | 6,5 | ||||
| 3√3 | 0,6 |
2.4 Содержание отчета
- Условие задачи.
- Описание метода получения заданных случайных чисел и необходимые вычисления по преобразованию чисел, равномерно распределенных в интервале (0,1), в заданную последовательность чисел.
- Блок-схема алгоритма решения задачи с подробным описанием операторов получения случайных чисел согласно выбранному методу; описание блок-схемы.
- Программа и результат ее решения.
- Обработка полученных результатов (гистограммы и результата сравнения полученного распределения с заданным по критерию).
2.5 Контрольные вопросы
1.Свойства и параметры наиболее распространенных законов распределения (равномерного, нормального, экспоненциального, пуассоновского).
2.Сущность и программная реализация методов формирования псевдослучайных чисел с равномерным, нормальным, экспоненциальным и пуассоновским законами распределения.
3.Методика выбора и расчета исходных параметров для приближенных программных методов моделирования нормального и пуассоновского распределения.
4.Логика построения и программная реализация имитационного алгоритма для решения индивидуального задания по данной работе
3.Лабораторна работа "Моделирование испытаний в схеме случайных событий."
Цель работы: получение практических навыков имитационного моделирования случайных событий и работы с простейшими имитационными моделями.
3.1. Теоретические положения
Моделирование одиночного случайного события.
Для того, чтобы получить последовательность одиночных случаев А с вероятностью наступления Р, необходимо получить базовую последовательность случайных чисел x, равномерно распределенных от 0 до 1, и сравнивать их с вероятностью Р. Если случайное число меньше Р, считать, что событие А произошло, иначе – не произошло.

Рисунок 3.1 Алгоритм моделирования случайного события.
Моделирование полной группы событий.
Для моделирования полной группы событий необходимо иметь массив из чисел - вероятностей наступления каждого события для полной группы событий. Затем необходимо получить случайное число x. (0 <x <1). Сравниваем x с РА1. Если оно меньше, то произошло событие А1, иначе сравниваем x с РА1 + РА2. Это сравнение продолжается, пока сумма вероятностей станет больше x. Происходит событие, вероятность которой прибавилась последней.
 |
|
|
|
12 |


