Главная | Обратная связь | Поможем написать вашу работу!

Моделирование зависимых испытаний

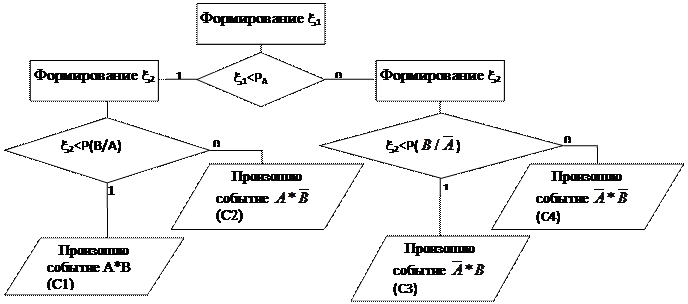Пусть задано событие А происходящее с вероятностью Р_А и событие В происходящее с вероятностью Р (В/А) при условии, что А произошло, и с вероятностью Р (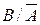) при условии, что а не случилось.

Рисунок 3.4 Алгоритм моделирования зависимых испытаний.

3.2. Описание работы.

Для выполнения работы необходимо выбрать метод моделирования случайных событий согласно индивидуальному заданию, условия которого приведены в табл. 3.1. При выполнении работы необходимо;

- Предусмотреть выдачу на экран текущих данных о результате каждого испытания: порядкового номера текущей реализации, условного номера события и его теоретическую вероятность, текущего значения базовой псевдослучайной величины, равномерно распределенной от 0 до 1, результата моделирования испытания на данной реализации.

- Организовать сбор статистических данных для расчета оценок исходных вероятностей и дальнейшего сравнения полученных оценок и исходных вероятностей;

- Сравнить полученные оценки вероятностей случайных событий с заданными вероятностями и найти погрешность Δ= │Р-Р1│;

- Сравнить результаты моделирования с результатами аналитического решения задачи и проанализировать возможные причины различия.

3.3. Порядок выполнения работы на ЭВМ.

- Составить простейший имитационный алгоритм, позволяющий промоделировать описанный в задании процесс и определить искомую величину. Для формирования базовой последовательности использовать стандартный генератор языка программирования.

- В алгоритме предусмотреть сбор данных для расчета оценки заданных вероятностей.

- Набрать и отредактировать программу.

- Сделать пробный запуск программы при количестве реализаций N = 20. При нахождении ошибок исправить их и повторить запуск.

- Провести рабочий запуск модели при заданном количестве реализаций N> = 100. При этом наблюдать за результатами текущих испытаний, зафиксировать 10-15 испытаний и общие результаты моделирования.

- Провести расчеты оценок всех вероятностей и сравнить их с заданными. При нахождении большого количества различий исправить программу и снова запустить программу

- Заключительные результаты работы представить на проверку преподавателю.

3.4 Содержание отчета

- Условие задачи.

- Описание метода моделирования.

- Блок-схема моделирующего алгоритма с пояснениями.

- Программа, написанная на алгоритмическом языке и результаты ее решения на ЭВМ.

- Сравнение полученных оценок вероятностей с заданными.

- Расчет искомых величин аналитическим путем и сравнения результатов моделирования и расчета.

- Выводы из работы.

Таблица 3.1. Условия индивидуальных заданий.

	Условия заданий	Искомая величина
	Проводится бомбометания по трем составам боеприпасов. При сбросе одной бомбы вероятность попадания в первый состав 0.1, во второй - 0.2, в третий - 0.4. при попадании в один состав с вероятностью 0.5 подрываются каждый из двух последних.	Найти вероятность того, что при сбросе одной бомбы будут взорваны все три состава.
	По линии связи передаются сообщения 5 типов, отличающихся объемом. Вероятность передачи каждого типа сообщений соответственно равны 0.1; 0.2; 0.4; 0.15; 0.15, а объемы - 100Кб; 70Кб; 50Кб; 20Кб; 10кб. Каждое из сообщений с вероятностью 0.1 может потеряться. Сообщения передаются через промежутки времени, равные 5 мин.	Найти средний объем информации, переданной за час.
	Длина листов может иметь размеры 3.0; 3.1; 3.2; 2.9; 2.8 (м.) С вероятностями 0.03; 0.2; 0.5; 0.25; 0.02. из двух листов сваривается труба и, если размеры листов разные, разница идет в отход.	Найти процент отходов
	На склад приходят самосвалы 4 видов. Вероятности прихода каждого из них имеют значение 0.1; 0.2; 0.4; 0.3. грузоподъемности каждого из видов: 10т; 15т; 20т; 25т. интервал между приходами самосвалов постоянный и равный 10 мин. С вероятностью 0,08 каждый самосвал может быть недогруженный на 5 процентов.	Найти общее количество груза, привезенного самосвалами на склад в среднем за смену
	Проводится стрельба по мишени. Вероятность попадания в первую зону - 0.7; во вторую - 0.15; в третью - 0.1. вероятность промаха - 0.05. за попадания в каждую зону стрелок получает соответственно 100, 50, 20 (очков).	Найти вероятность того, что за три выстрела стрелок получит более 100 очков.
	На ВЦ имеется три компьютера. В момент получения задания каждый из них может быть занятым с вероятностью 0.8. Если в момент получения задачи нет свободных компьютеров, задания по вероятностью 0.3 не обрабатывается, с вероятностью 0.5 пересылается на вспомогательный компьютер, или вероятностью 0.2 ждет.	Найти процент необработанных задач
	К телеграфной станции через промежутки, равные 5 мин., поступают сообщения 5 видов. Вероятность появления каждого вида соответственно равна 0.4; 0.2; 0.1; 0.2; 0.1, а объемы - 200Кб, 500кб, 1Кб, 1.5Кб, 2Кб. С вероятностью 0,08 каждое сообщение может быть ошибочным.	Найти процент ложной информации.
	На участке с трех одинаковых деталей складируется изделие. Каждая деталь может быть первого, второго или третьего сорта с вероятностями 0,5; 0.3; 0.2. если в изделие попадают две или более деталей третьего сорта, то он сам попадает в третий сорт, если все три детали первого сорта, то все изделие первого сорта, иначе изделие относится ко второму сорту.	Найти процент первого, второго и третьего сорта.
	Проводится три выстрела по одной мишени. Вероятность попадания при первом, втором и третьем выстрелах соответственно равна 0.4; 0.5; 0.7	Найти вероятность того, что в мишени после трех выстрелов лишь одна пробоина.
	По самолету производится три отдельных выстрела, вероятность попадания каждый раз равна 0.3. Для выхода самолета из строя достаточно трех попаданий. При одном попадании самолет выходит из строя с вероятностью 0.2; при двух попаданиях - 0.6.	Найти вероятность того, что самолет будет выведен из строя при 3 выстрелах.
	Каждая информационная посылка состоит из 10 последовательно передаваемых сигналов. Вероятность передачи ошибки каждый раз равна 0.1. Если в сообщении окажется меньше 3 ошибок, то сообщение восстанавливается полностью, если их более 7, то теряется, в других ситуациях восстанавливается с вероятностью 0.3	Найти вероятность передачи правильного сообщения.
	Линия передачи, составленная из 5 независимых каналов. В момент поступления сигнала каждый из каналов может быть занят с вероятностью 0.7; 0.3; 0.8; 0.5; 0.6. Если все каналы заняты, сигнал с вероятностью 0.4 потеряется, с вероятностью 0.2 дождется передачи и с вероятностью 0.4 задействуется на резервном канале	Найти процент передаваемых сигналов.
	В ремонтное депо приходят трамваи с поломками 3х видов. Вероятности прихода каждого из видов имеют значение 0.1; 0.2; 0.7. Трамваи с поломками первого вида с вероятностью 0,5 может уйти без ремонта, а другого вероятностью 0,5 могут изменить вид на третий. Время ремонта зависит от вида ремонта и равна 40 мин., 50 мин., 70хв.	Найти количество времени, в среднем необходимо для ремонта 10 трамваев..
	На линию связи, состоящий из 2 каналов, через равные промежутки времени поступают сообщения. Каждый раз каждый из каналов может быть занят с вероятностью 0.4, свободным с вероятностью 0.5, поломанным с вероятностью 0.1. Если оба канала не могут передать сообщение, оно с вероятностью 0.4 теряется.	Найти процент потерянных сообщений.
	Код передаваемого сообщения состоит из 6 разрядов. Вероятность ошибки в каждом из разрядов - 0.1. Если в сообщении, передается ложные два или менее из 4 первых разрядов, но не ложные два последних - сообщение восстанавливается полностью, если в той же ситуации есть еще одна ошибка в последних разрядах, то сообщение восстанавливается с вероятностью 0.5. Во всех других случаях сообщения не восстанавливается.	Найти процент правильно переданных сообщений.
	Прибор состоит из 3 узлов (А, В, С). Вероятность выхода из строя узла А равна 0.1. Вероятность выхода из строя остальных узлов зависит от состояния узла А. Если узел А исправен, то вероятности выхода из строя узлов В и С равны соответственно 0.05 и 0.09. При выходе из строя узла А последние вероятности принимают значения 0.20 и 0.15. Найти вероятность безотказной работы прибора, если он считается исправным с хотя бы двумя исправными узлами.	Найти вероятность безотказной работы прибора, если он считается исправным с хотя бы двумя исправными узлами.
	Работа двигателя контролируется двумя регуляторами. При работе обоих регуляторов двигатель отказывает с вероятностью 0.05, при работе только первого из них - с вероятностью 0.08, при работе только второго - с вероятностью 0.09, при отказе обоих - с вероятностью 0.1. Первый регулятор вероятность безотказной работы 0.98, а второй - 0.95.	Найти вероятность безотказной работы всего устройства.
	Наблюдение за объектом ведется с помощью 2 станций для наблюдения, вероятность безотказной работы которых во время некоторого времени t соответственно равна 0.95 и 0.98. Если обе станции работают, то вероятность получить ложную информацию об объекте равна 0.05. Если первая станция вышла из строя, то такая вероятность равна 0.1, а если второй - то 0.15.	Найти вероятность получения ложной информации об объекте
	В механический цех поступают листы металла. Длина листов может иметь размеры 9.1; 9.5; 10; 10.5; 11 (метров) с вероятностью 0.2; 0.1; 0.4; 0.1; 0.2. Согласно стандарту длина может быть 9, 10 или 11 метров. Разница отрезается и поступает в отход. С вероятностью 0.05 каждый лист может быть бракованным и также идет в отход.	Найти процент отходов.
	Проводится стрельба по мишени. Каждый стрелок имеет три попытки. Вероятность попадания на первой попытке в первую зону - 0.6; во вторую - 0.2; в третью - 0.1. вероятность промаха - 0.1. На каждой последовательной попытке вероятности попаданий растут на 10%. За попадания в каждую зону стрелок получает соответственно 100, 50, 20 (очков).	Найти вероятность того, что за три выстрела стрелок получит более 100 очков.
	В регистратуре больницы направления выдаются с помощью компьютера. Пациенты могут быть двух типов с вероятностью 0,3 и 0,7. Каждый из компьютеров в этот момент может быть занят с вероятностью 0,5. Тогда пациент может передумать и уйти - первого типа с вероятностью 0,1, второго - 0,15.	Найти процент пациентов, получивших направления.
	Происходит наблюдение за объектом с помощью станции для наблюдений. Объект может находиться в одном из трех возможных состояний, случайно переходя из одного состояния в другое согласно матрицы переходов. Р= . Станция для наблюдений передает информацию об объекте с ошибкой, вероятность появления которого зависит от состояния, в котором находится объект, и равны соответственно 0.01; 0.02; 0.02.	Найти процент неправильно переданной информации.
	Прибор может находиться в одном из 4 состояний. Переход из одного состояния в другое осуществляется при поступлении на вход прибора импульсов, интервал поступления которых постоянный и равен 1 мин., согласно матрицы переходов: Р= При попадании прибора во второе состояние на выходе формируется импульс	Найти среднее значение периода следования импульсов на выходе прибора.
	Система управления под действием сигналов может переходить в один из трех возможных уровней согласно матрицей переходов Р= При работе на первом уровне задействуется 0.3 части технических средств, на втором - 0.5, на третьем -весь комплекс.	Найти коэффициент нагрузки технических средств
	Линия связи состоит из трех основных каналов и одного резервного. В момент поступления сообщения могут быть заняты: первый канал с вероятностью 0.7; второй - с вероятностью 0.8; третий -с вероятностью 0.85; резервный - с вероятностью 0.1. Резервный занимается, если 3 основные заняты, но может передавать с ошибкой, вероятность которой 0, 25. Если же все каналы заняты, то сообщение теряется	Найти процент неправильно переданной информации и потерянной информации.

3.5 Контрольные вопросы.

- Понятие и характеристики случайных событий (независимых, зависимых, полной группы) и цепи Маркова.

- Суть и программная реализация методов моделирования случайных событий.

- Суть реализация методов моделирования цепей Маркова.

- Методика обработки результатов моделирования случайных событий.

- Методика расчета необходимого количества реализаций при моделировании случайных событий.

- Методика и результаты аналитического решения задачи, их сравнение с результатами моделирования.

- Анализ результатов, полученных в этой работе.

4 Лабораторная работа "Моделирование систем массового обслуживания методом последовательной проводки."

Цель работы: приобрести практические навыки исследования систем массового обслуживания (СМО) методом имитационного моделирования с использованием универсальных алгоритмических языков.

4.1. Описание работы.

Для реализации работы на ЭВМ студент должен предварительно составить алгоритм согласно выбранному методу решения задачи, составить полную программу для моделирования заданного варианта СМО и осуществить ее запуск.

4.2. Варианты индивидуальных заданий.

Перед выполнением лабораторной работы студентам выдается задание из числа вариантов, приведенных в табл. 4.1.

Законы распределения в табл. 4.1 обозначены следующим образом: Э экспоненциальный; Н нормальный; Р равномерный. Рядом указывается численное значение параметров закона. Для экспоненциального закона – математическое ожидание, для равномерного и нормального математическое ожидание и СКО (через дробь)

4.3 Порядок выполнения работы.

- Согласно данным вариантам составить моделирующий алгоритм для нахождения искомых характеристик СМО.

- Составить программу.

- Предусмотреть вывод на экран всех основных параметров, характеризующих моделируемый процесс (номер реализации, интервал между моментами поступления заявок, момент поступления заявок, момент освобождения канала от обслуживания предыдущей заявки и т.д.).

- Набрать программу модели СМО на ЭВМ.

- Провести пробный прогон программы при количестве реализаций 10-15 в пошаговом режиме.

- Провести проверку правильности работы программы, при необходимости исправить ошибки и неточности.

- Провести рабочий прогон программы с количеством реализаций 100-200. Первые 10 реализаций выполнить в пошаговом режиме.

- По результатам построить временные диаграммы.

- Последующие реализации выполнить в циклическом режиме. Зафиксировать 10 последних текущих результатов и окончательные результаты моделирования, которые предоставить на проверку преподавателю и сверить с результатами аналитического расчета.

- Полученные результаты моделирования сравнить с результатами аналитического расчета или контрольными цифрами, выданным преподавателем. Проанализировать причины различия этих результатов.

- По указанию преподавателей путем сравнения результатов моделирования подобных СМО, полученных студентами, оценить влияние параметров СМО (интенсивность развития и обслуживания заявок, количества каналов и т.д.) и дать предложения об улучшении этих показателей.

4.4 Содержание отчета

- Индивидуальное задание согласно полученным вариантом.

- Блок-схема моделирующего алгоритма данной СМО.

- Полная распечатка программы.

- Результатами моделирования.

- Расчет необходимого количества реализаций.

- Анализ полученных результатов.

- Выводы (о точности полученных результатов, о возможных путях улучшения характеристик данной СМО и об эффективности моделирования).

4.5 Контрольные вопросы

- Методы моделирования СМО.

- Какие характеристики СМО находятся с помощью метода "последовательной проводки заявок"?

- Как находится необходимое количество реализаций моделирующего алгоритма?

- Что выбрано в качестве единичной реализации данной модели?

- Особенности моделирования СМО с ограниченным ожиданием.

- Особенности моделирования СМО с выбором каналов по жребию.

- Анализ результатов моделирования по данной лабораторной работе

- Ответы на вопросы иллюстрируются примерами из отчета о данной лабораторную работу.

Таблица 4.1 Задания на лабораторную работу по моделированию СМО методом последовательной проводки заявок

Номер	Тип СМО	Выбор заявок из очереди	Выбор каналов	Интервал поступления	Время ожидания	Время обслуживания	Определить
	1 канальная	В порядке поступления	-	Н 5 мин/ 1	Э 10 мин	Э 5мин	Ср. время ож., Ср. время пр., Вер. отказа
	1 канальная	В порядке поступления	-	Э 5мин		Р 5 мин./0,5	Ср. время пр., Вер. отказа
	2 канальная	В порядке поступления	По приоритету (в обратном порядке номеров)	Р 5 мин./0,5	¥	Н 10 мин/2	Ср. время ож., Ср. время пр.,
	2 канальная	В порядке поступления	Мин.время освобождения	Н 5 мин/ 1	Э 10 мин	Э 10 мин	Ср. время ож., Ср. время пр., Вер. отказа
	4 канальная	В порядке поступления	По жребию	Р 5 мин./0,5	¥	Н 20 мин/ 5	Ср. время ож., Ср. время пр.,
	4 канальная	В порядке поступления	По жребию	Н 5 мин/ 1	Э 10 мин	Э 20 мин	Ср. время ож., Ср. время пр., Вер. отказа
	5 канальная	В порядке поступления	По приоритету (в порядке номеров)	Р 5 мин/ 1		Э 25 мин	Ср. время пр., Вер. отказа
	5 канальная	В порядке поступления	По жребию	Н 2 мин/0,5		Р 10 мин	Ср. время пр., Вер. отказа
	6 канальная	В порядке поступления	Мин.время освобождения	Н 5 мин/ 1	Э 10мин	Э 30мин	Ср. время ож., Ср. время пр., Вер. отказа
	6 канальная	В порядке поступления	Мин.время освобождения	Р 5 мин./0,5	¥	Н 30 мин/ 8	Ср. время ож., Ср. время пр.,
	2 канальная	В порядке поступления	Мин.время освобождения	Р 5 мин./0,5	¥	Н 10 мин/2	Ср. время ож., Ср. время пр.,
	5 канальная	В порядке поступления	По жребию	Э 2 мин/0,5		Н 10 мин	Ср. время пр., Вер. отказа
	1 канальная	В порядке поступления	-	Р 5 мин./0,5	¥	Н 5 мин/ 1	Ср. время ож., Ср. время пр., Вер. отказа
	2 канальная	В порядке поступления	Мин.время освобождения	Э 5мин		Р 10 мин./3	Ср. время пр., Вер. отказа
	3 канальная	В порядке поступления	По приоритету (в порядке номеров)	Н 3 мин/0,5		Р 10 мин	Ср. время пр., Вер. отказа
	4 канальная	В порядке поступления	По жребию	Э 5мин		Р 20 мин./5	Ср. время пр., Вер. отказа
	5 канальная	В порядке поступления	По приоритету (в порядке номеров)	Н 3 мин/0,5	¥	Р 10 мин	Ср. время ож., Ср. время пр.
	6 канальная	В порядке поступления	Мин.время освобождения	Э 5мин		Э 30мин/ 10	Ср. время пр., Вер. отказа
	2 канальная	В порядке поступления	По приоритету (в порядке номеров)	Р 5 мин./0,5	¥	Н 10 мин/2	Ср. время ож., Ср. время пр.,
	1 канальная	В порядке поступления	-	Н 5 мин/ 1	Э 10 мин	Р 5мин	Ср. время ож., Ср. время пр., Вер. отказа
	4 канальная	В порядке поступления	По приоритету (в обратном порядке номеров)	Р 5 мин./0,5	¥	Н 20 мин/ 5	Ср. время ож., Ср. время пр.,
	2 канальная	В порядке поступления	Мин.время освобождения	Р 5 мин./0,5	¥	Н 10 мин/2	Ср. время ож., Ср. время пр.,
	5 канальная	В порядке поступления	По жребию	Э 4 мин/0,5		Н 20 мин	Ср. время пр., Вер. отказа
	1 канальная	В порядке поступления	-	Р 5 мин./0,5	Э 10 мин	Н 5 мин/ 1	Ср. время ож., Ср. время пр., Вер. отказа
	4 канальная	В порядке поступления	По приоритету (в обратном порядке номеров)	Р 5 мин./0,5	¥	Н 20 мин/ 5	Ср. время ож., Ср. время пр.,

5. Лабораторная работа "Моделирование систем массового обслуживания методом особых состояний.".

Цель работы: приобрести практические навыки исследования систем массового обслуживания (СМО) методом имитационного моделирования с использованием метода особых состояний.

5.1. Описание работы.

5.2. Варианты индивидуальных заданий.

Перед выполнением лабораторной работы студентам выдается задание из числа вариантов, приведенных в табл. 5.1.

Законы распределения в табл. 5.1 обозначены следующим образом:

- Э - экспоненциальный;

- Н - нормальный;

- Р - равномерный.

5.3 Порядок выполнения работы.

- Согласно данным варианта составить моделирующий алгоритм для нахождения искомых характеристик СМО.

- Составить программу

- Набрать программу модели СМО на ЭВМ.

- Провести пробный прогон программы при количестве реализаций 10-15 в пошаговом режиме.

- Провести проверку правильности работы программы, при необходимости исправить ошибки и неточности.

- Провести рабочий прогон программы с количеством реализаций 100-200. Первые 10 реализаций выполнить в пошаговом режиме, построить временные диаграммы. Последние реализации выполнить в циклическом режиме. Зафиксировать 10 последних строчек текущих результатов и окончательные результаты моделирования, которые предоставить на проверку преподавателю и сверить с результатами аналитического расчета.

- По указанию преподавателей путем сравнения результатов моделирования СМО, оценить влияние параметров СМО (интенсивность поступления и обслуживания заявок, количества каналов и т.д.) и дать предложения об улучшении этих показателей.

5.4 Содержание отчета

- Индивидуальное задание согласно полученным вариантом.

- Блок-схема моделирующего алгоритма данной СМО.

- Полная распечатка программы с результатами моделирования.

- Анализ полученных результатов.

5.5. Контрольные вопросы.

- Какие методы моделирования СМО существуют?

- Какие характеристики СМО находятся с помощью метода "особых состояний"?

- Что выбрано в качестве единичной реализации в данной модели?

- Как найти аналитически искомую характеристику СМО?

- Особенности моделирования СМО с ограниченным ожиданием.

- Особенности моделирования СМО с выбором заявок по жребию.

- Особенности моделирования ситуаций, возникающих при формировании заявки, которая пришла после высвобождения канала при наличии очереди.

- Анализ результатов моделирования по данной лабораторной работе.

- Ответы на вопросы иллюстрируются примерами из отчета о данной лабораторную работу.

Таблица 5.1 Задания на лабораторную работу по моделированию СМО методом особых состояний

Номер бригады	Тип СМО	Выбор заявок из очереди	Выбор каналов	Интервал поступления	Время ожидания	Время обслуживания	Определить
	4 канальная	В случайном порядке	По жребию	Р 3 мин./0,5	¥	Н 12 мин/ 3	Ср. время ожидания, Ср. время простоя
	1 канальная	В случайном порядке	-	Р 5 мин./1	¥	Н 5 мин/ 1	Ср. время ожидания, Ср. время простоя
	2 канальная	В порядке поступления	Мин.время освобождения	Э 6мин	¥	Р 12 мин./3	Ср. время ожидания, Ср. длину очереди
	6 канальная	В случайном порядке	Мин.время освобождения	Р 5 мин./1,5	¥	Н 30 мин/ 8	Ср. время ожидания, Ср. время простоя
	4 канальная	В порядке поступления	По жребию	Э 5мин	¥	Р 20 мин./5	Ср. время ожидания, Ср. длину очереди
	2 канальная	В случайном порядке	Мин.время освобождения	Р 5 мин./1	¥	Н 10 мин/2	Ср. время ожидания, Ср. время простоя
	1 канальная	В порядке поступления	-	Э 5мин	¥	Р 5 мин./0,5	Ср. время ожидания, Ср. длину очереди
	6 канальная	В порядке поступления	Мин.время освобождения	Э 4мин	¥	Р 24 мин / 5	Ср. время ожидания, Ср. длину очереди
	2 канальная	По минимальному времени отказа	Мин.время освобождения	Н 5 мин/ 1	Э 10 мин	Э 10 мин	Ср. время ожидания, Ср. время простоя
	6 канальная	По минимальному времени отказа	Мин.время освобождения	Н 5 мин/ 1	Э 10мин	Э 30мин	Ср. время ожидания, Ср. время простоя
	4 канальная	По минимальному времени отказа	По жребию	Н 5 мин/ 1	Э 10 мин	Э 20 мин	Ср. время ожидания, Ср. время простоя
	1 канальная	По минимальному времени отказа	-	Н 5 мин/ 1	Э 10 мин	Э 5мин	Ср. время ожидания, Ср. время простоя
	6 канальная	По минимальному времени отказа	Мин.время освобождения	Н 5 мин/ 1	Э 10мин	Э 30мин	Ср. время ожидания, Ср. время простоя
	2 канальная	По минимальному времени отказа	Мин.время освобождения	Н 5 мин/ 1	Э 10 мин	Э 10 мин	Ср. время ожидания, Ср. время простоя
	1 канальная	По минимальному времени отказа	-	Н 5 мин/ 1	Э 10 мин	Э 5мин	Ср. время ожидания, Ср. время простоя
	6 канальная	В порядке поступления	Мин.время освобождения	Э 5мин	¥	Э 30мин	Ср. время ожидания, Ср. длину очереди
	1 канальная	В порядке поступления	-	Э 5мин	¥	Р 5 мин./0,5	Ср. время ожидания, Ср. длину очереди
	4 канальная	В порядке поступления	По жребию	Э 5мин	¥	Р 20 мин./5	Ср. время ожидания, Ср. длину очереди
	2 канальная	В порядке поступления	Мин.время освобождения	Э 5мин	¥	Р 10 мин./3	Ср. время ожидания, Ср. длину очереди
	1 канальная	В случайном порядке	-	Р 5 мин./0,5	¥	Н 5 мин/ 1	Ср. время ожидания, Ср. время простоя
	4 канальная	В случайном порядке	По жребию	Р 5 мин./1,5	¥	Н 20 мин/ 5	Ср. время ожидания, Ср. время простоя
	6 канальная	В случайном порядке	Мин.время освобождения	Р 5 мин./1	¥	Н 30 мин/ 8	Ср. время ожидания, Ср. время простоя
	2 канальная	В случайном порядке	Мин.время освобождения	Р 5 мин./0,5	¥	Н 10 мин/2	Ср. время ожидания, Ср. время простоя
	4 канальная	По минимальному времени отказа	По жребию	Н 5 мин/ 1	Э 10 мин	Э 20 мин	Ср. время ожидания, Ср. время простоя
	2 канальная	В случайном порядке	Мин.время освобождения	Р 5 мин./0,5	¥	Н 10 мин/2	Ср. время ожидания, Ср. время простоя
	6 канальная	В порядке поступления	Мин.время освобождения	Э 5мин	¥	Э 30мин	Ср. время ожидания, Ср. длину очереди
	1 канальная	По минимальному времени отказа	-	Н 5 мин/ 1	Э 10 мин	Э 5мин	Ср. время ожидания, Ср. время простоя
	4 канальная	В случайном порядке	По жребию	Р 6 мин./1,5	¥	Н 24 мин/ 5	Ср. время ожидания, Ср. время простоя
	6 канальная	По минимальному времени отказа	Мин.время освобождения	Н2 мин/ 1	Э 10мин	Э 12мин	Ср. время ожидания, Ср. время простоя
	1 канальная	В порядке поступления	-	Э 5мин	¥	Р 5 мин./1,5	Ср. время ожидания, Ср. длину очереди
	2 канальная	По минимальному времени отказа	Мин.время освобождения	Н 4 мин/ 1	Э 10 мин	Э 8 мин	Ср. время ожидания, Ср. время простоя
	6 канальная	В случайном порядке	Мин.время освобождения	Р 5 мин./0,5	¥	Н 30 мин/ 8	Ср. время ожидания, Ср. время простоя
	4 канальная	По минимальному времени отказа	По жребию	Н 5 мин/ 1	Э 10 мин	Э 20 мин	Ср. время ожидания, Ср. время простоя
	1 канальная	В случайном порядке	-	Р 5 мин./0,5	¥	Н 5 мин/ 1	Ср. время ожидания, Ср. время простоя

Литература:

Основная:

1. Советов Б.Я. Моделирование систем: учебник для вузов / Б. Я. Советов, С. А. Яковлев; Б.Я. Советов, С.А. Яковлев. - 3-е изд., перераб. и доп. - М.: Высшая школа, 2001. - 343с.: ил. - ISBN 5-06-003860-2.

2. Советов Б.Я. Моделирование систем: практикум: учебник для вузов / Б. Я. Советов, С. А. Яковлев; Б.Я. Советов, С.А. Яковлев. - Изд. 3-е, стер. - М.: Высшая школа, 2005. - 295с.: ил. - ISBN 5-06-004087-9.

3. Бусленко Н.П. Моделирование сложных систем / Н. П. Бусленко; Н.П. Бусленко. - 2-е изд., перераб. - М.: Наука, 1978. - 399с.: ил.

Дополнительная:

4. Моделирование систем: учебник для вузов / С. И. Дворецкий [и др.]; С.И. Дворецкий, Ю.Л. Муромцев, В.А. Погонин, А.Г. Схиртладзе. - М.: ИЦ "Академия", 2009. - 320с. - (Высшее профессиональное образование. Машиностроение). - ISBN 978-5-7695-4737-9

5. Колесов Ю.Б. Моделирование систем. Объектно-ориентированный подход: учебное пособие для вузов / Ю. Б. Колесов, Ю. Б. Сениченков; Ю.Б. Колесов, Ю.Б. Сениченков. - СПб.: БХВ-Петербург, 2006. - 192с.: ил. - ISBN 5-94157-579-3

6. Емельянов А.А. Имитационное моделирование экономических процессов: учебное пособие для вузов / А. А. Емельянов, Е. А. Власова, Р. В. Дума; А.А. Емельянов, Е.А. Власова, Р.В. Дума; под ред. А.А. Емельянова. - М.: Финансы и статистика, 2002. - 368с.: ил. - ISBN 5-279-02572-0.

7. Бусленко Н.П. Моделирование сложных систем / Н. П. Бусленко; Н.П. Бусленко. - М.: Наука, 1968. - 355с.: черт.

8. Бусленко Н.П. Метод статистического моделирования / Н. П. Бусленко. - 1970.

Интернет-ресурсы

9. http://a1308.ru/books/id547 (Имитационное моделирование. Классика CS Кельтон В., Лоу А.)

10. ww.sworld.com.ua/konfer32/867.pdf (Имитационное моделирование в экономических исследованиях: современное состояние и технология применения.

12	Поделиться:

Воспользуйтесь поиском по сайту: