 |
Интеграл сходится, поэтому сходится и данный ряд.
|
|
|
|
МАТЕМАТИКА
Часть третья
Учебно-методические указания по изучению дисциплины и выполнению контрольных работ для студентов-заочников второго курса
высшего профессионального образования
Краснодар
УДК
Составители: доцент Терещенко И.В., доцент Братчиков А.В., ассистент Сычева В.Е.
Математика. Учебно – методические указания по изучению дисциплины и выполнению контрольных работ для студентов-заочников специальностей 140211,140101,130503 факультета НГиЭ высшего профессионального образования. – Краснодар 2006. – 25 с.
В учебно-методических указаниях изложены программа дисциплины, варианты контрольных заданий, темы практических занятий, вопросы к зачету (или экзамену), рекомендуемая литература, приведены примеры выполнения и требования к оформлению контрольных работ.
Печатается по решению методического совета Кубанского государственного технологического университета.
Рецензенты: д-р техн. наук, профессор Вартумян Г.Т.
канд. техн. наук, доцент Данович Л.М.
© КубГТУ, 2006
Содержание
Введение ……………………………………………………………………………….….4
1. Инструкция по работе с учебно-методическими указаниями………………….……4
2. Программа дисциплины………………………………………………………….…….5
3. Контрольные работы…………………………………………………………………...6
4. Задания на контрольную работу……………………...……………………………...17
5. Содержание и оформление контрольных работ…………………………………….23
6. Темы практических занятий………………………………………………………….24
7. Вопрос подготовки к экзамену (зачету)………….………………………………….24
8. Список рекомендуемой литературы…………………………………………………25
|
|
|
Введение
Инженер должен в области математики иметь представление:
- о математике как особом способе познания мира, общности ее понятий и
представлений;
- о математическом моделировании;
- об информации, методах ее хранения, разработки и передачи;
знать и уметь использовать:
- основные понятия и методы математического анализа, аналитической геометрии, линейной алгебры, теории функций комплексного переменного, теории вероятностей и математической статистики, дискретной математики;
- математические модели простейших систем и процессов в естествознании и технике;
- вероятностные модели для конкретных процессов и проводить расчеты в рамках построенной модели;
иметь опыт:
- употребления математической символики для выражения количественных и качественных отношений объектов;
- исследования моделей с учетом их иерархической структуры и оценки пределов применимости полученных результатов:
- использования основных приемов обработки экспериментальных данных;
- аналитического и численного решения алгебраических уравнений;
- исследования, аналитического и численного решения обыкновенных дифференциальных уравнений;
- аналитического и численного решения основных уравнений математической физики;
- программирования и использования возможностей вычислительной техники и программного обеспечения;
Цель курса «Математика»:
- дать студентам необходимую математическую подготовку для изучения общенаучных, общеинженерных и специальных дисциплин;
- привить студентам навыки логического и алгоритмического мышления;
- овладеть методами исследования и решения математических и прикладных задач по специальности;
- выработать умения самостоятельно расширять математические знания и применять их при анализе инженерных задач.
Инструкция по работе с учебно–методическими указаниями.
|
|
|
В разделе «Программа дисциплины» приведены темы и указывается, что необходимо знать в пределах каждой темы. В конце тем приводятся вопросы для самопроверки и литература из списка рекомендуемой литературы с указанием глав, страниц, где излагается материал темы.
Пример.
Литература: [3, гл.13 c. 3-9], [4, c. 143-162],
где 2 и 4 – порядковые номера литературных источников из списка рекомендуемой литературы.
Вариант контрольного задания выбирается по последней цифре шифра зачётной книжки. Последняя цифра шифра (0) соответствует 10 варианту в контрольном задании. Например, в 10 варианте выполняют следующие номера из предложенных заданий контрольной работы: 310,320,330 и так далее.
В разделе «Темы практических занятий» приводятся наименования практических занятий, которые будут проводиться в период экзаменационной сессии, и указывается литература для подготовки.
Программа дисциплины.
Тема 6. Кратные, криволинейные и поверхностные интегралы. Векторный анализ.
Двойной интеграл. Вычисление площадей и объемов с помощью двойных интегралов. Замена переменных в двойном интеграле. Тройной интеграл. Вычисление объемов с помощью тройных интегралов. Криволинейный интеграл. Вычисление криволинейного интеграла. Поверхностный интеграл. Вычисление поверхностного интеграла. Формула Стокса. Формула Остроградского. Скалярное и векторное поля. Задача о потоке векторного поля.
Литература: [4 гл. 13, с. 307-368)]
Вопросы для самоконтроля.
1. Вычисление двойного интеграла.
2. Вычисление двойного интеграла в полярных координатах.
3. Вычисление тройного интеграла.
4. Вычисление площадей с помощью с помощью двойных интегралов.
5. Вычисление объемов с помощью тройных интегралов.
6. Вычисление криволинейного интеграла.
7. Вычисление поверхностного интеграла.
Тема 7. Ряды. Применение степенных рядов к приближенному вычислению значений функций, интегралов, решения дифференциальных уравнений.
Числовые ряды. Свойства сходящихся рядов. Необходимое условие сходимости ряда. Знакочередующиеся ряды. Абсолютная и условная сходимость рядов. Степенные ряды. Применение степенных рядов к приближенному вычислению значений функций, интегралов, решения дифференциальных уравнений. Ряды Фурье.
|
|
|
Литература: [4, гл. 14 с. 379-416].
Вопросы для самоконтроля.
1. Исследование сходимости числового ряда.
2. Исследование на абсолютную и условную сходимость знакочередующегося ряда.
3. Нахождение интервала сходимости степенного ряда.
4. Приближенные вычисления значений функции с помощью степенных рядов.
5. Применение степенных рядов к вычислению определенных интегралов.
6. Интегрирование дифференциальных уравнений с помощью рядов.
7. Разложение функций в ряды Фурье.
Контрольные работы.
Программой дисциплины «Математика» для студентов II курса предусмотрено выполнение контрольных работ № 4,5.
3.1. При выполнении контрольной работы № 4 необходимо изучить следующие вопросы: двойной интеграл, вычисление площадей и объемов с помощью двойных интегралов, замена переменных в двойном интеграле, тройной интеграл, вычисление объемов с помощью тройных интегралов, криволинейный интеграл, вычисление криволинейного интеграла, вычисление поверхностного интеграла, формула Стокса, Остроградского; скалярное и векторное поля, задача о потоке векторного поля.
Ниже приведены примеры выполнения расчетов.
К заданиям 331-340.
Пример. Вычислить двойной интеграл по области, ограниченной линиями
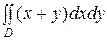 D: y=-x2 +1, x=0, y=0.
D: y=-x2 +1, x=0, y=0.
Решение. Построим область D. График функции y=-x2 +1 представляет собой параболу с вершиной в точке (0;1), симметричную относительно оси OY; x=0 – прямая, совпадающая с осью OY; y=0 - прямая, совпадающая с осью OX
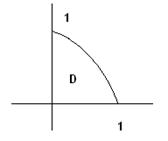
Для вычисления двойного интеграла воспользуемся формулой


Область интегрирования D ограничена слева и справа прямыми х=0, х=1, снизу y=0 и сверху
y=-x2+1


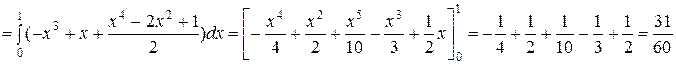 Ответ:
Ответ: 
К заданиям 341-350. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнениями в декартовых координатах (а>0)

Решение: Преобразуем уравнение кривой к полярным координатам
Положим 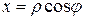 ,
, 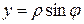
В результате получим
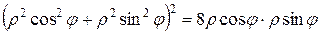
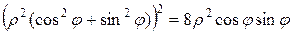

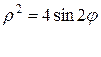
 Очевидно, что изменению полярного угла
Очевидно, что изменению полярного угла 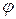 от 0 до
от 0 до 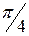 соответствует четверть искомой площади. Изобразим полученную кривую на чертеже.
соответствует четверть искомой площади. Изобразим полученную кривую на чертеже.
|
|
|
Следовательно, 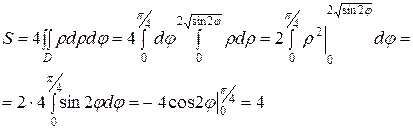
Ответ: 4
К заданиям 351-360.
Пример.Вычислить с помощью тройного интеграла объем тела, ограниченного поверхностями  ,
, 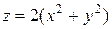 ,
,  ,
,  . Сделать чертеж данного тела и его проекции на плоскость XOY
. Сделать чертеж данного тела и его проекции на плоскость XOY
Решение.

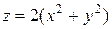 - параболоиды вращения
- параболоиды вращения

 - цилиндрические поверхности
- цилиндрические поверхности
Наше тело представляет собой «параболический башмачок», который вырезают цилиндрические поверхности  и
и 
 между параболоидами вращения. Снизу «башмачок» ограничен куском поверхности
между параболоидами вращения. Снизу «башмачок» ограничен куском поверхности 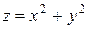 , а сверху куском поверхности параболоида вращения
, а сверху куском поверхности параболоида вращения
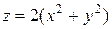
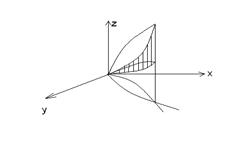 Проекция этого тела на плоскость XOY дает множество, состоящее из точек (x,y), координаты которых удовлетворяют неравенствам
Проекция этого тела на плоскость XOY дает множество, состоящее из точек (x,y), координаты которых удовлетворяют неравенствам 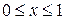


Поэтому, 

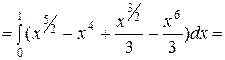 (
( -
- 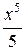 +
+  -
- 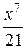 )=
)= 

Ответ: 
К заданиям 361-370.
Пример 1. Вычислить криволинейный интеграл 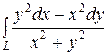 вдоль дуги окружности x=cost, y=sint, обходя ее против хода часовой стрелки от точки А(1;0) до точки В(0;1). Сделать чертеж.
вдоль дуги окружности x=cost, y=sint, обходя ее против хода часовой стрелки от точки А(1;0) до точки В(0;1). Сделать чертеж.
Решение. L – дуга окружности x=cost y=sint, R=1. Изобразим на чертеже дугу окружности по  которой вычисляем интеграл.
которой вычисляем интеграл.
Так как кривая задана в параметрическом виде x=x(t) y=y(t) (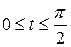 ), то криволинейный интеграл II рода сводится к определенному интегралу по формуле
), то криволинейный интеграл II рода сводится к определенному интегралу по формуле 
Найдем 
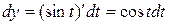
Тогда 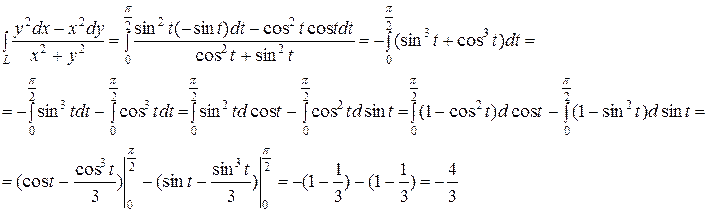 Ответ:
Ответ: 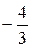
Пример 2. Вычислить криволинейный интеграл 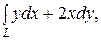 если L – контур треугольника с вершинами А(1;2), В(3;1), С(2;5) пробегаемый против хода часовой стрелки.
если L – контур треугольника с вершинами А(1;2), В(3;1), С(2;5) пробегаемый против хода часовой стрелки.
Решение.Составим уравнение прямых АВ, ВС, СА и изобразим контур интегрирования на чертеже.
АВ: 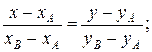
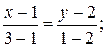
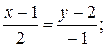

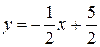

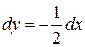
ВС: 
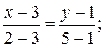

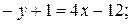
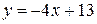

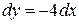
СA: 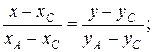
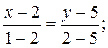
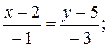



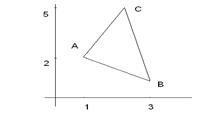
Следовательно,



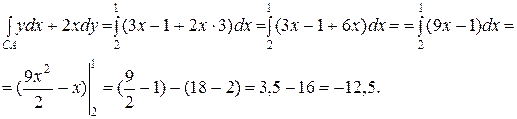
Получаем, 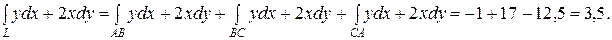
Ответ: 3,5
К заданиям 371-380.
Пример. Даны векторное поле 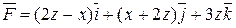 и плоскость x+4y+z-4=0 (p), которая совместно с координатными плоскостями образует пирамиду V.
и плоскость x+4y+z-4=0 (p), которая совместно с координатными плоскостями образует пирамиду V.
Пусть 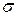 - основание пирамиды, принадлежащее плоскости (р);
- основание пирамиды, принадлежащее плоскости (р); 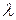 - контур, ограничивающий
- контур, ограничивающий 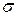 ;
;
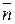 –нормаль к
–нормаль к 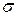 , направленная вне пирамиды V.
, направленная вне пирамиды V.
Требуется вычислить:
1) поток векторного поля  через поверхность
через поверхность 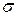 в направлении нормали
в направлении нормали 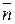 ;
;
2) циркуляцию векторного поля  по замкнутому контуру
по замкнутому контуру 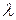 и ограниченной им замкнутой поверхности
и ограниченной им замкнутой поверхности 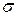 с нормалью;
с нормалью;
3) поток векторного поля  через полную поверхность пирамиды V в направлении внешней нормали к ее поверхности, применив теорему Остроградского.
через полную поверхность пирамиды V в направлении внешней нормали к ее поверхности, применив теорему Остроградского.
Решение:
1) Поток векторного поля  через поверхность S в сторону, определяемую единичным вектором нормали
через поверхность S в сторону, определяемую единичным вектором нормали 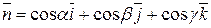 к поверхности S, вычисляется по формуле
к поверхности S, вычисляется по формуле
П= 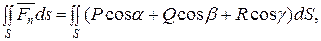 где
где 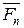 -скалярное произведение вектора поля и единичного вектора, выбранного направления, а
-скалярное произведение вектора поля и единичного вектора, выбранного направления, а 
Для данного векторного поля 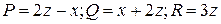 и по определению потока получаем
и по определению потока получаем
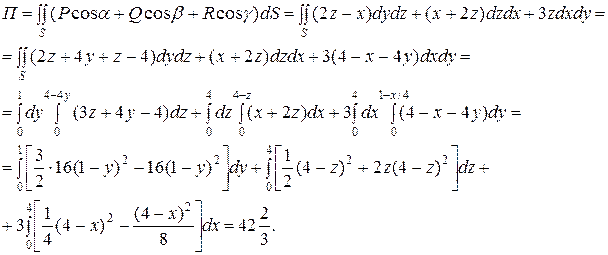
Ответ: 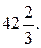
2) циркуляцию векторного поля  по замкнутому контуру
по замкнутому контуру 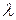 и ограниченной им замкнутой поверхности
и ограниченной им замкнутой поверхности 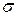 с нормалью вычисляем по формуле Стокса Ц=
с нормалью вычисляем по формуле Стокса Ц=  , где С – контур
, где С – контур 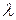 , проходящей через три данные точки,
, проходящей через три данные точки, 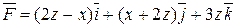 . Замкнутый контур
. Замкнутый контур 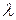 представляет собой треугольник с вершинами М(4;0;0), N(0;1;0), P(0;0;4)
представляет собой треугольник с вершинами М(4;0;0), N(0;1;0), P(0;0;4)
|
|
|
Найдем ротор данного векторного поля.

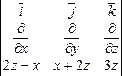 =
= 
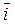 -
- 

+ 
Следовательно, 
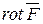 dS=
dS= 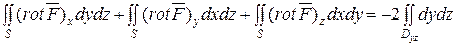 +
+ 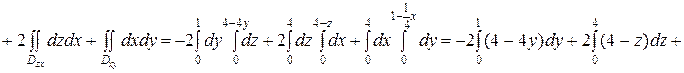

Ответ: 14.
3) Для вычисления потока векторного поля  через полную поверхность пирамиды V в направлении внешней нормали к ее поверхности применим формулу Остроградского
через полную поверхность пирамиды V в направлении внешней нормали к ее поверхности применим формулу Остроградского 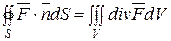 .
.
Согласно определению, имеем 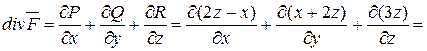
 .
.
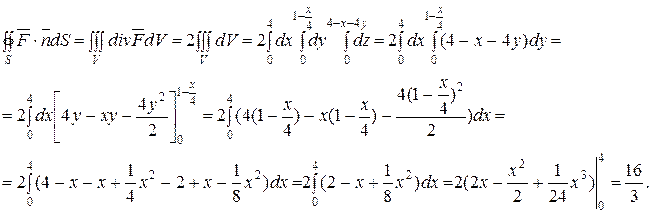
Ответ: 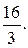
К заданиям 381-390.
Пример.
Проверить является ли векторное поле 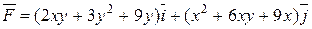
потенциальным и соленоидальным. В случае потенциальности поля  найти его потенциал.
найти его потенциал.
Решение. Векторное поле  (М) называется потенциальным, если rot
(М) называется потенциальным, если rot  =0. Вычислим rot
=0. Вычислим rot  .
.


 =
= 
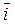 - -
- - 
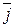 +
+ 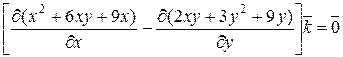
Следовательно, данное векторное поле является потенциальным.
Потенциал u=u(x,y) вычислим по формуле
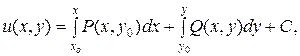
то есть, 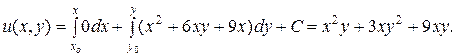 Здесь в качестве начальной точки взята точка М0(0;0).
Здесь в качестве начальной точки взята точка М0(0;0).
Векторное поле  (М) называется соленоидальным, если div
(М) называется соленоидальным, если div  =0.
=0.
Вычислим div  .
.
Согласно определению, имеем 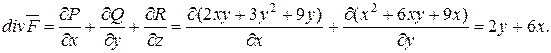
Ответ: поле является потенциальным, 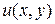 =
= 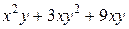 ;
;
поле не является соленоидальным.
3.2. При выполнении контрольной работы № 5 необходимо изучить следующие вопросы: исследование сходимости числового ряда, исследование на абсолютную и условную сходимость знакочередующегося ряда, нахождение интервала сходимости степенного ряда, приближенные вычисления значений функции с помощью степенных рядов, применение степенных рядов к вычислению определенных интегралов, интегрирование дифференциальных уравнений с помощью рядов, разложение функций в ряды Фурье.
Ниже приведены примеры выполнения расчетов.
К заданиям 391-400.
Пример. Исследовать сходимость числового ряда 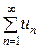 ,
,
где а) 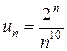 ; б)
; б)  .
.
Решение. а) Для исследования сходимости числового ряда  применим признак Даламбера; имеем
применим признак Даламбера; имеем  ,
, 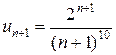 ,
, 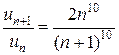 , значит,
, значит,
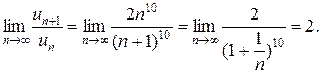 Так как 2>1, ряд расходится.
Так как 2>1, ряд расходится.
Ответ: ряд расходится.
б) Для исследования сходимости числового ряда 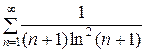 применим интегральный признак:
применим интегральный признак: 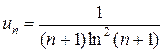 ,
, 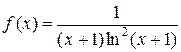 ,
,
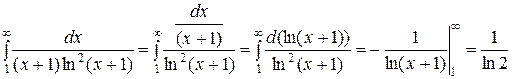
Интеграл сходится, поэтому сходится и данный ряд.
Ответ: ряд сходится.
К заданиям 401-410.
Пример. Найти интервал сходимости степенного ряда  , где
, где 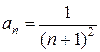

Решение: 
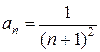 ,
, 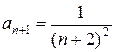 ,
,

 следовательно, ряд сходится для значений
следовательно, ряд сходится для значений 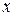 , удовлетворяющих неравенству -1<
, удовлетворяющих неравенству -1< 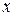 <1. Исследуем сходимость ряда на концах промежутка. Если
<1. Исследуем сходимость ряда на концах промежутка. Если 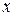 =1, то получим обобщенный гармонический ряд
=1, то получим обобщенный гармонический ряд  , который сходится, так как 2>1.
, который сходится, так как 2>1.
Если 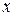 =-1, то получим знакопеременный ряд
=-1, то получим знакопеременный ряд 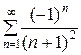 , который сходится, так как удовлетворяет условиям признака Лейбница.
, который сходится, так как удовлетворяет условиям признака Лейбница.
К заданиям 411-420.
Пример. Вычислить значение функции 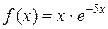 при
при 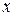 = 0,2 точностью до 0,001, разложив ее в степенной ряд.
= 0,2 точностью до 0,001, разложив ее в степенной ряд.
Решение. Разложение функции 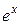 имеет вид
имеет вид 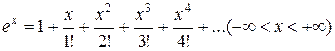 . Заменим
. Заменим 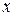 на
на  ; получим
; получим

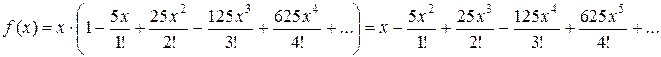 Следовательно, при
Следовательно, при 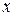 = 0,2
= 0,2
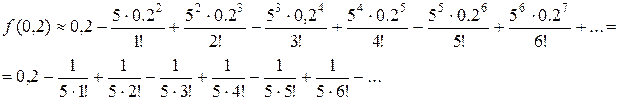
Так как знакопеременный ряд удовлетворяет условиям признака Лейбница, допускаемая погрешность по абсолютной величине должна быть меньше первого из отброшенных членов ряда. Нетрудно видеть, что 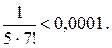 Произведя вычисления, в результате получаем
Произведя вычисления, в результате получаем
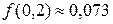
Ответ: 0,073.
К заданиям 421-430.
Пример. Вычислить определенный интеграл 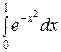 с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и проинтегрировав его почленно.
с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и проинтегрировав его почленно.
Решение. 
Ответ: 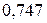
К заданиям 431-440.
Пример. Найти четыре первых, отличных от нуля члена разложения в степенной ряд решения y=y(x) дифференциального уравнения 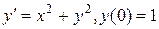 .
.
Решение. В тех случаях, когда для уравнения 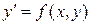 требуется решить задачу Коши при начальном условии y(x0)=y0, решение можно искать с помощью ряда Тейлора:
требуется решить задачу Коши при начальном условии y(x0)=y0, решение можно искать с помощью ряда Тейлора: 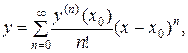 где
где 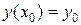 ,
, 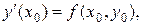 а дальнейшие производные находят последовательным дифференцированием исходного уравнения и подстановкой в результат дифференцирования вместо
а дальнейшие производные находят последовательным дифференцированием исходного уравнения и подстановкой в результат дифференцирования вместо 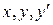 , … значений
, … значений 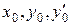 и всех остальных найденных последующих производных.
и всех остальных найденных последующих производных.
Из уравнения и начального условия находим  Дифференцируя данное уравнение, последовательно получаем
Дифференцируя данное уравнение, последовательно получаем  ,
, 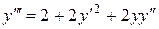 .Полагая
.Полагая  , и используя
, и используя 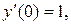 находим
находим 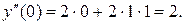 Аналогично, используя значения
Аналогично, используя значения
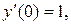
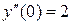 , находим
, находим 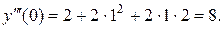
Искомое решение имеет вид 
Ответ: 
К заданиям 441-450.
Пример. Разложите функцию 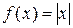 в ряд Фурье в интервале
в ряд Фурье в интервале  .
.
Решение. Эта функция – кусочно - монотонная и ограниченная. Следовательно, она допускает разложение в ряд Фурье.
Определим ее коэффициенты Фурье:
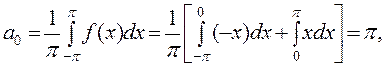
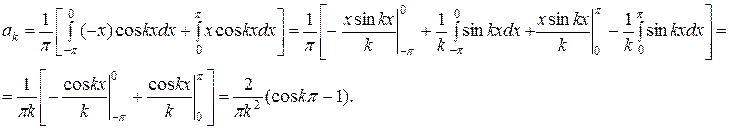
 при k – четном,
при k – четном,  при k – нечетном.
при k – нечетном.

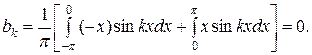
Таким образом, получаем ряд 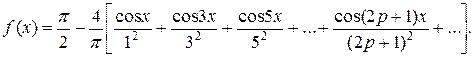
Этот ряд сходится во всех точках, и его сумма равна данной функции.
Ответ: 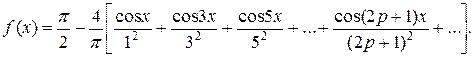
|
|
|
12 |


