 |
Методы статистической обработки экспериментальных данных
|
|
|
|
В современных исследованиях по проблемам педагогики широко используются методы математической обработки данных. К методам обработки количественных данных относятся статистические приемы подведения итогов исследования, выявления определенных связей между ними, проверки достоверности выдвинутой гипотезы.
Математическая обработка результатов исследования обеспечивает их доказательность, репрезентативность. В сочетании с качественными показателями количественная обработка данных значительно повышает объективность исследования. Статистическая обработка результатов, регистрирующая изучение отдельных явлений позволяет сделать обобщения и выводы относительно всей совокупности изучаемых явлений. Важной особенностью использования статистических методов в педагогических исследованиях состоит в том, что это позволяет применять количественное изучение даже там, где невозможно определить сами свойства изучаемых объектов. Например, невозможно прямо измерить уровень развития нравственных качеств обучаемых, степень эффективности конкретного метода обучения и пр. Но, регистрируя соответствующие события, поступки, проявления, можно получить определенные качественные характеристики всех этих признаков, определить возможные закономерности их проявления, подтвердить правильность высказанных гипотез.
В статистике проверка гипотез осуществляется с помощью критериев статической оценки различий. Статистический критерий – это решающее правило, обеспечивающее надежное поведение, т.е. принятие истинной и отклонение ложной гипотезы с высокой вероятностью (Г.В.Суходольский). Статистические критерии обозначают также метод расчета определенного числа и само это число.
|
|
|
Статистические критерии, применяемые в педагогике, делятся на параметрические и непараметрические. К параметрическим относятся критерии, включающие в формулу расчета параметры распределения, т.е. среднее и дисперсии (критерии Стьюдента, Фишера, Хи-квадрат). К непараметрическим относят критерии, основанные на оперировании частотами или рангами и не включающие в формулу расчета параметров распределения (критерии знаков, Колмогорова-Смирнова, Уилкоксона, Манна-Уитни). Обе группы критериев имеют свои преимущества и недостатки. Сравнительная характеристика возможностей и ограничений параметрических и непараметрических критериев дана в следующей таблице.
| Параметрические критерии | Непараметрические критерии |
| Позволяют прямо оценить различия в средних, полученных в двух выборках (критерий Стьюдента) | Позволяют оценить лишь средние тенденции (напр., ответить на вопрос, чаще ли в выборке А встречаются более высокие, а в выборке Б – более низкие значения признака (критерии Q,U и др.) |
| Позволяют прямо оценить различия в дисперсиях (критерий Фишера) | Позволяют оценить лишь различия в диапазонах вариативности признака |
| Позволяют выявить тенденции изменения признака при переходе от условия к условию (дисперсионный однофакторный анализ), но лишь при условии нормального распределения признака | Позволяют выявить тенденции изменения признака при переходе от условия к условию при любом распределении признака (критерии тенденций L и S) |
| Позволяют оценить взаимодействие двух и более факторов в их влиянии на изменения признака (двухфакторный дисперсионный анализ) | Эта возможность отсутствует |
| Экспериментальные данные должны отвечать двум, а иногда трем условиям: а) значения признака измерены по интервальной шкале; б)распределение признака является нормальным; в)в дисперсионном анализе должно соблюдаться требование равенства дисперсий в ячейках комплекса | Экспериментальные данные могут не отвечать ни одному из условий: а) значения признака могут быть представлены в любой шкале, начиная от шкалы наименований; б)распределение признака может быть любым и совпадение его с каким-либо теоретическим законом распределения необязательно и не нуждается в проверке; в)требование равенства дисперсий отсутствует |
| При выполнении указанных условий параметрические критерии являются более мощными по сравнению с непараметрическими критериями | При несоблюдении указанных условий непараметрические критерии более надежны, т.к. они менее чувствительны к «засорениям» |
| Математические расчеты довольно сложны | Математические расчеты большей частью просты и занимают мало времени |
|
|
|
Параметрические методы
Критерий Стьюдента
Для сравнения выборочных средних величин, принадлежащих к двум совокупностям данных, и для решения вопроса о том, отличаются ли средние значения статистически достоверно друг от друга в психолого-педагогических экспериментах часто используют t -критерий Стьюдента, расчетное значение которого определяется по формуле:
,
где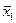 
‑ среднее выборочное значение переменной по одной выборке данных; 
‑среднее выборочное значение по другой выборке данных; m1 и m2 ‑ интегрированные показатели отклонений частных значений из двух выборок от соответствующих их средних величин.
Если t расч больше или равно табличному, то делают вывод о том, что сравниваемые средние значения из двух выборок действительно статистически достоверно различаются с вероятностью допустимой ошибки.
Такая методика применяется тогда, когда необходимо установить, удался или не удался эксперимент, оказал или не оказал он влияние на уровень того качества, для изменения которого он предназначался.
Если t расчетное меньше t табличного, то в этом случае нет убедительных оснований для того, что эксперимент удался, даже если сами средние величины в начале и в конце эксперимента по своим абсолютным значениям различны.
Критерий φ* — угловое преобразование Фишера
Данный метод описан во многих руководствах (Плохинский Н.А., 1970; Гублер Е.В., 1978; Ивантер Э.В., Коросов А.В., 1992 и др.) Настоящее описание опирается на тот вариант метода, который был разработан и изложен Е.В. Гублером.
|
|
|
Критерий Фишера предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта. Критерий оценивает достоверность различий между процентными долями двух выборок, в которых зарегистрирован интересующий исследователя эффект.
Суть углового преобразования Фишера состоит в переводе процентных долей в величины центрального угла, который измеряется в радианах. Большей процентной доле будет соответствовать больший угол φ, а меньшей доле - меньший угол, но соотношения здесь не линейные:
φ = 2·arcsin(
),
где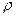 
- процентная доля, выраженная в долях единицы.
При увеличении расхождения между углами φ1 и φ2 и увеличения численности выборок значение критерия возрастает. Чем больше величина φ*, тем более вероятно, что различия достоверны.
|
|
|
