 |
Дифференциальное исчисление
|
|
|
|
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
По выполнению домашней контрольной работы
По дисциплине «математика»
Для студентов заочного отделения
Иркутск 2016
Аннотация
Пособие предназначено для оказания помощи студентам заочного отделения при выполнении домашней контрольной работы по математике Пособие включает в себя некоторые разделы, имеющиеся в этих курсах.
Содержание
1. Теория пределов.
2. Линейная алгебра.
3. Дифференциальное исчисление.
4. Интегральное исчисление.
5. Элементы дискретной математики.
6. Комплексные числа.
7. Элементы теории вероятностей.
8. Литература.
Теория пределов
Изучить по учебной литературе вопросы:
1. Определение предела функции.
2. Свойства пределов функций.
3. Вычисление пределов функций при наличии неопределенности типа 0/0.
4. Вычисление пределов функций, являющихся неопределенностями типа ¥/¥.
5. Понятие разрыва функции. Типы разрывов.
6. Асимптоты графиков функций, их виды и уравнения.
7. Первый и второй замечательные пределы.
Примеры решения задач
1. Вычислить пределы функций:
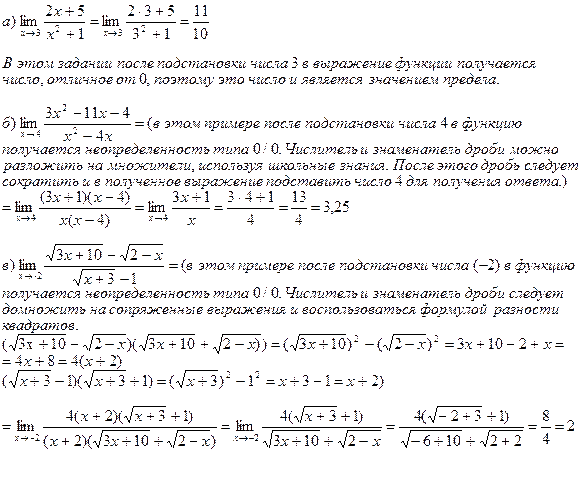
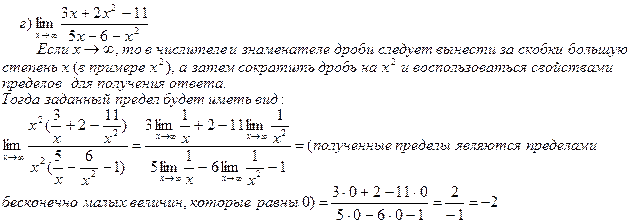
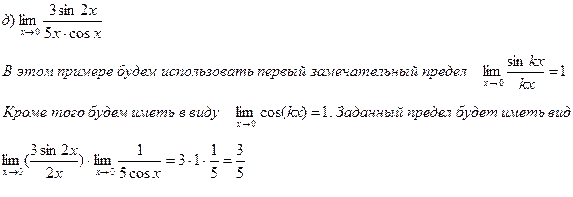
2. Составить уравнения асимптот к графику функции:
Решение
а) Графики функций могут иметь асимптоты трех видов: горизонтальные, вертикальные и наклонные.
Для определения горизонтальной асимптоты следует вычислить предел функции при условии, что х®¥. Если такой предел существует, то график функции имеет горизонтальную асимптоту.
В примере 
График функции имеет горизонтальную асимптоту с уравнением у=2.
Для определения вертикальной асимптоты следует определить значения, при которых функция не существует и найти левые и правые пределы функции. Если хотя бы один из пределов бесконечен, то имеется вертикальная асимптота.
|
|
|
В примере функция не существует при х=3.
Так как оба предела бесконечны, то имеется
вертикальная асимптота с уравнением х=3.
Для определения наклонной асимптоты с уравнением y=kx +b находят
Если первый предел не существует или равен 0, то нет наклонной асимптоты.
В примере 
Так как k=0, то наклонной асимптоты не имеется.
б) 
Выполним последовательно значения пределов:
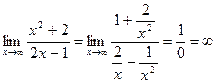График функции не имеет горизонтальной асимптоты.
Функция не существует при х=0,5
График функции имеет вертикальную асимптоту
с уравнением х=0,5
Вычислим 
График функции имеет наклонную асимптоту. 
Наклонная асимптота имеет уравнение у=0,5х + 0,25
3. Построить график функции, определив тип точек разрыва:
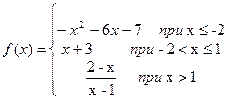
Для заданной функции точками разрыва являются значения аргумента (-2) и 1.
Найдем левые и правые предельные значения функции для этих значений аргумента.
Для построения графика функции с учетом определения типов точек разрыва, потребуется вычисление значений функции в некоторых промежуточных точках
а) x < -2 y=-x2-6x-7 (парабола)
| xi | -5 | -4 | -3 | -2 |
| yi | -2 |
б) -2<x < 1 y=x+3 (прямая)
| xi | -2 | |
| yi |
в) х>1 
| xi | 1,1 | 1,5 | |||
| yi | -0,75 | -0,875 |
Если вычислить 
, то получим уравнение горизонтальной
асимптоты у=-1
Линейная алгебра
Изучить по учебной литературе вопросы:
1. Матрицы, их виды.
2. Действия над матрицами.
3. Определитель матрицы. Вычисление определителей второго и третьего порядков.
4. Обратная матрица, ее определение и получение обратной матрицы второго и третьего порядков.
5. Решение матричных уравнений.
6. Решение системы линейных уравнений по формулам Крамера, в виде матричного уравнения.
Примеры решения задач.
!. Выполнить действия над матрицами 
Составить матрицу М=(2А – В)(В+Е)
|
|
|
Решение
Составим матрицу 2А – В, для чего все элементы матрицы А умножим на 2, а затем из каждого элемента матрицы 2А вычтем соответствующий элемент матрицы В.
Составим матрицу В+Е, где матрица Е является единичной матрицей третьего порядка:
Матрица М является произведением полученных матриц, то-есть каждый ее элемент равен сумме произведений соответствующих элементов строки матрицы 2А-В и столбца матрицы В+Е
2. Вычислить определитель матрицы:
а) 
Решение
а) Для вычисления определителя второго порядка воспользуемся правилом, изложенным в учебной литературе:
б) Для вычисления определителя третьего порядка воспользуемся одним из правил, называемым разложением по элементам первой строки:
3. Найти обратную матрицу для матрицы второго порядка 
Решение
Для получения обратной матрицы А-1 воспользуемся формулой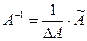 
, где
Для проверки можно найти произведение матриц А и А-1; должна получиться единичная матрица второго порядка.
4. Решить систему уравнений по формулам Крамера 
Решение
Для решения задачи нужно вычислить четыре определителя третьего порядка:
· главный определитель, составленный из коэффициентов при неизвестных;
· дополнительный для х, полученный из главного определителя заменой чисел первого столбца на свободные члены;
· дополнительный для у, полученный из главного определителя заменой чисел второго столбца на свободные члены;
· дополнительный для z, полученный из главного определителя заменой чисел третьего столбца на свободные члены;
Для получения значений неизвестных требуется разделить значения дополнительных определителей на главный определитель.
Решение задачи можно проверить при помощи найденных значений в уравнения системы.
Дифференциальное исчисление
Изучить по учебной литературе вопросы:
1. Производная функция: определение, свойства, таблица производных. 
2. Исследование функции на монотонность.
3. Исследование функции на выпуклость (вогнутость) и точки перегиба.
4. Исследование функции на экстремум.
5. Геометрический и механический смыслы производной.
6. Построение графика функции, используя схему исследования свойств.
|
|
|
Примеры решения задач
1. Найти производные функций:
Решение
При выполнении дифференцирования будем использовать свойства производных, таблицу производных, правило дифференцирования сложных функций.
2. Выполнить исследование свойств функции по первой и второй производным и построить график функции f(x)=x3 - 3x2 - 45x + 20
Решение
Воспользуемся некоторыми пунктами исследования функции:
1)Областью определения этой функции является множество всех действительных чисел. Эта функция не является четной или нечетной. График этой функции не имеет асимптот.
2) Найдем первую производную и определим соответствующие свойства
функции. f’(x)=3x2 – 6x –45. Решим уравнение 3х2 – 6х – 45 = 0. Корнями уравнения являются числа (-3) и 5.
Воспользуемся таблицей:
| х | (-¥; -3) | -3 | (-3;5) | (5;¥) | |
| f’(x) | + | - | + | ||
| f(x) | 
| max | 
| min | 
|
Функция возрастает в интервалах (-¥;-3) и (5;¥), убывает в интервале (-3; 5).
Функция имеет максимальное значение f(-3)=101, имеет минимальное значение f(5)= - 155.
3) Найдем вторую производную f”(x)=(3x2 – 6x –45)’=6x-6.
Решим уравнение 6х-6=0. Решением уравнения является х=1.
Для определения свойств функции воспользуемся таблицей:
| х | (-¥; 1) | (1;¥) | |
| f”(x) | - | + | |
| f(x) | Ç выпуклая | точка перегиба | È вогнутая |
4) Для построения графика функции воспользуемся результатами вычислений, оформленными в виде таблицы:
| х | - 6 | -5 | -3 | - 1 | |||||||
| f(x) | - 34 | - 27 | -74 | -144 | -155 | -99 | |||||
| max | пер. | min |
Интегральное исчисление
Изучить по учебной литературе вопросы:
1. Неопределенный интеграл: определение, свойства, таблица интегралов.
2. Способы вычисления неопределенного интеграла: непосредственное интегрирование, способ подстановки.
3. Определенный интеграл: определение, свойства, геометрический смысл.
4. Способы вычисления определенного интеграла.
5. Применение определенного интеграла к решению практических задач: вычисление площадей плоских фигур.
|
|
|
Примеры решения задач
1) Найти неопределенные интегралы:
Решение
При решении примеров следует пользоваться свойствами неопределенных интегралов, таблицей интегралов, в которую включена формула интеграла функции линейного аргумента, непосредственным интегрированием и методом подстановки.
б) Выполнив почленное деление в подынтегральной функции, получим:
в)
г) Будем использовать подстановку:
д) Воспользуемся подстановкой:
2) Вычислить определенные интегралы:
Решение
При вычислении определенных интегралов используем формулу Ньютона-Лейбница
. Получение первообразной функции F(x) будем выполнять или непосредственно или способом подстановки.
б)
3. Найти площадь фигуры, ограниченной линиями: у=1 – х2 + 4х и 2х – у – 2 =0
Для определения точек пересечения линий составим уравнение из равенства выражений этих линий: 1 – х2 + 4х = 2х – 2; получим уравнение: х2 – 2х – 3 = 0.
Корнями этого уравнения являются числа: (-1) и 3. Для построения линий найдем
значения функций и составим их таблицы:
| х | -1 | х | -1 | ||||||
| у1 | -4 | у2 | -4 |
Построив фигуру на плоскости, вычислим ее площадь, определив значение интеграла
Дискретная математика
Изучить по учебной литературе вопросы:
1. Множества, их виды, способы задания.
2. Простейшие действия над множествами.
3. Отношения, их некоторые виды.
4. Графы, их основные элементы.
5. Некоторые виды графов.
Упражнения и их решение.
1) Составить объединение, пересечение и разность двух множеств.
а) А={3; 4; 6; 7}, B={2; 3; 4; 5}
AÈB={2; 3; 4; 5; 6; 7}, AÇB={3; 4}, A \ B ={6; 7}
б) А=(-1; 3]; B=[1; 5]
AÈB=(-1;5]; AÇB=[1; 3]; A \ B=(-1; 1)
В этом упражнении решение следует сопровождать рисунками.
Комплексные числа
Изучить по учебной литературе вопросы:
1. Определение комплексного числа в алгебраической форме.
2. Геометрическое изображение комплексного числа.
3. Тригонометрическая форма комплексного числа.
4. Выполнение арифметических действий над комплексными числами в алгебраической и тригонометрической формах.
Примеры решения задач
1) Построить на координатной плоскости числа Z1, Z2, где Z1=3-2i, Z2=-1+i.
Решение
На координатной плоскости изобразим точки (3; -2), (-1; 1) и соединим их с началом
координат, получив векторы, конечными точками которых являются заданные точки.
2) Выполнить действия сложения, вычитания, умножения, деления над комплексными числами в алгебраической форме.
|
|
|
Z1=3+4i, Z2=2i18-5i15
Решение
Предварительно преобразуем второе число, используя значения степеней мнимой единицы. i18=i16+2=i16i2=1i2=-1, i15=i12+3=i12i3=i3=-i, Z2=-2+5i
Выполним действия над числами:
Z1+Z2=(3+4i)+(-2+5i)=3+4i-2+5i=(3-2)+(4i+5i)=1+9i
Z1-Z2=(3+4i)-(-2+5i)=3+4i+2-5i=(3+2)+(4i-5i)=5-I
Z1 .Z2=(3+4i) . (-2+5i)=-6+15i – 8i +20i2=-6+7i – 20= - 26 + 7i
3) Представить число в тригонометрической форме Z= 
Найдем модуль и аргумент комплексного числа
|
|
|
