 |
Элементы теории вероятностей
|
|
|
|
Изучить по учебной литературе вопросы:
1. Случайные события, их виды.
2. Вероятность случайного события, способы ее получения.
3. Комбинаторика. Применение элементов комбинаторики к вычислению вероятности.
4. Действия над случайными событиями, вычисление вероятностей результатов действий.
5. Случайные величины, их виды. Закон распределения случайной величины
6. Ряд и функция распределения дискретной случайной величины.
7. Математическое ожидание дискретной случайной величины.
8. Дисперсия дискретной случайной величины.
Примеры решения задач
1) Имеется набор разноцветных шариков, среди которых 5 синих, 3 красных и 2 зеленых. Наугад извлекают 4 шарика. Найти вероятность того, что среди извлеченных шариков 2 синих, 1 красный и 1 зеленый.
Решение
Для определения вероятности случайного события будем использовать классическую формулу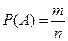 
, в которой n – число всех возможных исходов, m- число исходов, благоприятных появлению события. В задаче значения этих величин следует находить при помощи сочетаний.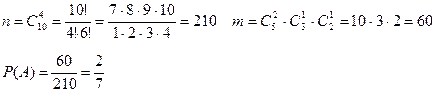 
2) Из карточек разрезной азбуки составлено слово «панорама». Карточки перемешали и наудачу по одной извлекают 5 карточек, выкладывая их в порядке извлечения. Найти вероятность того, что окажется составленным слово «роман».
Решение
В этой задаче можно воспользоваться произведением зависимых случайных событий
А – получение слова «роман»; В1 – извлечение первой карточки с буквой «р»;
В2 – извлечение второй карточки с буквой «о»; и т.д. Тогда А=В1 . В2 . В3 . В4 . В5
Р(А)=Р(В1) . Р(В2) . Р(В3) . Р(В4) . Р(В5)=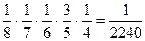 
3) В трех ящиках имеется по 6 одинаковых изделий, среди которых соответственно 2,
1, 3 бракованных. Наугад из каждого ящика извлекают по одному изделию. Найти вероятность того, что среди них окажутся два качественных и одно бракованное изделия.
|
|
|
Решение
Для решения задачи рассмотрим события: А – извлечение двух качественных и одного бракованного изделий, В1 – извлечение качественного изделия из первого ящика;
В2 – извлечение качественного изделия из второго ящика; В3– извлечение качественного изделия из третьего ящика; извлечение бракованного изделия для каждого ящика является событиями 
Составим событие А и вычислим его вероятность
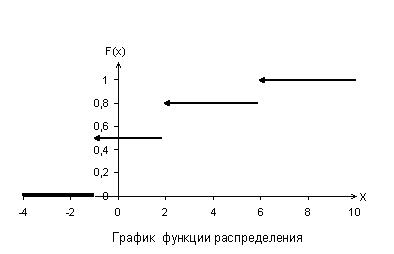
4) Вычислить математическое ожидание и дисперсию случайной величины, составить функцию распределения, начертить многоугольник распределения и график функции распределения. Имеется заданный ряд распределения дискретной случайной величины
| хi | -1 | ||
| pi | 0,5 | 0,3 | 0,2 |
Для вычисления математического ожидания воспользуемся формулой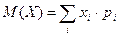 
Получим M(X)=(-1).0,5+2.0,3+6.0,2=1,3
Для вычисления дисперсии воспользуемся двумя соотношениями, одно из которых соответствует определению дисперсии, другое – ее свойству.
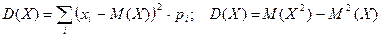
В примере получим: D(X)=(-1-1,3)2 . 0,5+(2-1,3)2 . 0,3+(6-1,3)2 . 0,2=7,21
M(X2)=(-1)2 . 0,5+22 . 0,3+62 . 0,2=8,9
D(X)= 8,9 – 1,32 =7,21 (значения должны совпадать)
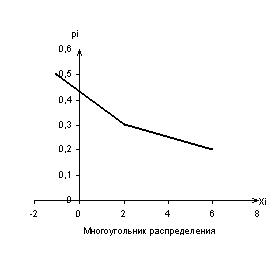
Для построения многоугольника распределения нужно на координатной плоскости построить точки (xi;pi) и последовательно их соединить отрезками.
Для построения функции распределения воспользуемся схемой:
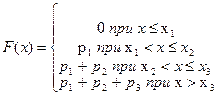
В примере получим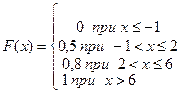 
Используя значения заданного примера получим графики:
Литература
1. Математика: учебник. И.Д. Пехлецкий – М.: Издательский центр Академия, 2007
2. «Общий курс высш. математики» под ред. Ермакова Е.И. М., ИНФРА-М,2004
3. Математика: учебник для студ. сред. проф. учреждений; С.Г. Григорьев, С.В. Иволгина; - М.: Издательский центр «Академия», 2010
4. Теория вероятностей и математическая статистика: Учебник Е.С. Кочетков, С.О. Смерчинская, В.В. Соколов; – М. - ФОРУМ, 2008
|
|
|
5. Дискретная математика – учебное пособие. Макоха А.Н., Сахнюк П.А., Червяков Н.И.: учеб. Пособие – М.: ФИЗМАТЛИТ, 2005
6. Высшая математика для экономистов: Практикум для студентов вузов, обучающихся по экономическим специальностям. – Н.Ш. Кремер и др. – М.: ЮНИТИ-ДАНА, 2007
7. Теория вероятностей и математическая статистика. Учебник. Н.И. Сидняев – М.: Издательство Юрайт, 2011
|
|
|
