 |
II. Методические рекомендации по решению
|
|
|
|
ЗАДАЧ И ТЕСТОВ
Тема 1. Спрос, предложение, рыночное равновесие
Задание 1.1.
p; 
p 
1. Вначале построим кривую спроса 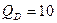при 
, 
, при 
, 
.
Аналогично построим кривую предложения. При , 
; при 
, 
2. В точке равновесия 
, 
. Приравняем два уравнения и определим 
и 
:
; 
.
; 
3. Излишек потребителя 
Излишек производителя 
.
4. Определим 
и 
после введения налога (t) с производителя равного 1 денежной единицы с единицы продукции.
а). Определим вначале уравнение предложения 
после введения налога:
;
.
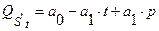б). Определим и после введения налога
5. Определим оптимальную налоговую ставку (t oпт.) и максимальную сумму налога (Т max/).
Вначале необходимо вывести функцию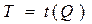 
. (Кривая Лаффера.) Взять от этой функции частную производную, приравнять ее к нулю и определить ставку налога 
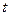, при которой сумма собранного налога 
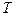будет максимальной.
Предположим, что с каждой единицы продукции произведенной производителем будет взиматься налог t денежных единиц.
а) Определим функцию предложения после введения налога:
или 
;
.
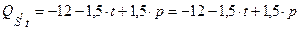б) Выразим равновесие на рынке после введения налога 
:
в) Выразим 
через :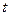
;
.
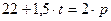г) Представим 
через :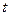
; 
;
.
д) Определим уравнение 
:
е) Определим производную 
ж) Приравняем 
к нулю.
и определим :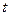 
.
Таким образом при ставке налога 
сумма собранного налога 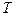будет максимальной.
з) Определим равновесный объем продукции 
после введения налога:
и) Определим максимальную сумму налога при данных кривых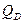 
и 
:
; 
Нанесем новые данные на график.
6. ; 
; .
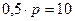7. Определим дефицит при максимальной цене 
; 
; 
.
Определим избыток при минимальной цене 
; 
; 
Избыток QS - QD = 7,5 – 3,5 = 4
8. Определим, как налоговое бремя распределяется между производителем и потребителем при данной ставке налога равной 1 руб. с единицы продукта и при данных уравнении спроса QD = 10 – 0,5р. и уравнении предложения после введения после введения налога QS t = -13.5 + 1.5р.
|
|
|
Если бы производитель всю величину ставки налога включил в цену продажи, то она равнялась бы 12 руб. с единицы продукции. В этом случае он не смог бы реализовать часть продукции как следствие ее перепроизводства при данной цене. Поэтому часть налоговой нагрузки он берет на себя. Это будет зависеть от эластичности спроса и предложения, которые отражаются коэффициентами при независимой переменной этих уравнениях (в и а).
Другая часть налоговой нагрузки переносится на покупателя. Это достижения за счет того, что не вся ставка налога включается в рыночную цену.
Налоговая нагрузка с единицы продукции в нашем примере для покупателя (tпок) будет определятся величиной tпок = Pt* - P* = 11.75 – 11.0 = 0.75 налоговая нагрузка производителя (tпр) выразить величиной tпр = P* - Pr, где Pr – чистая цена, которую получит производитель после уплаты налога
Pr = Pt* - t = 11.75 – 1.0 = 10.75 тогда, сумма налога с единицы продукции, которую заплатит производитель (tпр) будет равна tпр = P* - Pr = 11 – 10,75 = 0,25 руб.
Таким образом, с 1 руб. налога с единицы продукции 0,25 руб. заплатит производитель и 0,75 руб. – потребитель.
Для определения доли ставки налога уплачиваемой производителем (t произ) и потребителем (t пот) можно предложить следующий алгоритм.
Эластичность спроса и предложения по цене, выражаемая с помощью коэффициента эластичности находится во взаимосвязи с коэффициентами уравнения спроса и предложения.
Если взять аппроксимированные уравнения спроса (QD) и предложения (QS) в форме прямых:
– уравнения спроса;
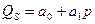– предложения, где р – это цена.
Тогда доля ставки уплачиваемся потребителем (t пот) и производителем (t произ) будет определяться по формулам:
, где t – ставка налога
|
|
|
t = t произ + t пот
Эти величины важные составляющие как с точки зрения распределения налогового бремени, так и для определения уровня рыночной цены после повышения или снижения налоговой ставки.
После повышения налоговой ставки рыночная цена возрастет не на всю величину, а только на ту часть, которую понесет потребитель. В этом случае цена после введения налога (P t) составит:
P t = P * + t пот, где Р * – рыночная цена до введения налога.
Если взять аппроксимированные кривые спроса (QD) и предложения (QS), то на их основе можно определить ставку налога (t) при которой сумма собранного налога (T) будет максимальной применительно к данному товару или услуги.
Изменение ставки налога (t) применяемой к производителю (продавцу) будет оказывать разнонаправленное воздействие на сумму собираемого налога.
С одной стороны рост ставки налога будет оказывать воздействие на снижение объема производства, а соответственно и налогооблагаемой базы.
С другой стороны рост ставки налога будет фактором, который оказывает влияние на увеличение суммы собранного налога.
В условиях разнонаправленного действия двух факторов снижения объема производства и роста ставки налога необходимо определить величины (t), при которой сумма собираемого налога (T) будет максимальной.
Для оптимизации налогообложения при данных уравнениях спроса и предложения выведем уравнение налоговой ставки (t) в общем виде максимизирующей сумму собранного налога (T).
Уравнение спроса 
, уравнение предложения 
.
1. Определим уравнение предложения после введения налога:
.
2. Выразим цену равновесия (pt*) через t.
a0 – a1·t+a1·p=b0 –b1 ·p;
a1·p+ b1 ·p= a1·t- a0+ b0 ;
p(a1+ b1)= a1·t - a0 + b0 ;
p= 
3. Выразим Q через t:
4. Определим уравнение сумму собранного налога:
5. Определим производную T':
6. Приравняем T' к нулю и определим ставку налога t, при которой сумма собранного налога будет максимальной:
Пример. Менеджер фирмы допустил ошибку в прогнозе рыночной конъюнктуры и назначение цену своему товару 12 денежных единиц за 1 шт. товара. По этой цене фирма могла бы реализовать еще 12 шт. продукции. При этом равновесная цена на конкурентном рынке 
составила 
. Функция предложения фирмы имеет вид 
.
|
|
|
Определить уравнение спроса .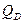
Р е ш е н и е. Определим:
1. Равновесный объем:
; 
.
2. Объем предложения при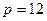 
:
3. Объем продукции, который можно было бы продать при :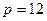
4. Составим уравнение спроса 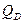по двум точкам:
; 
; 
; 
; 
.
5. Нарисуем график для иллюстрации.
 |
|
|
|
