 |
Статистические величины и их определение
|
|
|
|
Для объективной оценки полученных результатов исследования необходима их математическая обработка.
В технологических исследованиях математическая обработка необходима при изучении показателей состава, свойств и качества сырья и готовой продукции (содержание жира, белка, влаги, консистенции, вязкость, бальная оценка вкуса, запаха и т.д.) в зависимости от технологических параметров производства и условий хранения.
Грамотная обработка экспериментальных данных нередко дает подтвердить реально существующие закономерности, зафиксированные в ходе эксперимента. В НИР обработка экспериментальных данных необходима:
1.Для оценки истинного значения измеряемой величины показателя;
2.Для оценки точности измерения величины показателя;
3.Для оценки сопоставления точности 2 методов анализа, и способов производства
4.Для установления корреляционной и функциональной зависимостей одних свойств объекта с другими
Обработка ЭД проводится с помощью методов математической статистики
Математическая обработка включает расчет, как минимум, следующих статистических величин:
· средняя арифметическая - M;
· среднеквадратичное отклонение единичного результата -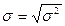 
· стандартное отклонение среднеарифметической или ошибка средней арифметической из всех n повторностей – m ;
· достоверность средней арифметической - t;
· доверительная ошибка оценки измеряемой величины -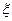 
;
Кроме того, при изучении исследователем влияния каких-либо факторов на параметр технологического процесса необходимо также устанавливать коэффициент корреляции и функциональную зависимость между ними.
Указанные выше статистические величины рассчитываются по формулам:
|
|
|
СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ – М
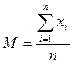; (1)
где xi - значение единичного измерения величины:
n – число повторностей измерений величины.
СРЕДНЕ - КВАДРАТИЧНОЕ ОТКЛОНЕНИЕ - 
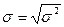; (2)
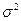- дисперсия, равная 
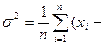M) 2; (3)
следовательно
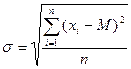; (4)
Величина всегда положительная. Чем больше значение этой величины, следовательно, тем больше изменчивость признака исследуемого объекта. Выражается величина в тех же единицах измерения, что и средняя арифметическая.
Величину определяют с точностью на один десятичный знак больше точности принятой в отношении средней арифметической.
СТАНДАРТНОЕ ОТКЛОНЕНИЕ или ОШИБКА СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ - m
, при n>30 (5)
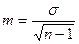, приn<30 (6)
Стандартное отклонение - ошибкасредней арифметическойявляется именованной величиной и выражается так же, как и средняя арифметическая для которой она вычислена. Величину средней и ее ошибку принято записывать так: М + m
Чем меньше величина ошибки средней арифметической, следовательно, тем меньше расхождение между значениями параметра в выборочной и генеральной совокупности.
Ошибку средней арифметической можно выразить в относительных величинах – в процентах (%).. В этом случае её называют показателем точности средней арифметической (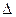
m) и вычисляют по формуле:
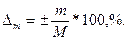(9)
Чем меньше величина 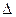m, тем достовернее, надежнее полученная средняя арифметическая измеряемой величины показателя.
АНАЛИЗ ОДНОРОДНОСТИ СРЕДНИХ ЗНАЧЕНИЙ
В научно исследовательской работе часто возникает необходимость сравнения эффективности методов исследования, способов производства или технологических процессов, различающихся либо какими-то условиями (температура, рН, содержание в смеси какого-нибудь компонента, его концентрация и т. д.), либо аппаратурным оформлением процесса.
Для обеспечения возможности такого сравнения по полученным результатам 2 серий опытов измерений для изучаемых методов, способов или аппаратов рассчитывают среднее значение параметра (или выхода) каждой серии М1 и М2 по формуле (1)
|
|
|
Если есть различия в значение параметра, то средние значения будут отличаются друг от друга на величину 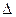М:
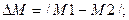(12)
Для достоверной оценки вывода следует для каждого метода или способа рассчитать доверительную ошибку, т.е. (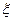
1) и ( 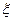2).
Если (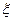 1) будет меньше ( 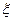2), то можно с заданной вероятностью Р говорить о большей отличительности, существенности значения т.е. эффективности 1 метода исследования, способа, или аппарата.
КОРРЕЛЯЦИОННАЯ ЗАВИСИМОСТЬ
В задачу статистического анализа входят также выявление величины корреляционной связи, и установление типа ее.
Один из основных коэффициентов измеряющих связь между варьирующими признаками X и Y, является коэффициент корреляции R, который находятся в пределах от 0 до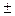 
1. Если R близок к 0, то это указывает на отсутствие связи:
при R = 0,2 – 0,3 – малая связь;
при R = 0,4 - 0,6 – средняя связь;
при R = 0,7- 0,9 связь считается сильной.
Знак минус или плюс у коэффициента корреляции R указывает на направление связи. Знак плюс означает, что связь между признаками X и Y прямая (положительная), знак минус - связь обратная (отрицательная).
Коэффициент корреляции выявляет величину и направление связи лишь тогда, когда связь между признаками близка к прямолинейной. Поэтому прежде чем вычислить коэффициент корреляции, необходимо установить, какой тип связи может быть между X и Y: близкий к прямолинейной или сильно выраженный криволинейный. Это достигается путем анализа литературных данных или нанесения опытных данных на рисунок в координатах по X и Y.
Рассчитывают коэффициент корреляции по формуле 13
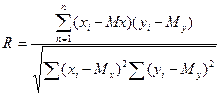, (13)
где xi и Mx – значение единичного результата и средняя арифметическая одного признака;
yi и My - значение единичного результата и средняя арифметическая другого зависимого признака.
ОПРЕДЕЛЕНИЕ УРАВНЕНИЯ РЕГРЕССИИ
Влияние какого-либо фактора –X на выход процесса –Y в общем виде выражается уравнением регрессии Y= f(x)/
Наиболее часто встречающиеся в технологических исследованиях виды зависимостей линии регрессии показаны графически на рис.1.
Этапы обработки полученных результатов исследования для определения искомого уравнения регрессии.
|
|
|
1. Определение среднего значения результата (X; Y) у средней оценки дисперсии единичного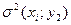 
и среднего 
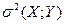результатов
2. Построение графической зависимости Y= f(x) и установление того или иного вида искомого уравнения (линейное, квадратичное, степенное, и т д., рис 1.)
3. Определение коэффициентов искомого уравнения Проверка адекватности (соответствия) полученного уравнения экспериментальным данным и оценка точности аппроксимации. Если уравнение недостаточно точно описывает экспериментальные данные, то следует выбрать другой вид уравнения, перейти к полиному, более высокой степени.
ОЦЕНКА ТОЧНСТИ АПРОКСИМАЦИИ
Точность аппроксимации оценивается при уравнении регрессии любого вида коэффициентом аппроксимации Ё (в процентах), который вычисляется по формуле
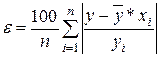(14)
Точность аппроксимации считается удовлетворительной, если e<=10%
|
|
|
