Влияние атмосферы на распространение лазерного и оптического излучения

Высокие потенциальные возможности лазерных локационных систем в ряде случаев ограничиваются из-за искажений сигналов при их распространении в атмосфере. Влияние атмосферы проявляется в виде поглощения и рассеяния волн молекулами и аэрозолями атмосферы и флуктуаций показателя преломления. Поглощение и рассеяние являются причиной ослабления лазерного и оптического излучения и учитываются обычно введением соответствующих коэффициентов пропускания 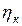. В то же время случайные изменения показателя преломления, обусловленные атмосферной турбулентностью, приводят к амплитудно – фазовым искажениям волнового фронта излучения, что в результате приводит к уширению и блужданию лазерного пучка, к искажениям изображений и т.д. В конечном счёте, все это снижает потенциал лазерных систем и не позволяет эффективно решать задачи формирования изображений.

Основной причиной флуктуаций показателя преломления в воздухе является турбулентное (вихревое) перемешивание слоев атмосферы, имеющих разную температуру. Диэлектрическую проницаемость атмосферного воздуха принято описывать случайной функцией координат и времени , где  - пространственно частотный радиус – вектор, t – время. Обычно считают, что среднее значение этого случайного поля 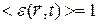  и вводят величину , описывающую флуктуации диэлектрической проницаемости

                                     .                                               (П2.1)   

Величина пульсаций  в атмосфере имеет порядок  ~ 10^-6 – 10^-5 (безразмерная величина). С учетом того, что для атмосферы уровень флуктуаций магнитной проницаемости , можно считать и показатель преломления , где c – скорость света в вакууме, а v – скорость света в среде, имеющей диэлектрическую проницаемость , равен (поскольку, согласно Максвеллу, ). Поэтому для флуктуаций показателя преломления имеем

       .            (П2.2) 

Основные результаты для турбулентного движения получены в рамках т.н. модели Колмогорова – Обухова. Согласно этой модели турбулентные флуктуации диэлектрической проницаемости являются многомасштабными, т.е. возникают вихри разных размеров (масштабов). Верхняя граница пространственного масштаба флуктуаций ограничена размером рассматриваемого слоя воздуха и называется внешним масштабом турбулентности   L ₀. При изучении флуктуаций параметров волн, распространяющихся через всю толщу атмосферы, величина L ₀ имеет порядок толщины атмосферного слоя (10 ÷ 30 км). Если трасса распространения волны приземная, то L ₀ по порядку величины совпадает с высотой трассы z. При этом, хотя в потоке могут присутствовать и более крупные вихри, однако при наблюдении их на высоте z они воспринимаются не как отдельные вихри, а как изменение потока в целом. Вихри более мелких масштабов образуются путем деления крупномасштабных вихрей с передачей им их энергии. Такое деление происходит до тех пор, пока не начнут сказываться силы вязкости воздуха. Нижний характерный масштаб вихрей l ₀, присутствующий в турбулентной среде, при котором уже не наблюдается деления и передачи энергии, называется внутренним масштабом турбулентности. Величина l ₀ в реальной атмосфере в зависимости от погодных условий может принимать значения от 1 мм до десятков сантиметров.

Случайные изменения показателя преломления турбулентной атмосферы первоначально приводят к искажению только фазы волнового фронта. Однако по мере дальнейшего распространения оптического излучения случайная интерференция вторичных волн, рассеянных неоднородностями показателя преломления, вызывает флуктуации и его амплитуды. Таким образом, в общем случае функцию атмосферного изменения принимаемого поля на апертуре можно представить в виде

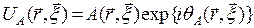    ,                            (П2.3)

где  и  - действительные функции, соответствующие амплитудным и фазовым флуктуациям оптического сигнала в турбулентной атмосфере;  и 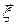 - двумерные векторы в плоскости объекта и апертуры, соответственно.          

Для дальнейшего рассмотрения введем понятие угла изопланатизма. Это телесный угол , в котором наблюдается объект и который характеризуется тем, что атмосферные искажения, вносимые в поле точечного источника, излучающего из точки , расположенной в этом угле в плоскости объекта, к точке 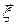 апертурной плоскости, являются одними и теми же для всех других точек, лежащих внутри этого угла. При наблюдении объектов, угловые размеры которых , функцию (П2.3) можно представить в виде

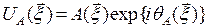       .                                          (П2.4)

В этом случае справедливо т.н. приближение «амплитудно-фазового экрана». Величина угла изопланатизма зависит от силы турбулентности (значения структурной постоянной ) и изменяется в пределах от единиц до десятков угловых секунд, а в некоторых случаях и до единиц градусов.                               

Влияние амплитудных и фазовых флуктуаций по-разному сказывается на информационной структуре оптического сигнала. На рис.П2.1 показаны смоделированные для полоскового телескопа изображения точечного объекта при отсутствии атмосферных искажений (а), наличии случайных амплитудных флуктуаций в приходящем волновом фронте (б) и наличии случайных фазовых флуктуаций (в). Из рисунка видно, что амплитудные флуктуации просто уменьшают высоту центрального максимума, тогда как фазовые флуктуации полностью разваливают его, давая «пятенную» картину. Таким образом, основное влияние на оптический сигнал оказывают именно фазовые искажения в турбулентной атмосфере.

 

	Рис.П2.1 Изображения точечного источника.

 

 

С учетом сказанного, функцию атмосферного изменения поля (П2.4) можно переписать в виде

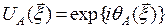                                     (П2.5) 

Модель турбулентных искажений оптического поля (П2.5) в литературе получила название «фазового экрана». В дальнейшем мы будем пользоваться, в основном, этой моделью.

Если протяженность турбулентной трассы L много больше размеров отдельных неоднородностей показателя преломления, то на основании центральной предельной теоремы можно показать, что случайная функция  распределена по нормальному закону с нулевым средним 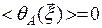 и среднеквадратичным отклонением 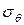. При 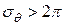  можно считать, что фазовые флуктуации  равномерно распределены в интервале . Среднее поле   с учетом известной формулы

,

которая справедлива для любой нормальной величины x с < x >=0, можно представить в виде

                                            .                                             (П2.6) 

Нетрудно видеть, что при 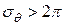. Для корреляционной функции поля   выражение

                .                           (П2.7)

Здесь 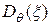 - поперечная (в плоскости, перпендикулярной линии распространения) структурная функция фазовых флуктуаций на апертуре

.

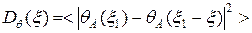Для сферической волны, прошедшей путь L в турбулентной среде, 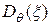 равна

                 ,                           (П2.8)

где  - волновое число; - зенитный угол;  - высотный профиль структурного параметра показателя преломления вдоль трассы распространения            ().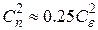 

Для дальнейшего рассмотрения введем пространственный параметр , определяемый как

             .                         (П2.9) 

Эта величина называется параметром Фрида и имеет смысл пространственного радиуса корреляции атмосферных искажения поля оптического излучения (П2.5). Типичное значение  для средней атмосферы составляет, примерно, 10 см.

С учетом (П2.9) выражения для структурной и корреляционной функций приобретают простой вид

                      ,                                             (П2.10)

                          .                                          (П2.11)

Для дисперсии фазовых флуктуаций справедливо выражение

                    .                                               (П2.12)

Таким образом, уровень фазовых флуктуаций определяется отношением диаметра апертуры к пространственному радиусу корреляции поля атмосферных искажений или, другими словами, числом корреляционных ячеек случайного поля , укладывающихся на апертуре, т.е. величиной (D / r ₀)².  

Модель турбулентных искажений «фазовый экран», предполагающая наличие множества (при больших значениях D / r ₀) корреляционных ячеек на апертуре телескопа, приводит к достаточно простому физическому объяснению процесса формирования картины поля при распространении лазерного излучения, например, в фокальной плоскости линзы при формировании изображения или в зоне Фраунгофера при локации удаленного объекта. Интерференция случайных полей приводит к уширению лазерного пучка, а при сильных искажениях (D / r ₀>>1) и к появлению отдельных «пятен», как это видно из рис.П2.1в. В результате такого случайного (некогерентного) сложения пучков реальная разрешающая способность или расходимость δ оптической системы определяется уже не размерами ее апертуры D, а величиной r ₀, т.е. по Рэлею

.

Размер «размазанного» вследствие атмосферных искажений изображения точечного источника будем называть пятном атмосферного видения. Его линейный размер (диаметр) равен 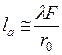, где F – фокусное расстояние приемной оптической системы. (В отличие от размера пятна от точечного источника в свободном пространстве, которое определяется дифракцией света на апертуре диаметра D и равно ). Из рис. П2.1а видно, что  в относительных единицах равно 0.2, тогда как , как следует из рис.П2.1в, равно 0.8, т.е. включает в себя всю пятенную картину.  

Еще одним существенным негативным влиянием, к которому приводят фазовые искажения в турбулентной атмосфере, являются флуктуации угла прихода пучка или наклона волнового фронта . Они связаны с флуктуациями разности фаз в поперечной плоскости пучка между точками, находящимися на расстоянии . Из выражения для структурной функции (П2.8) непосредственно следует, что дисперсия угла наклона волнового фронта на апертуре диаметра D равна

.

Рассмотрим теперь временные характеристики атмосферных флуктуаций. Они могут быть получены в рамках гипотезы «замороженной атмосферы», которая формулируется математически следующим образом

                                ,                                               (П2.13)     

где  - вектор поперечной скорости ветра в плоскости апертуры. Физический смысл этой формулы заключается в том, что турбулентность как бы «плывет» вдоль апертуры в направлении заданной скорости ветра. Время, в течение которого она проходит расстояние r ₀, т.е. расстояние, равное пространственному интервалу корреляции, называется временем «замороженности» атмосферы  и имеет смысл временного интервала корреляции атмосферных искажений

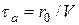                                    ,                                                            (П2.14)

где . Подставляя (П2.9) в (П2.14) получаем окончательное выражение для  

                 ,               (П2.15)  

где V (h) – высотный профиль скорости ветра вдоль трассы распространения излучения. По порядку величины  изменяется от единиц до десятков мс. Например, для       r ₀=10 см и средней скорости ветра V =10 м/с время замороженности равно 10 мс. Это означает, что полоса частот атмосферных флуктуаций для средней турбулентности составляет 100 Гц.

 

 

Литература

 

1. Гальярди Р.М., Карп Ш. Оптическая связь. Пер. с англ. под ред. А.Г.Шереметьева. М.:

Связь, 1978.

2. Пратт В.К. Лазерные системы связи. Пер. с англ. под ред. А.Г.Шереметьева. М.: Связь,

1972.

3. Малашин М.С., Каминский Р.П., Борисов Ю.Б. Основы проектирования лазерных

локационных систем. М: Высшая школа, 1983.

                                                                           

 

                                      

                                                                                                                                                                                                                                                                                                                                                                   

                                                                               

                                                                                       

 

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: