Главная | Обратная связь | Поможем написать вашу работу!

Уравнения и неравенства с одной переменной, их решение.

Тема 2_0 Числовые системы

Введение. Развитие понятия числа

Числа 1, 2, 3, 4, …… - множество натуральных чисел (N)

Числа , ……. - множество целых чисел (Z)

Числа - множество рациональных чисел (Q)

Любое рациональное число можно записать в виде дроби , где m Z, n N

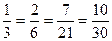
и т.д.

Разделив "m" на "n" получаем конечную или бесконечную десятичную дробь

Как видим, у некоторых дробей десятичные знаки повторяются

0,5555 ……; 0,3333 ……; 4,5222 …….;

Такие числа называются периодическими десятичными дробями и записываются:

4,959595 … = 4, (95) 2,125125125 … = 2, (125)

0,5121212 … = 0,5 (12) 2,13444 … = 2,13 (4)

Каждая бесконечная периодическая дробь представляет собой рациональное число (докажем несколько позже), а пока будем использовать правило записи в виде обыкновенной дроби:

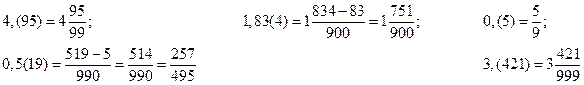
для чисто периодической дроби: в числителе пишется число, стоящее в периоде, а в знаменателе столько "9", сколько цифр в периоде, целая часть остается без изменения.

для смешанной периодической дроби: в числителе разность между числом, стоящим после запятой, и числом, стоящим после запятой до периода, а в знаменателе столько "9", сколько цифр в периоде, со столькими "0", сколько цифр после запятой до периода

Запишите в виде обыкновенной дроби:

5,21 (3) 13, (71) 14,72 (24) 0, (4)

0,7 (125) 10, (125)

Числа, представляющие собой бесконечные непериодические десятичные дроби, называются иррациональными:

4,1728 …. 0,1078612 … 13,200941 …

Вы уже знакомы с числовыми множествами, называемыми промежутками. Перечислим их.

Отрезок с концами а и b:

[a;b] =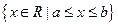

Интервал с концами a и b

(a,b) =

Полуоткрытые промежутки:

(a,b] = ; [a,b) =

Число b - а называется длиной промежутка

Бесконечные промежутки(лучи, полупрямые):

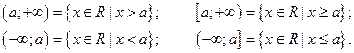
Числовая прямая: 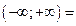R

Интервал вида называют также - окрестностью точки а

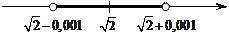Можно сказать, например, что все десятичные приближения по недостатку и по избытку к числу , начиная с третьего (т.е. приближения с точностью до 10^{- n}при n 3), попадают в - окрестность точки при = 0,001.

При выполнении действий над действительными числами используют правила округления числа

4,762 4,76 (с точностью до 0,01)

4,762 4,8 (с точностью до 0,1)

4,762 5 (с точностью до целых чисел)

Формулы сокращенного умножения

Выполнить действия (самостоятельно)

1. (4а + 3с)²2. (х³- 2у + 3ху)² 3. (2х - 3у²- х³у)²

4. (х²- 3у) (х²+ 3у) 5. (х + 2у) (х² - 2ху + 4у²)

Мнимая единица. Комплексные числа. Действия над комплексными числами.

х² + 4 = 0 х² = - 4 во множестве R решений нет

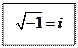Обозначим:

Множество действительных чисел и мнимая единица составляют множество комплексных чисел, тогда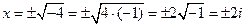

i ²³ = i ³ = - i (23: 4 = 4 5 + 3)

i ²³ = i ²⁰ i ³ = 1 (-i) = - i

i ⁴⁸ = i⁰ = 1 i ¹⁰ i ⁸ i ² = 1 (-1) = -1 i ¹⁴ = i ² = - 1 i ²⁵ = i ¹ = i

i ¹⁰³ = i³ = - i 2 i³ - 7 i ⁸ + 5 i ⁹ + 4 i¹⁰ = - 2 i - 7 + 5 i - 4 = - 11 + 3 i

Число Z = a + b i - комплексное число (алгебраическая форма записи)

а - действительная часть числа

b i - мнимая часть числа

a + b i = a₁ + b₁ i если а = а₁ b = b₁

a + b i и a - b i называются сопряженными

Например

2 - 3 i и 2 + 3 i

- 4 - i и - 4 + i, т. е. отличаются знаком перед мнимой частью

Числа a + b i и - a - b i называются противоположными

Например

- 3 - 4 i и 3 + 4 i

- 5 + 2 i и 5 - 2 i, т.е. отличаются знаками и перед мнимой и перед действительной частями

Комплексные числа изображаются геометрически точкой (a; b) или радиусом - вектором, проведенным к этой точке из начала координат

Z ₁ = 5i Z ₂ = 2 Z ₃ = - 3i Z ₄ = - 4i

Z = 3 - 4 i Z = - 2 + 3 i

Изобразите числа:

Z = - 7 + 2 i Z = - 9 - i

Z = - 1 - 4 i Z = 12

Z = - 5 i Z = 6 i

Z = - 4 Z = - 3 - 2 i

Итак: a + bi

a OX I ч j > 0 острый

b OY II ч j > 0 тупой j = 180 ⁰ - j₁

III ч j < 0; тупой j = - (180 ⁰ - j₁)

IV ч j < 0; острый

– модуль комплексного числа

аргумент комплексного числа

Найти модуль и аргумент комплексного числа:

а) Z = 5 + 2 i

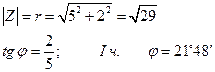
б) Z = - 3 + 7 i

в) Z = - 5 - i

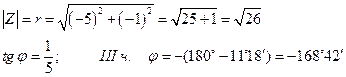
г) Z = 3 - 5 i

Для чисел, состоящих только из мнимой или только действительной частей нахождение и упрощается:

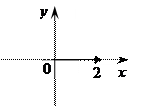1) Z = 2

2 = 2 + 0i Число находится на "ОХ"

2) Z = 3i

3i = 0 + 3i Число находится на "ОУ"

3) Z = - 4

Число находится на "ОХ" (влево)

4) Z = - 7 i

Число находится на "ОУ" (вниз)

Самостоятельно

Найти модуль и аргумент комплексного числа

1. Z = - 4 + 3 I 3. Z = - 3 - 7 I 5. Z = - 7 I 7. Z = 3 i

2. Z = - 2 - 5 I 4. Z = 5 + I 6. Z = 2 8. Z = - 4

Z₁ = a ₁ + b ₁ i

Пусть даны числа: Z₂ = a ₂ + b ₂ i

Рассмотрим действия над числами

Сложение

Z₁+ Z₂ = (a ₁ + b ₁ i) + (a ₂ + b ₂ i) = a ₁ + b ₁ i + a ₂ + b ₂ i = (a ₁ + a ₂) + (b ₁ + b ₂) i

Вычитание

Z₁- Z₂ = (a ₁ + b ₁ i) - (a ₂ + b ₂ i) = a ₁ + b ₁ i - a ₂ - b ₂ i = (a ₁ - a ₂) + (b ₁ - b ₂) i

Умножение

Z₁ Z₂ = (a ₁ + b ₁ i) (a ₂ + b ₂ i) = a ₁ a ₂ + b ₁ а ₂i + a ₁ b ₂ i + b₁ b ₂i ² =

= a ₁ a ₂ + i (b ₁ а ₂ + a ₁ b ₂) - b ₁ b ₂ = (a ₁ a ₂ - b₁ b ₂) + (b ₁ а ₂ + a ₁ b ₂) i

Например

1) (3 - 5 i) (- 3 + i) = - 9 + 15 i + 3 i - 5 i ² = - 9 +18 i + 5 = - 4 + 18i;

т.к. i ² = - 1, то -5 (-1) = 5

2) (2 - 3 i) (2 + 3 i) = 4 - 9 i ² = 4 + 9 = 13

(a + b i) (a - b i) = a ²- b ² i ² = a ² + b²

Сумма квадратов

Сумма квадратов разлагается на множители только во множестве комплексных чисел

Деление

конкретно на примере:

Возведение в квадрат, куб (используем формулы сокращенного умножения)

Z = (a + b i) ²= a ² + 2 a b i + b ² i ² = a ²+ 2 a b i - b ²;

например:

1) (- 4 + i) ² = 16 - 8 i + i² = 16 - 8 i - 1 = 15 - 8 i

2) (2 - 3 i) ³ = 8 - 3 2² 3 i + 3 2 (- 3 i) ² - 27 i ³ = 8 - 36 i + 54 i ² - 27 i ³ =

= 8 - 36 i - 54 + 27 i = - 46 - 9 i

Выполнить действия

при этих действиях использованы правила: i ³ = - i; i ² = - 1; (a - b) ² = a ² - 2 a b + b ², а теперь разделим, для этого умножим знаменатель на сопряженное ему число (- 5 + 12 i), а чтобы дробь не изменилась умножаем и числитель на это число, т.е.

Самостоятельно

Выполнить действия

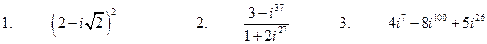
Контрольные вопросы

1. Что принято за мнимую единицу?

2. Чему равно

3. Какое число называется комплексным числом?

4. Какие комплексные числа называются сопряженными, противоположными?

5. Как найти i в любой степени?

6. Как изображается геометрически комплексное число?

7. Чему равен модуль комплексного числа?

8. Как находится аргумент комплексного числа?

9. Как выполняются действия сложение и вычитание комплексных чисел?

10. Как выполняется умножение комплексных чисел?

11. Чему равно произведение двух сопряженных комплексных чисел?

12. Как выполняется деление комплексных чисел?

Уравнения и неравенства с одной переменной, их решение.

– линейное уравнение I степени с одной переменной

– уравнение II степени с одной переменной

Решить уравнение – значит найти множество его корней или доказать, что их нет. это множество называют решением уравнения.

Два уравнения называются равносильными если решение (корень) одного уравнения является решением (корнем) другого уравнения и наоборот.

Уравнения 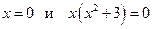равносильны, так как оба имеют единственный корень .

Уравнения и – неравносильны, так как является корнем первого уравнения, но не удовлетворяет второму уравнению.

Уравнения 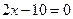и неравносильны, так как корень первого уравнения , а второе уравнение кроме этого корня имеет еще корень , который не является корнем первого уравнения.

Решим уравнения:

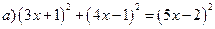
раскроем скобки, применяя формулы сокращенного умножения 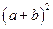и

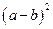
приведем подобные члены, получим

Ответ: – корень уравнения.

разложим на множители

перенесем все члены уравнения в левую часть и приведем дроби к общему знаменателю

дробь равна нулю, когда её числитель равен нулю, а знаменатель не равен нулю, т. е.

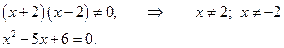
Решаем уравнение

Так как – посторонний корень и решением уравнения будет . Ответ: .

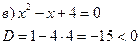
уравнение не имеет действительных корней. Найдем мнимые корни.

(мы знаем, что – мнимая единица)

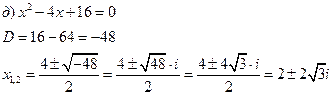
Самостоятельно

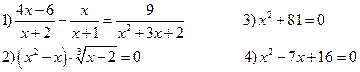
– неравенства I степени с одной переменной

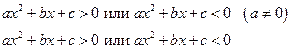– неравенства II степени с одной переменной

Решить неравенство – значит найти множество значений переменной, при которых это неравенство является верным.

Два неравенства называются равносильными, если множество решений этих неравенств совпадают.

Решим неравенства

а)

Перенесем все члены в левую часть и приведем к общему знаменателю. общий знаменатель 10; так как знаменатель не содержит переменной, то есть сразу видно чт часть и приведем к общему знаменателю. общий знаменатель 10; так как знаменатель не содержит перемено он не равен нулю, то в дальнейшем его можно не писать (опустить).

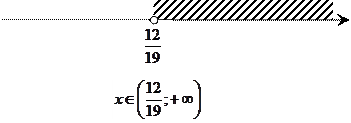
б)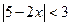

, то есть

Используя свойства числовых неравенств, имеем

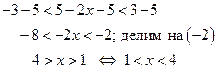, знак неравенства меняется на противоположный

Или можно записать в виде системы неравенств

в)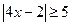

Решаем две системы

Ответ: .

г)

умножим на (–1)

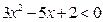
квадратное неравенство

Найдем корни уравнения

Графиком функции является парабола, ветви которой направлены вверх, а точки пересечения параболы и оси OX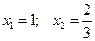

Изобразим геометрически:

или

получаем три интервала, в которых определяем знак трехчлена. Так как мы решаем неравенство , то решением неравенства будет промежуток (интервал)

действительных корней нет, так как ветви параболы направлены вверх, то парабола не пересекает ось и расположена выше её, где всегда > 0,

а мы решаем неравенство , значит данное неравенство не имеет решения.

уравнение не имеет действительных корней, т.е. парабола не пересекает ось, ветви параболы направлены вверх,

а так как мы решаем неравенство 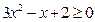, то оно имеет множество решений, т.е. .

то оно имеет множество решений, т.е. е пересекает ось, ветви параболы направлены вверх, т.е. даж) 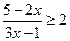– дробно–рациональное неравенство, которое может быть решено или через системы неравенств или методом интервалов. Перенесем правую часть в левую, приведем подобные члены

Решим через системы неравенств. Дробь < 0, если числитель и знаменатель имеют разные знаки, т.е.

(Дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю).

При решении системы неравенств надо решить каждое неравенство и выбрать общие промежутки.

Решаем

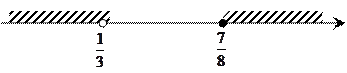
система не имеет решения. Следовательно решением данного неравенства является .

Метод интервалов позволяет ускорить процесс решения неравенства корни и .

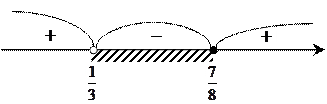
Метод интервалов позволяет решать не только неравенства II степени, дробно–рациональные но и более высоких степеней.

находим корни многочлена

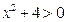всегда, т.е. действительных корней нет.

Отметим корни на числовой прямой, учитываем, что числитель может быть равен нулю.

только определяем знак выражения в каждом промежутке

и тогда решением неравенства является .

Можно несколько ускорить процесс определения знака в промежутках.

В промежутке больше большего корня всегда выражение больше нуля, а затем, если корень повторяется нечетное число раз (кратность его нечетная), то знаки в промежутках справа и слева от корня изменяются, а если кратность корня четная, то знак справа и слева от корня не изменяется.

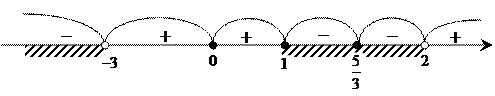
, так как , то 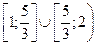можно записать

и тогда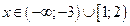

Самостоятельно:

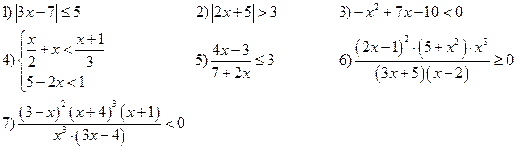
12 3	Поделиться:

Воспользуйтесь поиском по сайту: