 |
Занятие 1.7 Системы нелинейных уравнений
|
|
|
|
- Понятие системы нелинейных уравнений.
- Решение систем нелинейных уравнений.
- Вычисления при помощи МК.
Система уравнений, в которой хотя бы одно из уравнений содержит переменную во второй или выше степени называется нелинейной системой уравнений. Решить систему – значит найти все ее решения. Решением системы называется пара чисел, удовлетворяющая каждому из уравнений системы. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Система называется определенной, если она имеет конечное число решений, и неопределенной, если она имеет бесконечное множество решений.
Две системы называются равносильными, если они имеют одно и то же множество решений.
При решении систем нелинейных уравнений наиболее широко используются методы: 1. подстановки; 2. алгебраического сложения; 3. графический; 4. искусственные приемы (применение формул сокращенного умножения, введения новой переменной, использование теоремы Виета и т.д.).
Рассмотрим примеры решения систем уравнений.
1. Решить способом подстановки.

первое уравнение содержит одну переменную, можно выписать это уравнение и решить его.
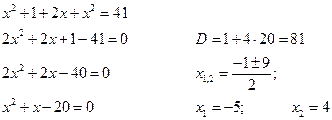
и тогда, подставив полученные значения  и
и  во второе уравнение, получаем
во второе уравнение, получаем

Получаем две пары чисел  , которые являются решением данной системы уравнений. Ответ: (5; –4); (4; 5).
, которые являются решением данной системы уравнений. Ответ: (5; –4); (4; 5).
2. Решить способом алгебраического сложения
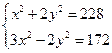
Видим, что каждое из уравнений содержит  , сложим почленно и получаем уравнение относительно одной переменной.
, сложим почленно и получаем уравнение относительно одной переменной.

И тогда имеем  и
и  , т.к. системы содержат только
, т.к. системы содержат только  , а
, а 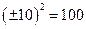 , то можно решить только одну из систем и получить значения y
, то можно решить только одну из систем и получить значения y
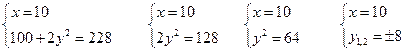
 И тогда решением системы будут
И тогда решением системы будут  и
и  .
.
|
|
|
3. Решить графически

Графическое решение системы уравнений с двумя переменными сводится к отысканию координат общих точек графиков уравнений:
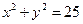 – окружность с центром (0; 0) и R = 5
– окружность с центром (0; 0) и R = 5
 – гипербола
– гипербола
| x | 2 | 3 | 4 | 6 | –1 | –2 | –3 | –4 | –6 |
| y | 6 | 4 | 3 | 2 | –12 | –6 | –4 | –3 | –2 |
Имеем пары чисел (3; 4); (4; 3); (–3; –4); (–4; –3) которые определяют координаты четырех точек.
4. Решить систему уравнений введением новой переменной.
 левая часть каждого из уравнений системы есть однородный (одинаковой степени) многочлен относительно переменных x и y.
левая часть каждого из уравнений системы есть однородный (одинаковой степени) многочлен относительно переменных x и y.
Пусть y = xt

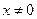 , т.к. тогда и
, т.к. тогда и 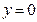 , что невозможно.
, что невозможно.
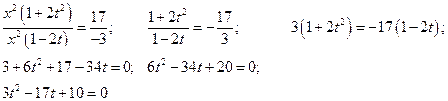
Решаем уравнение относительно t

Теперь можно записать системы уравнений
 и
и 
Решаем способом подстановки первую систему:

Аналогично решение второй системы:

Таким образом получаем пары чисел: 
4. 
Пусть  и
и  , тогда имеем систему уравнений
, тогда имеем систему уравнений

Применим способ алгебраического сложения
 , тогда
, тогда 
Следовательно имеем систему уравнений

 подставив значение
подставив значение  в любое из уравнений системы
в любое из уравнений системы
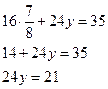
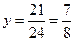 т.е. решением системы является пара чисел
т.е. решением системы является пара чисел 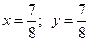


Решаем второе уравнение относительно y;
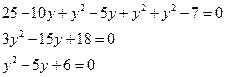 по теореме Виета имеем
по теореме Виета имеем  ,
,
тогда  , т.е. решением системы будут пары чисел
, т.е. решением системы будут пары чисел  и
и 


 упростим первое уравнение системы с помощью введения новой переменной
упростим первое уравнение системы с помощью введения новой переменной
Пусть  , тогда
, тогда  и уравнение имеет вид
и уравнение имеет вид  т.к.
т.к. 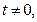 то
то

и тогда имеем системы
 и
и 
Решаем эти системы относительно x и y
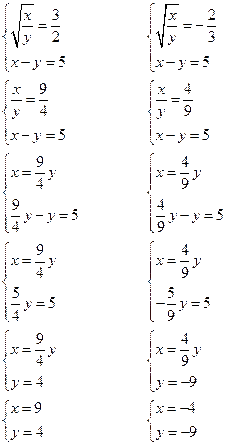
Ответ: (9; 4); (–4; –9).
Замечание. При решении систем нелинейных уравнений предварительно надо решить, каким методом может быть решена система, какие надо выполнить преобразования, какие операции приводят к упрощению систем.
Самостоятельно:
1)  3)
3) 
2)  4)
4) 
Вычислить при помощи МК.
Занятие 1.8 Зачет по теме. Практическая работа
(решение примеров)
1. Собеседование по теоретическим вопросам темы (модуля) (приложение 3).
|
|
|
2. Письменная работа (приложение 4).
3. Выполнение практической работы (практическая работа № 1).
Приложение 1
Домашнее задание № 1
Вариант I
Решить уравнения: Решить неравенства:


Вариант II
Решить уравнения: Решить неравенства:
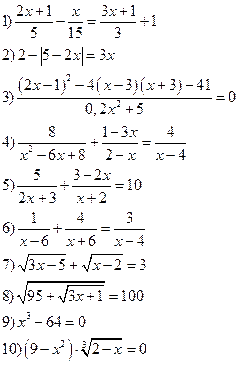

Вариант III
Решить уравнения: Решить неравенства:


Вариант IV
Решить уравнения: Решить неравенства:
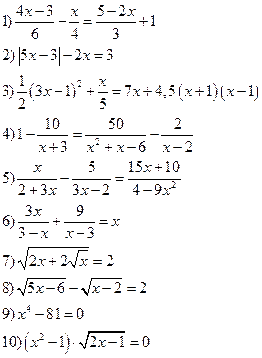

Вариант V
Решить уравнения: Решить неравенства:
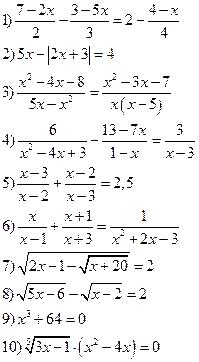
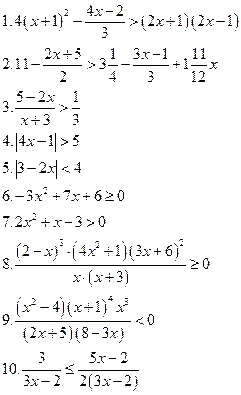
Вариант VI
Решить уравнения: Решить неравенства:
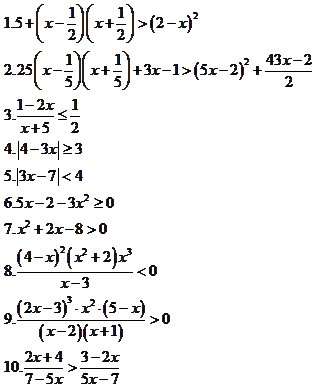

Вариант VII
Решить уравнения: Решить неравенства:


Вариант VIII
Решить уравнения: Решить неравенства:


Вариант IX
Решить уравнения: Решить неравенства:


Вариант X
Решить уравнения: Решить неравенства:


Приложение 2
Домашнее задание № 2
Вариант I
Решить системы уравнений:

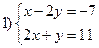

Вариант II
Решить системы уравнений:


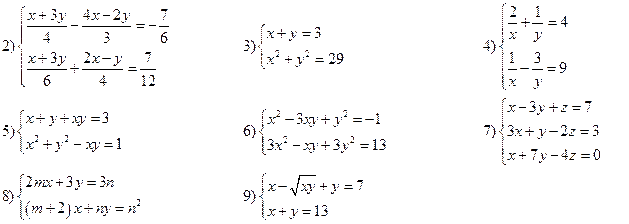
Вариант III
Решить системы уравнений:



Вариант IV
Решить системы уравнений:



Вариант V
Решить системы уравнений:



Вариант VI
Решить системы уравнений:



Вариант VII
Решить системы уравнений:

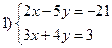
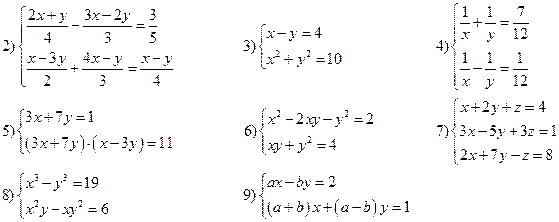
Вариант VIII
Решить системы уравнений:

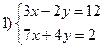

Вариант IX
Решить системы уравнений:

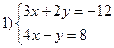

Вариант X
Решить системы уравнений:


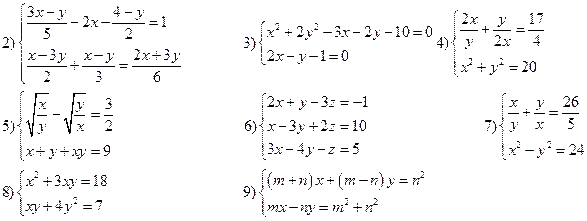
Приложение 3
Контрольные зачетные вопросы по теме
1) Какие числа называются рациональными?
2) Какие числа называются иррациональными?
3) Какие числа называются действительными?
4) Геометрическое изображение действительных чисел.
5) Правила записи десятичной периодической дроби в виде обыкновенной.
6) Формулы сокращенного умножения.
7) Формула решения квадратного уравнения (дискриминант, нахождение корней уравнения).
8) Формула разложения квадратного трехчлена на множители.
9) Решение биквадратных уравнений.
10) Решение иррациональных уравнений.
11) Решение неравенств с одной переменной. Метод интервалов. (его сущность)
12) Мнимая единица, степень мнимой единицы.
|
|
|
13) Что называется комплексным числом?
14) Какие комплексные числа называются противоположными? сопряженными?
15) Геометрическое изображение комплексных чисел.
16) Модуль комплексного числа, его вычисление.
17) Аргумент комплексного числа, его нахождение.
18) Сложение и вычитание комплексных чисел.
19) Умножение комплексных чисел в алгебраической форме. Разложение  на множители.
на множители.
20) Деление комплексных чисел в алгебраической форме.
21) Определитель II порядка, его вычисление, свойства.
22) Определитель III порядка, его вычисление, свойства.
23) Правила нахождения определителей  .
.
24) Правило Крамера при решении систем линейных уравнений.
Приложение 4
|
|
|


