 |
Пример текста программы для М-файла
|
|
|
|
| A=[1 2 3;1 2 1;3 2 0] disp('At-транспонирование A:'),At=A' B=[4 1 2; 0 4 3;1 1 1] disp('Bt-транспонирование B:'),Bt=B' disp('p,q,r-столбцы:') p=[.1;1.7;-1.5] q=[-1.6;0.8;1.1] r=[-0.7;1.3;0.2] disp('матрица PQR=[p q r]:'),PQR=[p q r] disp('p,q,r-строки:') p=[.1 1.7 -1.5] q=[-1.6 0.8 1.1] r=[-0.7 1.3 0.2] |
Результаты счета в командном окне
A =
1 2 3
1 2 1
3 2 0
At-транспонирование A:
At =
1 1 3
2 2 2
3 1 0
B =
4 1 2
0 4 3
1 1 1
Bt-транспонирование B:
Bt =
4 0 1
1 4 1
2 3 1
p,q,r-столбцы:
p =
0.1000
1.7000
-1.5000
q =
-1.6000
0.8000
1.1000
r =
-0.7000
1.3000
0.2000
матрица PQR=[p q r]:
PQR =
0.1000 -1.6000 -0.7000
1.7000 0.8000 1.3000
-1.5000 1.1000 0.2000
p,q,r-строки:
p =
0.1000 1.7000 -1.5000
q =
-1.6000 0.8000 1.1000
r =
-0.7000 1.3000 0.2000
>>
Пример 2. Вычислить для матриц А и В:
– определение обратных матриц,
– матричное и поэлементное произведение,
– матричное и поэлементное возведение в степень 4,
– матричное и поэлементное деление,
– сложение матрицы с числом,
- умножение матрицы на число,
где
; 
;
Пример текста программы для М-файла
A=[1 2 3;1 2 1;3 2 3]
B=[4 1 2; 3 4 3;1 1 1]
A1=inv(A);disp('обратная матрица к матрице А: A1='),disp(A1)
B1=inv(B);disp('обратная матрица к матрице B: B1='),disp(B1)
disp('матричное произведение А*B='),disp(A*B)
disp('поэлементное произведение А.*B='),disp(A.*B)
disp('матричное возведение в степень А^4='),disp(A^4)
disp('поэлементное возведение в степень А.^4='),disp(A.^4)
disp('операция умножения обратной матрицы А на матрицу B: A\B='),disp(A\B)
disp('операция умножения А на обратную матрицу B: A/B='),disp(A/B)
disp('поэлементное деление А./B='),disp(A./B)
disp('поэлементное деление А.\B='),disp(A.\B)
disp('операция умножения А на число 2: 2*A='),disp(2*A)
disp('операция сложения матрицы А с числом 2: 2+A='),disp(2+A)
Результаты счета в командном окне
A =
1 2 3
1 2 1
3 2 3
B =
4 1 2
3 4 3
1 1 1
обратная матрица к матрице А: A1=
-0.5000 0.0000 0.5000
0 0.7500 -0.2500
0.5000 -0.5000 0
обратная матрица к матрице B: B1=
|
|
|
0.5000 0.5000 -2.5000
0 1.0000 -3.0000
-0.5000 -1.5000 6.5000
матричное произведение А*B=
13 12 11
11 10 9
21 14 15
поэлементное произведение А.*B=
4 2 6
3 8 3
3 2 3
матричное возведение в степень А^4=
412 464 544
232 264 308
544 616 724
поэлементное возведение в степень А.^4=
1 16 81
1 16 1
81 16 81
операция умножения обратной матрицы А на матрицу B: A\B=
-1.5000 0.0000 -0.5000
2.0000 2.7500 2.0000
0.5000 -1.5000 -0.5000
операция умножения А на обратную матрицу B: A/B=
-1.0000 -2.0000 11.0000
0 1.0000 -2.0000
0 -1.0000 6.0000
поэлементное деление А./B=
0.2500 2.0000 1.5000
0.3333 0.5000 0.3333
3.0000 2.0000 3.0000
поэлементное деление А.\B=
4.0000 0.5000 0.6667
3.0000 2.0000 3.0000
0.3333 0.5000 0.3333
операция умножения А на число 2: 2*A=
2 4 6
2 4 2
6 4 6
операция сложения матрицы А с числом 2: 2+A=
3 4 5
3 4 3
5 4 5
>>
Пример 3. Решить систему линейных алгебраических уравнений
Пример M-файла:
| A=[2 -7 10; 7 1 4; 1 -1 1] b=[-13; 11; 0] x=A\b |
Следует обратить внимание на то, что операция «деления» вектора b справа налево на матрицу А вызывает обращение матрицы А и умножение матрицы, обратной матрице А, на вектор b.
Получаемый результат:
A =
2 -7 10
7 1 4
1 -1 1
b =
-13
x =
-1
Варианты задания
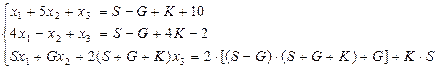
где
K =2, G - номер группы, S - номер студента по журналу.
Пример 4. Определить собственные значения и собственные векторы матрицы
Пример M-файла:
| A=[2 -1 0; -1 2 -1; 0 -1 2] [T,J]=eig(A) |
Получаемый результат:
A =
2 -1 0
-1 2 -1
0 -1 2
T =
0.5000 -0.7071 -0.5000
0.7071 0.0000 0.7071
0.5000 0.7071 -0.5000
J =
0.5858 0 0
0 2.0000 0
0 0 3.4142
Варианты задания
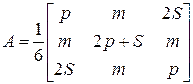
где
,
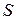– номер студента по списку в журнале, 
– номер группы.
Скалярное произведение двух векторов
, 
, 
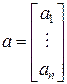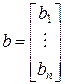
Варианты вычисления скалярного произведения в среде MATLAB:
s=sum(a.*b)=a’*b=dot(a,b)
Пример. Вычислить скалярное произведение 
,
где
; 
;
; 
; 
.
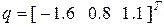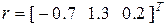Представим два способа.
| Первый вариант М-файла: | Второй вариант М-файла: |
| A=[1 2 3;1 2 1;3 2 0]; B=[4 1 2; 0 4 3;1 1 1]; p=[.1;1.7;-1.5]; q=[-1.6;0.8;1.1]; r=[-0.7;1.3;0.2]; s=(A*p)'* B*(q+r) | A=[1 2 3;1 2 1;3 2 0]; B=[4 1 2; 0 4 3;1 1 1]; p=[.1; 1.7; -1.5]; q=[-1.6; 0.8; 1.1]; r=[-0.7; 1.3; 0.2]; s=dot(A*p,B*(q+r)) |
|
|
|
Результат счета:
s =
33.1700
Варианты заданий.
| 1. | s= (Ap+q,q) | 13. | s= (q-ABq,q) | 25. | s= (B (r-q) ,p-r) |
| 2. | s= (Aq+p,Aq) | 14. | s= (A (p+r+q) ,p) | 26. | s= (Bq-Ar,Ar) |
| 3. | s= (B(p-r),r) | 15. | s= (B(r-q) ,p) | 27. | s= (B (r+q+r) ,AAp) |
| 4. | s= (Ar,Bp) | 16. | s= (A (q-p) ,p) | 28. | s= (A (p+q+r),AAr) |
| 5. | s= (Aq-Bp,r) | 17. | s= (B(q-p-r) ,q) | 29. | s= (B (r-p) ,BBr) |
| 6. | s= (AAp,q) | 18. | s= (ABp-r,q) | 30. | s= (BBr,Aq) |
| 7. | s= (Aq+AAq,q) | 19. | s= (Ar-Bq,p) | 31. | s= (Ap,B (q+r)) |
| 8. | s= (r+BBr,p) | 20. | s= (Ap,B(r-p)) | 32. | s= (BBq,r) |
| 9. | s= (Ap,Br) | 21. | s= (B (p-q) ,r) | 33. | s= (Ap-r,p+r) |
| 10. | s= (r,A (r-q)) | 22. | s= (AAp+q,p) | 34. | s= (BAp+q,p) |
| 11. | s= (q,Aq+Bp) | 23. | s= (Br-Ap,q-p) | 35. | s= (r+AAp,p) |
| 12. | S= (r+ABr,q) | 24. | s= (Ar+p,p+q) | 36. | s= (B (p-r-q) ,r) |
|
|
|
