V . Оптимальное регулирование параметров функционирования анализируемой системы, ситуационный анализ.

Рассмотрим пример. При анализе производительности мартеновских печей на одном из заводов исследовалась, в частности, зависимость между производительностью в тонно/часах и процентным содержанием углерода в металле по расплавлении ванны (пробу брали через час после первого скачивания шлака). Очевидно, величины производительности (y_i) и процентного содержания углерода (x_i) подвержены некоторому неконтролируемому разбросу, обусловленному влиянием множества не поддающихся строгому учету и контролю факторов.

Другими словами, последовательность пар чисел (x_i, y_i), i = 1, 2,..., 130, представляет в данном случае результаты 130 независимых наблюдений двумерной случайной величины (ξ, η). Здесь просматривается вполне определенная закономерность зависимости условного среднего значения производительности y_cp (x) = E (η | ξ = x) от величины процентного содержания углерода х. Поэтому, мы можем дать рекомендации технологу по оптимальному (с точки зрения максимизации производительности) управлению процессом выплавки: поддерживать процентное содержание углерода в пределах 0,6-1,0 %.

Основные типы зависимостей между количественными переменными:

Зависимость между неслучайными переменными. В этом случае результирующий показатель у детерминировано (однозначно) восстанавливается по значениям неслучайных объясняющих переменных Х = (x ⁽¹⁾, x ⁽²⁾,..., x ^{( p )})^Т, т. е. значения у зависят только от соответствующих значений Х и полностью ими определяются. Это – обычная схема чисто функциональной зависимости между неслучайными переменными, когда у является некоторой функцией от р переменных Х (т. е. y = f (X)), что является вырожденным случаем зависимостей вида 2.2, когда остаточная случайная компонента ε равна нулю (с вероятностью единица).

Регрессионная зависимость случайного результирующего показателя η от неслучайных объясняющих переменных Х. Природа такой связи может носить двойственный характер:

а) регистрация результирующего показателя η неизбежно связана с некоторыми ошибками измерения ε, в то время как предикторные (объясняющие) переменные Х = (x ⁽¹⁾, x ⁽²⁾,..., x ^{( p )})^Т измеряются без ошибок

б) значения результирующего показателя η зависят не только от соответствующих значений Х, но и еще от ряда неконтролируемых факторов, поэтому при каждом фиксированном значении Х’ соответствующие значения результирующего показателя η (Х’) = (η | X = X’) неизбежно подвержены некоторому случайному разбросу.

В этом случае объясняющие переменные Х играют роль неслучайного (векторного при р > 1) параметра, от которого зависит закон распределения вероятностей (в частности, среднее значение и дисперсия) исследуемого результирующего показателя η. Удобной математической моделью такого рода является разложение вида

η (Х) = f (X) + ε (X). (2.4)

Корреляционно-регрессионная зависимость между случайными векторами η – результирующим показателем и ξ – объясняющей переменной. Зависимости такого типа вообще характерны для описания хода технологических процессов, реальные значения параметров которых ξ = (ξ⁽¹⁾, ξ⁽²⁾,..., ξ^(р))^Т, равно как и характеризующие их результирующие показатели η = (η⁽¹⁾, η²⁾,..., η^(m))^Т, как правило, флюктуируют случайным (но взаимосвязанным) образом около установленных номиналов.

Зависимости структурного типа, или зависимости по схеме конфлюэнтного анализа. Конфлюэнтный анализ предоставляет совокупность методов математико-статистической обработки данных, относящихся к анализу априори постулируемых функциональных связей между количественными (случайными или неслучайными) переменными Y = (y ⁽¹⁾, y ⁽²⁾,..., y ^{( m )}) ^T и X = (x ⁽¹⁾, x ⁽²⁾,..., x ^{( p )}) ^T в условиях, когда наблюдаются не сами переменные, а случайные величины

_{, k = 1, 2,..., p ;} (2.5)

где и 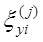- случайные ошибки измерений соответственно переменных х^{( k )} и y ^{( i )} в i-м наблюдении, a n - общее число наблюдений. [1].