 |
Вопрос 1. Понятие случайной величины
|
|
|
|
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И СПОСОБЫ ИХ ЗАДАНИЯ
|
Вопрос 1. Понятие случайной величины
Одним из важнейших понятий теории вероятностей является понятие случайной величины.
О.1.1. Случайной величиной (СВ) называется переменная величина, которая в результате испытания в зависимости от случая принимает одно (неизвестное заранее) значение из возможного множества своих значений.
Пример. Случайными величинами являются:
1. Число родившихся детей в городе в течение суток.
2. Дальность полета артиллерийского снаряда.
СВ обозначаются заглавными буквами латинского алфавита Х, У, Z…, а их возможные значения – соответствующими малыми буквами, т.е. 
(для Х), 
(для У) и т.п.
СВ делятся на два типа: дискретные и непрерывные.
О.1.2. Дискретной случайной величиной (ДСВ) называется случайная величина, которая принимает отдельные, изолированные друг от друга возможные значения с определенными вероятностями.
Число возможных значений дискретной случайной величины может быть конечным и бесконечным.
О.1.3. Непрерывной случайной величиной (НСВ) называется случайная величина, которая принимает все значения из некоторого конечного или бесконечного промежутка числовой оси.
Очевидно, что число возможных значений НСВ бесконечно.
Замечание
Сформулированное определение НСВ не является строгим. Строгое определение дадим позже.
В примере 1 первая СВ является дискретной, а вторая – непрерывной.
|
|
|
Вопрос 2. Дискретная случайная величина и способы ее задания
На первый взгляд может показаться, что для задания дискретной случайной величины достаточно перечислить все ее возможные значения. В действительности это не так: случайные величины могут иметь одинаковые перечни возможных значений, а вероятности их – различные. Поэтому знания только численных значений дискретной случайной величины не дает о ней полного представления. Необходимо знать вероятности возможных значений дискретной случайной величины. Это дает представление о том, как часто следует ожидать появление более выгодных или менее выгодных её значений, а этого достаточно для суждения об эффективности той операции, с которой связана данная случайная величина.
Таким образом, дискретная случайная величина считается заданной, если:
· перечислены все ее значения:
· известны вероятности этих значений.
В этом случае говорят, что задан закон распределения вероятностей дискретной случайной величины.
О.2.1. Законом распределения дискретной случайной величины называется соответствие между возможными значениями случайной величины и их вероятностями.
Закон распределения можно задать таблично, аналитически (в виде формулы) и графически.
Простейшей формой задания закона распределения ДСВ Х является таблица, в которой перечислены в порядке возрастания все возможные значения СВ 
и соответствующие им вероятности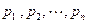 
: 
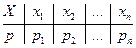
Такая таблица называется рядом распределения дискретной случайной величины.
Так как в одном испытании СВ 
принимает одно и только одно возможное значение, то события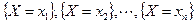 
образуют полную группу, а, следовательно, сумма вероятностей этих событий равна единице:
.
Ряд распределения может быть изображен графически в виде многоугольника или полигона распределения вероятностей, который представляет собой ломаную с вершинами 
, 
.
|
|
|
До сих пор в качестве исчерпывающего описания ДСВ мы рассматривали закон распределения, представляющий собой ряд распределения или формулу, позволяющую находить вероятности любых значений случайной величины. Однако такое описание СВ не является единственным, а, главное, не универсально. Так, оно неприменимо для непрерывной СВ, так как нельзя перечислить все бесконечное множество ее значений.
Рассмотрим другие способы задания случайных величин – с помощью интегральной и дифференциальной функций распределения.
|
|
|
