 |
Вопрос 3. Интегральная функция распределения и ее свойства
|
|
|
|
Наиболее универсальным способом описания СВ (и дискретных, и непрерывных) является использование функции распределения или интегральной функции распределения вероятностей.
Пусть Х – случайная величина, а 
— действительное число. Событие {Х < х} означает, что случайная величина Х приняла значение, меньшее х. Вероятность этого события, т.е. 
, зависит от х, т.е. является функцией от х.
О.3.1. Интегральной функцией распределения или просто функцией распределения случайной величины Х называется функция 
, определяющая для каждого значения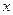 
вероятность того, что случайная величина 
примет значение, меньшее 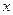, т. е. 
.
О.3.2. Случайная величина называется непрерывной, если ее интегральная функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
Свойства интегральной функции распределения
Свойство 1. Значения интегральной функции распределения принадлежат отрезку [0; 1], т.е.
.
Свойство 2. F(x) - неубывающая функция, т. е. 
при 
.
Следствие 1.
Вероятность того, что случайная величина Х примет значение, заключенное в полуинтервале 
, равна приращению интегральной функции на этом полуинтервале, т.е.
.
Следствие 2.
Вероятность того, что непрерывная СВ Х примет одно определенное значение х, равна нулю:
.
Из следствий 1 и 2 вытекает, что для непрерывной СВ Х справедливы равенства
.
Свойство 3.
Если возможные значения случайной величины Х принадлежат интервалу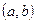 
, то
1) 
, 2) 
.
Следствие. Если возможные значения непрерывной случайной величины Х расположены на всей оси х, то справедливы следующие предельные соотношения: 
.
Интегральная функция распределения ДСВ
Зная ряд распределения ДСВ Х, можно построить функцию распределения этой СВ.
|
|
|
Функция распределения для ДСВ Х, которая принимает значения 
с вероятностями 
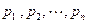, может быть найдена по формуле 
, где символ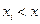 
означает, что суммируются вероятности тех значений, которые меньше х.
Графиком функции распределения ДСВ Х является ступенчатая фигура, имеющая в точках 
, 
, разрывы 1-го рода с соответствующей величиной скачка 
, .
Пример. Закон распределения ДСВ задан таблицей 
. Найти функцию распределения этой СВ.
Решение
: 
: 
: 
: 
: 
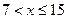Интегральная функция распределения: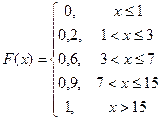 
Интегральная функция распределения – это универсальный способ задания любой СВ (и дискретной, и непрерывной), но не единственный.
Вопрос 4. Дифференциальная функция распределения и ее свойства
Задание непрерывной СВ с помощью интегральной функции распределения не является единственным. НСВ можно так же задать с помощью дифференциальной функции распределения или плотности распределения.
О.4.1. Дифференциальной функцией распределения или плотностью распределения непрерывной СВ Х называется функция 
,равная первой производной от интегральной функции распределения : 
.
Из определения 4.1. Þ интегральная функция является для дифференциальной функции первообразной.
Замечание
Для описания распределения вероятностей ДСВ плотность распределения неприменима.
С помощью дифференциальной функции распределения можно найти вероятность попадания непрерывной случайной величины в заданный интервал.
Т.4.1. Вероятность того, что непрерывная случайная величина Х примет значения, принадлежащие интервалу 
, равна определенному интегралу от ее плотности распределения, взятому в переделах от 
до 
: 
.
Свойства дифференциальной функции распределения
Свойство 1. 
- неотрицательная функция Þ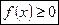 
.
Свойство 2. 
В частности, если все возможные значения СВ Х принадлежат интервалу 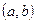, то 
.
|
|
|
|
|
|
