Обзор научных исследований в области теории принципов работы оптоволокна.

Оптоволоконные технологии (ОВТ) уже давно используются в различных областях техники, составляя основу не только средств передачи информации, но и разнообразных устройств измерения и контроля. В последнее десятилетие ОВТ все интенсивнее проникают в нефтяную и газовую промышленность, особенно в такие взаимосвязанные разделы этой отрасли, как сейсморазведка, бурение, геофизические исследования в скважинах и добыча нефти и газа. На основе ОВТ разработаны различные измерительные системы, которые, обладая высокой точностью, превосходят электронные устройства того же назначения в части стабильности и термостойкости. Измерительные элементы (сенсоры) таких систем не подвержены влиянию магнитных и электрических полей и стойки по отношению к вибрации и ударам. Кроме того, при измерениях, производимых на оптоволоконном каротажном кабеле, скважинная часть систем не требует электропитания и работает только с источниками света. [10]

Свет распространяется в сердцевине волокна, испытывая полное внутреннее отражение на границе с оболочкой. Он проникает в оболочку на глубину порядка длины волны, т.е. на глубину много меньше её толщины и, следовательно, не взаимодействует с покрытием из акрилатного лака. Это покрытие необходимо для защиты кварцевой оболочки от механических повреждений и воздействия воды. Волокна делятся на два основных типа: многомодовые и одномодовые. Для всех типов волокон, применяемых в линиях связи, диаметр кварцевой оболочки имеет стандартный размер 125+1 мкм. Номинальный диаметр сердцевины у многомодовых волокон 50 или 62.5 мкм. Диаметр сердцевины у одномодовых волокон может меняться в зависимости от типа волокна в пределах 7..9 мкм. Нормируемым параметром у одномодовых волокон является диаметр модового пятна, величина которого зависит от типа волокна и рабочей длины волны и лежит в пределах 8..10 мкм. Мода – это вид траектории, вдоль которой может распространяться свет.[5]

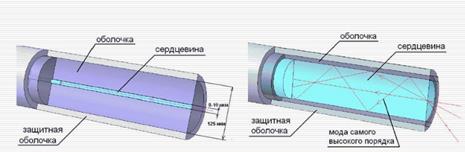
Рис. 2.1. Типы оптических волокон

Рассмотрим распространение света в волокне. Для того чтобы луч распространялся вдоль световода, он должен входить в него под углом не более некоторого критического относительно оси волокна, то есть попадать в воображаемый входной: конус.[5] Синус этого критического угла называется числовой апертурой световода NA и определяется через абсолютные показатели преломления слоев по формуле:

В многомодовом волокне показатели преломления сердцевины nc и оболочки n_об - различаются всего на 1-1,5 % (например, n_c: n_об = 1,515: 1,50). При этом апертура NA=0,2-0,3, и угол, под которым луч может войти в световод, не превышает 12-18° от оси. В одномодовом волокне показатели преломления различаются еще меньше (n_c: n_об = 1,505: 1,50), апертура NA=0,122 и угол не превышает 7° от оси. Чем больше апертура, тем легче ввести луч в волокно, по при этом увеличивается модовая дисперсия и сужается полоса пропускания (см. ниже). Числовая апертура характеризует все компоненты оптического канала — световоды, источники и приемники излучения. Для минимизации потерь энергии апертуры соединяемых элементов должны быть согласованными друг с другом.[6]

Рис. 2.2 Ввод света в оптоволокно: 1- входной конус; 2- осевая мода; 3- мода низкого порядка; 4- мода высокого порядка

Строго говоря, распространение сигнала в оптоволокне описывается уравнениями Максвелла. Возможные решения уравнении Максвелла соответствуют различным световым модам. В большинстве случаев можно пользоваться приближением геометрической оптики. Если рассматривать распространение сигнала с позиций геометрической оптики, то световые лучи, входящие под различными углами, будут распространяться по разным траекториям. Более высоким модам соответствуют лучи, входящие под большим углом, — они будут иметь большее число внутренних отражений по пути в световоде и будут проходить более длинный путь. Число мод для конкретного световода зависит от его конструкции — показателей преломления и диаметров сердцевины и оболочки — и длины волны.

Рис. 2.3 Распространение волн в световодах: а-в одномодовом; б- в многоводовом ступенчатым профилем; в- в многомодовом с градиентным профилем. 1-профиль показателся преломления, 2-вхдной импульс, 3- выходной импульс

 

Режим передачи — одномодовый или многомодовый — определяется способом ввода света в волокно (инжекции), конструкцией волокна и длиной волны источника. Ввод света для одномодового режима должен осуществляться узким лучом точно вдоль оси волокна, здесь в качестве источника можно использовать только лазер. [4] Для многомодовой передачи может использоваться и более дешевый светодиодный излучатель, имеющий более широкую диаграмму направленности. Передача в одномодовом режиме возможна лишь при длине волны, превышающей некоторое пороговое значение (cut-off wavelength). Эта пороговая длина волны определяется конструкцией волокна (диаметром сердцевины). Волокно для одномодовой передачи на длине волны 1300 нм имеет пороговую длину волны около 1200 мкм. Следовательно, в таком волокне на длине волны 850 нм одномодовая передача невозможна. При одномодовой передаче луч передается и по внутренней части оболочки, поэтому ее прозрачность, как и прозрачность сердцевины, влияет на затухание сигнала. Здесь световой л уч характеризуется диаметром модового пятна — области сечения волокна, через которую он распространяется (больше, чем сердцевина). В многомодовом волокне через оболочку свет не идет, так что ее прозрачность несущественна. [1]

В самом простом виде система волоконно-оптического распределенного измерения температуры состоит из оптического волокна в защитной трубке, источника лазерного излучения, оптического разветвителя, блока обработки оптоэлектронного сигнала и дисплея (рис.2.4).

Оптическое волокно — тонкое, как человеческий волос — всего лишь около 100 микрон в диаметре. Оно состоит из сердцевины диаметром от 5 до 50 микрон и оболочки, изготовленных из кварцевого стекла. Стекло сердцевины и оболочки имеет разный состав (например, из-за добавок других компонентов, таких как германий или фтор, в составе оболочки), чтобы различались показатели преломления и другие светодисперсионные характеристики.[10]

Рис. 2.4 Процесс волоконно-оптического распределенного измерения температуры.

Источник лазерного излучения посылает в сердцевину оптического волокна световые импульсы длительностью 10 нс (за это время каждый из них успевает пройти расстояние около 1 м). У сердцевины показатель преломления выше, чем у оболочки, и свет, отклонившийся от оси сердцевины, в конце концов попадает на ее границу с оболочкой под углом, величина которого обеспечивает его отражение обратно к оси сердцевины. Происходит так называемое полное внутреннее отражение. Однако в реальных оптических волокнах при прохождении импульса света часть его все же рассеивается. Свет может рассеиваться на флуктуациях плотности или состава стекла — по механизму, известному, как рэлеевское рассеяние, — или из-за акустических колебаний, изменяющих показатель преломления оптоволокна, — по механизму рассеяния Мандельштама–Бриллюэна. Самое сильное влияние на процесс волоконно-оптического распределенного измерения температуры оказывает третий из механизмов рассеяния света — комбинационное (рамановское) рассеяние, вызываемое неупругими (связанными с перераспределением энергии) столкновениями фотонов с молекулами в среде оптоволокна. Эти столкновения изменяют колебательную энергию молекул. Рассеянный фотон может либо отдать свою энергию молекуле, в результате чего она перейдет на более высокий колебательный уровень (стоксово рассеяние), либо принять энергию молекулы, и молекула перейдет на колебательный уровень ниже (антистоксово рассеяние).

Рис 2.5 Спектр обратного рассеяния.

 

Часть этого рассеянного света отражается обратно и возвращается по оптоволокну к источнику лазерного излучения. На этом пути сигнал обратного рассеяния отделяется от входящего импульса света направленным оптическим ответвителем. После этого отраженный сигнал посылается в высокочувствительное приемное устройство, где сигнал комбинационного рассеяния света отфильтровывается от доминирующего излучения обратного рэлеевского и бриллюэновского рассеяния.[12] Энергетический обмен между рассеивающейся молекулой и фотоном при комбинационном рассеянии зависит от температуры. Сигнал комбинационного рассеяния имеет две компоненты: стоксову и антистоксову. Стоксова компонента, длина волны которой больше, имеет очень слабую температурную зависимость, в отличие от антистоксовой компоненты обратного рассеяния с меньшей длиной волны, которая сильно зависит от температуры. Отношение этих двух компонент прямо пропорционально температуре рассеивающей среды. Кроме того, путем анализа излучения обратного рассеяния можно определить расстояние до места его возникновения в оптоволокне. Так как продолжительность каждого входящего импульса равна 10 нс, интервал, на котором произошло обратное рассеяние, точно соответствует одному из метровых отрезков оптоволокна. Следовательно, расчет профиля температуры по всей длине оптоволокна не требует ничего иного, кроме источника лазерного излучения, анализатора и знания исходной температуры в наземной части системы. В частности, нет необходимости в калибровке как отдельных точек по длине оптоволокна, так и всего оптоволокна перед его спуском.[10]

Оптическое волокно является частным случаем более общего понятия волновода. Рассмотрим суть круглого и двумерного вида волновода.

Двумерные волноводы с проходящими границами.

Далее рассмотрим волновод, заполненный однородной изотропной средой с действительной диэлектрической проницаемостью е и магнитной проницаемостью µ₀ (т. е. с магнитной проницаемостью свободного пространства). Сначала покажем, что обычная поперечная электромагнитная волна с плоской поляризацией (ТЕМ-волна) является решением задачи о двумерном волноводе с проводящими границами и поэтому задает моду волновода. Мода распространяется с хорошо определенными фазовой и групповой скоростями, поляризацией и распределением интенсивности по поперечному сечению. [7]

На языке микроволновой теории двумерный волновод с идеально проводящими границами следовало бы называть параллельной полосковой линией передач, пренебрегая при этом краевыми эффектами и эффектами, связанными с конечной величиной проводимости (с наличием скин-слоя). Наиболее подходящим в этом случае является подход, в основу которого положено описание с помощью уравнений Максвелла. Как будет показано, результаты, полученные при таком геометрическом подходе, совпадают с результатами, к которым приводит строгая электромагнитная теория.

параметров. [12]

Поперечные электромагнитные волны

Плоскополяризованная ТЕМ-волна в бесконечной диэлектрической среде.

Рассмотрим векторы электрического и магнитного полей в плоскополяризованной электромагнитной волне, распространяющейся в бесконечной изотропной среде. Для поперечной электромагнитной (ТЕМ) волны электрическое поле Е и магнитное поле Н образуют с направлением распространения, выбранным вдоль оси z, правую тройку векторов. Это изображено на рис. 2.6, где декартова система координат выбрана таким образом, чтобы

Е = (E_x,0,0), (2.2) Н = (0, Н_y, 0). (2.3)

При таком выборе системы координат систему уравнений Максвелла:

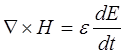, (2.4) 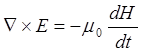, (2.5)

можно записать так:

0, = (2.6)

= (2.7)

Рис. 2.6 Взаимное расположение электрического и магнитного полей плоскополяризационной ТЕМ волны в неограниченной диэлектрической среде.	Рис. 2.7 Параллельные идеально проводящие плоскости, направляющие ТЕМ-моду.

Предположим, что компоненты поля Ех и Ну периодически зависят от времени t и координаты z, причем эта зависимость дается множителем ехр(іβz — iώt). Тогда уравнения (2.2.) и (2.3) принимают вид

и ,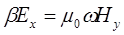

Т.е и следовательно, Е_x/Н_y=( /ɛ) (2.9)

Фазовая скорость: (2.10)

Вектор Пойнтинга: (2.11)

Усредненный по времени поток энергии: (2.12)

Параллельная полосковая линия передач

Рассмотрим распространение электромагнитной волны в среде, ограниченной двумя параллельными пластинами, которые предполагаются идеально проводящими. Предположим, что пластины, как показано на рис. 1.2, параллельны плоскости yz, расположены на расстоянии 2а друг от друга, имеют ширину d и бесконечную длину. (За расстояние между пластинами принята величина 2а для удобства при сравнении в дальнейшем с результатами, полученными для цилиндрических волноводов с радиусом а.) Электрическое и магнитное поля на поверхности каждой пластины должны удовлетворять следующим граничным условиям.[6]

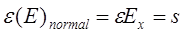(поверхностная плотность зарядов).

,

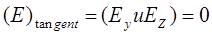(например) = К (ток/единица ширины).

Из этих уравнений видно, что ТЕМ-поля (Е_x, 0, 0), 0, Н_y, 0) удовлетворяют указанным граничным условиям. Полученные результаты можно суммировать следующим образом:

Ток в полоске =I=dK=dH_y, (2.13)

Напряжение между полосками =V=2aE_x, (2.14)

Характеристически

й импеданс

Мощность (2.15)

Действительно, нетрудно показать, что поля основных волн в линиях передач с произвольным поперечным сечением также описываются с помощью ТЕМ-мод. ТЕМ-волна не является единственной волной, которая может распространяться вдоль параллельной полосковой линии передач.

Уравнение Максвелла в круговых цилиндрических коорд инатах.

Из уравнений Максвелла в цилиндрических полярных координатах (r, θ, z) можно записать для однородной и изотропной среды, пренебрегая зависимостью от времени и координаты z, в виде

(2.32) 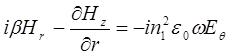, (2.33)

(2.34)

(2.35)

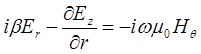, (2.36) (2.37)

Где n₁ –показатель преломления, E=(E_r, E_θ, E_z), H=(H_r, H_θ, H_z).

Найдем решения волнового уравнения, котоvрое можно записать в цилиндрических координатах в виде

(2.38)

где (г, θ) —либо E_z, либо Н_z. Так как рассматривается структура с круговой симметрией, будем искать решения, периодические по координате θ, т. е. решения вида

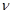( =0,1,2,…..). (2.39)

Подставляя выражение (2.39) в уравнение (2.40), получаем скалярное волновое уравнение для волноводов круглого сечения

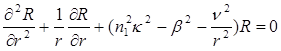(2.41)

Предполагая для каждой компоненты поля азимутальную периодичность вида (2.39), с помощью уравнений (2.32) — (2.37) поля можно записать через Е_z и Н_z:

(2.42)

(2.43)

(2.44)

(2.45)

где использованы обычные определения 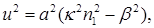. В общем случае продольные компоненты Е_z и Н_z можно найти, решив волновое уравнение (2.41). Это уравнение представляет собой хорошо известное дифференциальное уравнение для функций Бесселя; известно также, что существуют два независимых решения, которые следует выбирать в соответствии с граничными условиями. Чтобы получить осциллирующее решение в области г ≤ α, не имеющее особенности при г = 0, следует выбрать функцию Бесселя J_v(ur/a). При определении постоянных распространения β, ν

следует учитывать поляризацию волны. [8]

Теперь установим связь между постоянными распространения моды (β, ν) и направлением траектории луча (γ,α). Так как зависимость поля моды от координаты z имеет вид ехр(iβz) и в лучевой модели направление луча образует угол γ с осью z (рис. 2.8), имеем

(2.46)

Аналогично, поскольку направление луча образует угол α с тангенциальным направлением (рис. 2.9), азимутальную зависимость можно представить в виде exp[ . Сравнивая это выражение с азимутальной периодичностью в волновой модели, записанной в виде (2.39), находим

. (2.47)

Используя соотношение, связывающее θ₁, α, и γ (рис. 2.8) получаем

(2.48)

Физический смысл соотношений (2.46) — (2.47) можно понять на основе модели локальных плоских волн; на рис. 2.8 показано разложение волнового вектора на декартовы компоненты в точке r = α. Отметим, что такую интерпретацию можно получить из решения волнового уравнения
методом ВКБ, применив его в точке r = α.

Рис. 2.8. Разложение волнового вектора

в приближении локальных плоских

волн на радиальную, тангенциальную и

продольную компоненты при r = α.

 

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: