Расчет переходных процессов.

Для анализа переходного процесса предварительно следует привести схему к минимальному числу накопителей энергии, исключив параллельные и последовательные соединения однотипных реактивных элементов (индуктивностей или емкостей). Система интегродифференциальных уравнений, составленных в соответствии с законами Кирхгофа или методом контурных токов, может быть сведена путем подстановки к одному дифференциальному уравнению, которое используется для составления характеристического уравнения.

Порядок дифференциального, следовательно, и характеристического уравнения зависит от числа реактивных элементов приведенной схемы. Главная трудность в решения задачи классическим методом для уравнений высоких порядков состоит в отыскании корней характеристического уравнения и постоянных интегрирования. Поэтому для решения уравнений порядка выше второго применяют другие методы, в частности операторный метод, основанный на применении преобразования Лапласа и исключающий трудоемкую процедуру отыскания постоянных интегрирования.

Для практических целей при анализе переходных процессов в любой схеме классическим методом может быть рекомендован следующий алгоритм.

1. Рассчитать принужденный (установившийся) режим при t→∞. Определить принужденные токи и напряжения.

2. Рассчитать режим до коммутации. Определить токи в ветвях с индуктивностью и напряжения на конденсаторах. Значения этих величин в момент коммутации является независимыми начальными условиями.

3. Составить дифференциальные уравнения для свободного процесса (Е = 0) в схеме после коммутации по законам Кирхгофа или по методу контурных токов. Алгебраизировать данные уравнения, получить характеристическое уравнение и найти его корни. Существуют приемы, упрощающие операцию отыскания корней характеристического уравнения, например, приравнивание нулю входного операторного сопротивления цепи, которое получается путем замены в выражении комплексного сопротивления цепи множителя "jω" на оператор "р".

4. Записать общие выражения для искомых напряжений и токов в соответствии с видом корней характеристического уравнения.

5. Переписать величины, полученные в п. 4, и производные от них при t = 0.

6. Определить необходимые зависимые начальные условия, используя независимые начальные условия.

7. Подставив начальные условия в уравнения п. 5, найти постоянные интегрирования.

8. Записать законы изменения искомых токов и напряжений.

42. Переходные процессы в цепи постоянного тока с индуктивной катушкой.

Рассмотрим теперь электрическую цепь, содержащую катушку индуктивности (рисунок 5).

Пусть катушка обладает малым электрическим сопротивлением, меньшим, чем сопротивление резистора R. Внутренним сопротивлением источника тока пренебрежём. В момент времени t = 0 ключ К замыкается, и по цепи начинает протекать электрический ток. Если бы в цепи не было катушки индуктивности, то значение тока сразу бы установилось равным 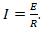. Из-за явления самоиндукции нарастание тока в катушке будет постепенным. При этом в катушке возникает ЭДС самоиндукции 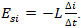. Здесь L — индуктивность катушки, — скорость изменения тока.

Так как резистор R и катушка L соединены последовательно, то E = U_R + U_L.

Но U_R = iR, а U_L = - E_si. Тогда

(6)

При малых изменениях тока за малые промежутки времени () дробь превращается в производную силы тока как функции времени . Тогда уравнение (6) превращается в дифференциальное уравнение

решение которого заключается в нахождении вида функции силы тока i(t) в катушке индуктивности от времени. Поступим так, как и в предыдущем случае. Представим уравнение (6) в виде

Время нарастания тока разобьём на малые одинаковые интервалы времени и посмотрим, как будет меняться его значение по истечении первого интервала от начала процесса, затем второго — и т.д. При этом, как уже было сказано,

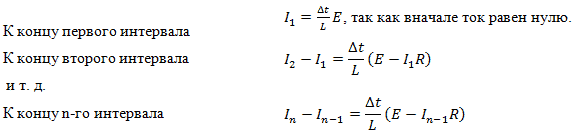
Несложное преобразование даёт следующее

(7)

Выражение (7) также является рекуррентным и позволит определить изменение значения силы тока в катушке индуктивности через одинаковые промежутки времени. При известных величинах E, R и L. Самостоятельно выведите формулы (8)

(8)

Можно также показать что при установившееся значение силы тока в цепи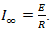

Обратим внимание, что в выражении (7) дробь безразмерна (докажите это).

Для определения количества интервалов времени n, а также самого интервала можно воспользоваться результатами предыдущего анализа. Время, за которое сила тока практически установится при точности амперметра, соответствующей

Пусть, например, E = 18В, R = 60Ом, L = 80Гн. Тогда T = 6,1с и при N = 100 имеем 0,061с. Эти данные соответствуют условию задания, приведённого в начале этой работы. Построим график, используя табличный процессор MS Excel (рисунке 6).

Красные маркеры поставлены в соответствии с таблицей к заданию, приведенному в начале работы. Как видно, теоретические расчёты хорошо согласуются с результатами измерений.

 

123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: