 |
Туннельный пробой в электронных компонентах. Методы определения
|
|
|
|
Рассмотрим зонную диаграмму диода с p-n переходом при обратном смещении при условии, что области эмиттера и базы диода легированы достаточно сильно (рис.2.1).

Рисунок 2.1 - Зонная диаграмма диода на базе сильнолегированного p-n перехода при обратном смещении.
Квантово-механическое рассмотрение туннельных переходов для электронов показывает, что в том случае, когда геометрическая ширина потенциального барьера сравнима с дебройлевской длиной волны электрона, возможны туннельные переходы электронов между заполненными и свободными состояниями, отделенными потенциальным барьером.
Форма потенциального барьера обусловлена полем p-n перехода. На рисунке 2.2 схематически изображен волновой пакет при туннелировании через потенциальный барьер треугольной формы.

Рисунок 2.2 - Схематическое изображение туннелирования волнового пакета через потенциальный барьер.
Возьмем уравнение Шредингера Hψ = Eψ, где H - гамильтониан для свободного электрона
 ,
,
Е - энергия электрона. Введем

Тогда снаружи от потенциального барьера уравнение Шредингера будет иметь вид:

Внутри потенциального барьера
 .
.
Решение для волновых функций электрона будем искать в следующем виде:

Используем условие непрерывности для волновой функции и ее производные ψ, dψ/dx на границах потенциального барьера, а также предположение об узком и глубоком потенциальном барьере (βW >> 1).
В этом случае для вероятности туннельного перехода Т получаем:

Выражение для туннельного тока электронов из зоны проводимости на свободные места в валентной зоне будет описываться следующим соотношением:
|
|
|

где использованы стандартные обозначения для функции распределения и плотности квантовых состояний.
При равновесных условиях на p+-n+ переходе токи слева и справа друг друга уравновешивают: IC→V = IV→C.
При подаче напряжения туннельные токи слева и справа друг друга уже не уравновешивают:

Здесь fC, fV - неравновесные функции распределения для электронов в зоне проводимости и валентной зоне.
Для барьера треугольной формы получено аналитическое выражение для зависимости туннельного тока Jтун от напряженности электрического поля Е следующего вида:

За напряженность электрического поля пробоя Eпр условно принимают такое значение поля Е, когда происходит десятикратное возрастание обратного тока стабилитрона: Iтун = 10·I0.
При этом для p-n переходов из различных полупроводников величина электрического поля пробоя Eпр составляет значения: кремний Si: Eпр = 4·105 В/см; германий Ge: Eпр = 2·105 В/см. Туннельный пробой в полупроводниках называют также зинеровским пробоем.
Оценим напряжение Uz, при котором происходит туннельный пробой. Будем считать, что величина поля пробоя Eпр определяется средним значением электрического поля в p-n переходе Eпр = Uобр/W. Поскольку ширина области пространственного заряда W зависит от напряжения по закону
 ,
,
то, приравнивая значения W из выражений
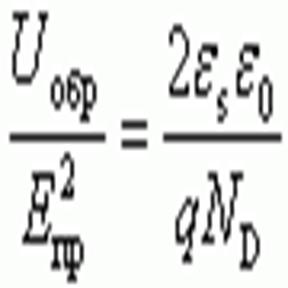 ,
,
получаем, что напряжение туннельного пробоя будет определяться следующим соотношением:

Рассмотрим, как зависит напряжение туннельного пробоя от удельного сопротивления базы стабилитрона. Поскольку легирующая концентрация в базе ND связана с удельным сопротивлением ρбазы соотношением ND = 1/ρμe, получаем:

Из уравнения (4.21) следует, что напряжение туннельного пробоя Uz возрастает с ростом сопротивления базы ρбазы.
Эмпирические зависимости напряжения туннельного пробоя Uz для различных полупроводников имеют следующий вид:
|
|
|
германий (Ge): Uz = 100ρn + 50ρp;
кремний (Si): Uz = 40ρn + 8ρp,
где n, p - удельные сопротивления n - и p-слоев, выраженные в (Ом·см).
|
|
|


