Алгоритм решения задачи минимизации времени выполнения комплекса работ

Рассмотрим метод решения задачи минимизации времени на приме­ре 10.3.

Пример 10.3.

Дана упорядоченная структурно-временная таблица 10.32 перечня работ по организации выставки-продажи товаров. Требуется построить сетевой график, определить критический путь, критические работы, ре­зервы времени, провести графический анализ комплекса работ и опти­мизацию сетевой модели по критерию минимума времени T при задан­ных ресурсах В. Определить экономию. Построить оптимальный сетевой план работ.

Анализ сетевой модели. Чтобы провести анализ сетевой модели, а за­тем ее оптимизацию, необходимо определить основные характеристики СМ. Эти характеристики определим двумя способами: аналитически с помощью формул и результаты вычислений заносим в таблицу 10.32 и графически — построением сетевого моделирования.

Табличный способ моделирования. Графы (колонки) 1,2 и 3 таблицы 10.33 заполняем на основании исходных данных таблицы 10.32. В графе 4 заполняем ранние сроки начала работ, определяемые с графика, путем выбора максимального из сроков раннего окончания предшествующих работ. Количество сравниваемых сроков равно количеству предшествую­щих работ графы 2. Заполнение графы 5 производится суммированием значений граф 3 и 4, т.е. раннее окончание каждой работы определяется сложением величин раннего начала и продолжительности работы.

После заполнения граф 4 и 5 определяется критический путь, равный максимально раннему сроку окончания работ, т.е. Т = 29 часам.

Значение критического пути заносится в последнюю сроку графы 7 и заполнение ее ведется снизу вверх. Время каждой работы определяется как разность между поздним окончанием работ и их продолжительно­стью. Наименьшее значение записывается в графу 7.

Значения графы 6 получаются вычислением данных графы 7 и значе­ний колонки 3.

Значения графы 8 — полный резерв времени, равный разности вели­чин колонок 6 и 4 или 7 и 5. Если r_n(i,k) равен нулю, то работа является критической.

В графу 10 резерв времени событий записывается величина, равная разности между поздним событием окончания работы, заканчивающим­ся событием к графы 7, и ранним началом работы, начинающимся собы­тием к, т.е. значения 10графа = 7графа — Зграфа (но не по строкам).

Значения свободного резерва времени работы rce(i,k) вычисляются как разность значений граф 10 и 8. Величины графы 9 указывают на ре­зервы работ, необходимые для оптимизации модели.

В графе 11 записаны значения коэффициента напряженности, вычис­ленные по формуле (10.31).

Графический способ решения задачи сетевого моделирования. Решим задачу графическим способом, построив сетевую модель по данным таб­лицы 10.32. и выполнив ее оптимизацию.

Решение.

Построим сетевую модель по данным структурно-временной таб­лицы 10.32, указывая события: начальное — 1 и конечное — 11, работы a₁÷a₁₃ и соответствующие им длительности.

Укажем пути на сетевом графике (последовательность работ, со­единяющая начальное и конечное событие) рассматриваемой модели (4 пути):

1 путь: a₁, а₅, а₆, а₉, а₁₁, а₁₂, а₁₃ — содержит 7 работ;

2 путь: a₁, а₃, а₄, а₇, а₉, а₁₁, а₁₂, а₁₃ — содержит 8 работ;

3 путь: a₁, а₃, а₄, а₈, а₁₀, а₁₁, а₁₂, а₁₃ — содержит 8 работ;

4 путь: а₂, а₁₀, а₁₁, а₁₂, а₁₃ — содержит 5 работ.

Работы (i,k)	Количест­во пред­шествую­щих работ	Время работ (i,k)	Сроки выполнения работ	Резервы времени	Kн
Ранние	Поздние	Работ	собы­тий Rk
Начала t р.н (i,k)	Окончания t р.о (i,k)	Начала t п.н (i,k)	Окончания t п.о (i,k)	полный rп(i,k)	свобод­ный rс(i,k)
				5 = (3) + (4)	6 = (7)-(3)	7	8 = (6) - (4), или (7-5)
а1 (1,2)
a2 (1,7)										0,68
a3 (2,4)
a 4(4,5)
as, (2,3)										0,64
a 6,(3,6)										0,64
a7 (5,6)
a 8.(5,7)
a 9,(6,8)
а10. (7,8)
а11 (8,9)
а12 (9,10)
а13 (10,11)

 

 

Рис. 10.48

М: 1 см = 2 ч

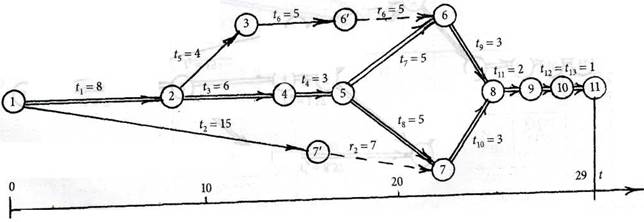Рис. 10.49

Рис. 10.50

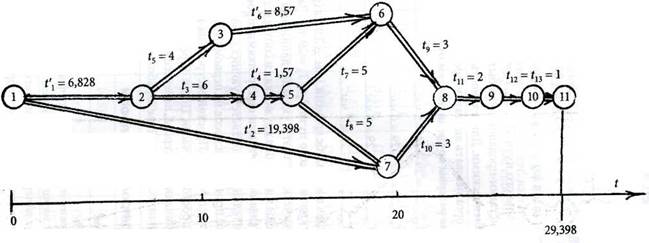
Рис. 10.51

3. Определим длительность пути во времени, подставляя соответст­вующие значения работ:

Т₁ = 8 + 4 + 5 + 3 + 2+1 + 1= 24 час;

Т₂ = 8 + 6 + 3 + 5 + 3 + 2+1 + 1= 29 час;

Т ₃ = 8 + 6 + 3 + 5 + 3 + 2+1 + 1= 29 час;

Т ₄ = 15 + 3 + 2 + 1 + 1 = 22 час.

Длительность максимального пути Т₂ = 29, Т ₃ = 29. За это время все работы по организации выставки-продажи могут быть выполнены. То есть пути Т ₂ и Т₃ являются критическими. Длительность минимального пути Т₄ = 22 часа. За это время организовать выставку-продажу не получится.

4. Определяем полные резервы времени по всем путям:

Т_{к p}_ Т_{1 =} 29-24 = 5 час;

Т_кр_Т₂ = 29-29 = 0 час;

Т_кр_Т₃ = 29-29 = 0 час;

Т_кр_Т₄ = 29-22 = 7час

5. Строим сетевой график в масштабе времени 1 см — 2 часа (рис. 10.49), построение начинается с критического пути Т₂ = Т₃ = 29 час. Затем стро­им остальные пути. Критические работы указаны двойными линиями (дугами). События отмечены цифрами в кружочках и соответствуют вер­шинам графа, а работы указаны отрезками со стрелками, проекции ко­торых на ось ot равны длительности соответствующих работ.

Из рис. 10.49 видно, что простой ресурсов на первом пути происходит на работе а₆, а время простоя t₆ = 5 час. Простой ресурсов на 4 пути проис­ходит на работе а₂, время простоя — 7 часов. После определения работ, на которых происходит простаивание ресурсов, перенесем на часть ресурсов с этих работ на работы критических путей, т.е. с работы а₆ на работу а₄.

Контрольные вопросы

1. Что называется графом?

2. Разновидности графов.

3. Какими способами можно представлять графы?

4. В чем отличие путей и маршрутов в орграфах?

5. Какие графы называют эйлеровыми и гамильтоновыми?

6. Какие задачи торговли решают с помощью теории графов?

ЗАДАЧИ

Задачи 10.(1-6)

Для заданного графа G = (Х,17) аналитически построить орграф, со­ставить матрицы: смежности — А, инциденции — В, пропускных способ­ностей дуг — Си достижимости — D.

Найти максимальный стационарный поток и минимальный разрез в орсети G = (X,U), заданной списком дуг, из источника 1 в 7 строк при за­данной функции с: пропускных способностей дуг и при заданном начальном потоке f₀.

 

Варианты
№	Uik Cik	Uik Cik	Uik Cik	Uik Cik	Uik Cik	Uik Cik
	(1,2) 9	(1,2) 8	(1,2) 3	(1,2) 4	(1,2) 11	(1,2) 12
	(1,3) 7	(1,3) 6	(1,3) 4	(1,3) 6	(1,3) 10	(1,6) 11
	(2,3) 5	(1,4) 4	(2,3) 5	(2,3) 8	(1,4) 9	(2,3) 10
	(3,2) 3	(3,2) 2	(3,2) 6	(3,2) 2	(1,5) 8	(3,2) 7
	(1,4) 4	(2,3) 9	(2,4) 2	(2,4) 7	(2,3) 7	(2,4) 8
	(4,2) 2	(2,5) 7	(2,5) 8	(2,5) 5	(3,2) 6	(2,6) 9
	(2,5) 6	(3,4) 5	(3,5) 6	(5,2) 9	(2,6) 4	(4,3) 5
	(3,4) 2	(4,3) 4	(3,6) 4	(3,6) 3	(4,3) 5	(3,4) 3
	(4,3) 1	(3,5) 3	(6,3) 7	(6,3) 1	(3,4) 1	(3,7) 4
	(3,6) 3	(3,6) 2	(4,5) 9	(3,4) 2	(3,6) 3	(5,4) 6
	(4,5) 4	(4,7) 6	(5,4) 5	(4,5) 3	(6,3) 2	(4,5) 2
	(4,7) 6	(6,4) 4	(4,7) 3	(4,7) 4	(4,7) 5	(4,7) 5
	(6,4) 5	(6,5) 8	(6,5) 2	(6,5) 5	(5,4) 6	(6,5) 3
	(5,6) 7	(5,6) 7	(5,6) 1	(5,6) 3	(5,6) 7	(5,6) 4
	(5,7) 8	(5,7) 6	(5,7) 7	(5,7) 6	(5,7) 9	(5,7) 9
	(6,7) 9	(6,7) 8	(6,7) 8	(6,7) 7	(6,7) 8	(6,7) 6

 

 

Задачи 10. (7-11)

Дана структурно-временная таблица комплекса работ по организа­ции выставки-продажи товаров. Требуется построить сетевой график, определить критические пути, критические работы, резервы времени, провести графический анализ комплекса работ и оптимизацию сетевой модели по критерию минимума времени T при заданных ресурсах В. Определить экономию. Построить оптимальный сетевой план работ.

 

№	Содержание работ	Обозначение, аi	Опорные работы	Коэффициенты перерасчета, Сi/b	Длительность работы в часах
Значения ti,	Варианты
	Заказ на оборудо­вание и товары	a1	-	C1 = 0,1	t1
	Разработка системы учета спроса	а2	-	С2 = 0,1	t2
	Отбор товаров, выписка счетов	a3	a1	С3 = 0,3	t3
	Завоз товаров	а4	a3	С4 = 0,4	t4
	Завоз оборудо­вания	a5	a1	С5 = 0,5	t5
	установка обору­дования	а6	a3	С6 = 0,6	t6
	Выкладка товара	а7	a4	С7 = 0,7	t7
	Учет товара	а8	a8	C8 = 0,8	t8				.8
	Оформление зала, витрины	а9	а6а7	С9 = 0,9	t9
	Изучение доку­ментов учета	a10	а2а8	С10 = 1,0	t10
	Репетиция вы­ставки-продажи	a11	а9а10	С11 = 0,1	t11
	Проведение выставки	a12	a11	С12 = 0,1	t12
	Анализ результа­тов	a13	a11	С13 = 0,1	t13

Задачи 10. (12-13)

Требуется назначить четырех работников A_j5 i = (1,4) на четыре соот­ветствующие должности В_к, к = (1,4) из условия максимума продажи то­варов, если матрица имеет вид:

12)

	B1	B2	B3	B4
A1
А2
А3
А4

13)

	B1	B2	B3	B4
A1
А2
А3
А4

Задачи 11. (14-15)

Три торговых предприятия А; доставляют грузы четырем оптовым базам В_к, расстояния между которыми заданы в таблицах. Определить из каких предприятий и на какие оптовые базы направить грузы, чтобы суммарные расстояния были минимальными.

14)

	B1	B2	B3	B4
A1
А2
А3

 

15)

	B1	B2	B3	B4
A1
А2
А3

 

 

12	Поделиться:

Воспользуйтесь поиском по сайту: