 |
Переходные процессы в цепях I порядка
|
|
|
|
Рассмотрим примеры расчета переходных процессов в неразветвленных электрических цепях, с достаточной степенью наглядности иллюстрирующие физические явления, происходящие в них в переходных режимах.
4.2.5.1. Разряд заряженной ёмкости через сопротивление R
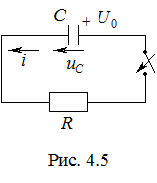1. Запишем правило коммутации для цепи на рис. 4.5:
.
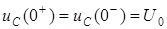2. Составим дифференциальное уравнение цепи:
;
.
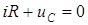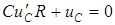Характеристическое уравнение первого порядка:
,
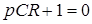корень которого 
.
3. Полное решение дифференциального уравнения:
.
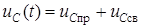Поскольку уравнение имеет первый порядок, свободная составляющая имеет одну экспоненту
.
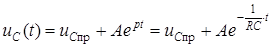4. Определим принужденную составляющую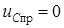 
.
5. Для определения постоянной интегрирования A запишем полное решение для момента t = 0+
.
Применив правило коммутации, получим окончательное решение
.
Ток в цепи определяется с помощью дифференциального закона Ома
,
, 
.
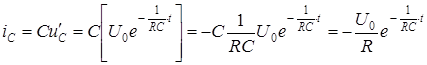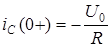Итак, имеем две экспоненты, описывающие изменения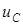 
и 
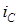. Графики изменения 
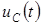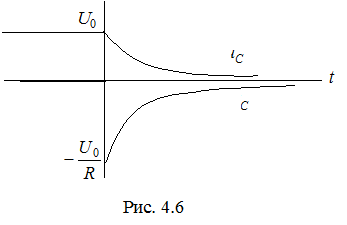
и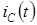 
представлены на рис. 4.6. Напряжение на конденсаторе непрерывно в момент коммутации и уменьшается по экспоненциальному закону от начального значения U 0. Знак «минус» в выражении для тока говорит о том, что ток при разряде конденсатора направлен противоположно току при его заряде. В начальный момент значение тока максимально, его спад связан с уменьшением напряжения на элементах цепи. Ток на ёмкости меняется скачком.
Введём величину, характеризующую скорость изменения электрической величины в переходном режиме, называемую постоянная времени (t).
Величина 
показывает, за какой промежуток времени свободная составляющая переходного процесса уменьшается в 
раз.
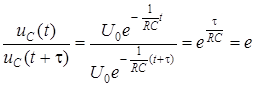Чем больше , тем медленнее переходный процесс, тем больше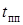 
. Хотя полученные выше выражения определяют бесконечную длительность переходного процесса – свободные составляющие лишь асимптотически стремятся к нулю – практически можно считать, что переходный процесс заканчивается за время, равное 
.
|
|
|
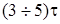Постоянную времени можно графически определить по длине подкасательной, проведённой в любой точке свободной составляющей переходного процесса (рис. 4.7).
Постоянная времени измеряется в секундах и для цепей первого порядка связана с корнем характеристического уравнения
. (4.10)
Рассмотрим энергетические соотношения, описывающие работу цепи после коммутации.
Энергия электрического поля конденсатора до коммутации – 
, в результате полного разряда при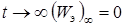 
.
Покажем, что вся энергия, запасенная в конденсаторе, выделяется в виде тепловой энергии на резисторе R:
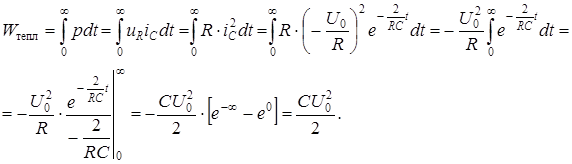
4.2.5.2. Подключение R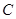 
-цепи к источнику постоянного напряжения
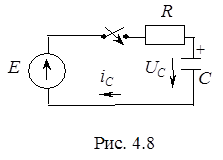1. Запишем правило коммутации для цепи на рис. 4.8
.
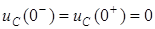2. Получим дифференциальное уравнение цепи
,
, 
,
.
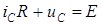Характеристическое уравнение цепи
,
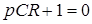корень которого
.
Постоянная времени 
.
3. Запишем полное решение
.
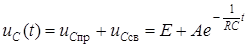Здесь свободная составляющая также включает только одну экспоненту, поскольку цепь имеет первый порядок.
4. Подставив в полное решение t = 0+, определим постоянную интегрирования на основании правил коммутации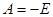 
.
Таким образом, окончательный результат имеет вид
.
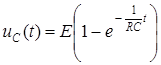Ток в цепи
.
Графики изменения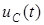 
и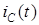 
представлены на рис. 4.9. Значение тока, содержащее лишь свободную составляющую, максимально в начальный момент времени, когда оно скачком достигает значение 
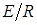, и все напряжение источника приложено к резистору. По мере зарядки конденсатора напряжение на нем повышается, что ведет к соответственному уменьшению тока в цепи.
4.2.5.3. Подключение R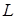 
-цепи к источнику постоянного напряжения
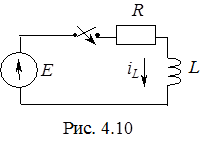1. Запишем правило коммутации для цепи на рис. 4.10
.
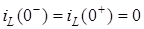2. Получим дифференциальное уравнение цепи
|
|
|
,
,
характеристическое уравнение
.
Корень характеристического уравнения и постоянная времени соответственно
, 
.
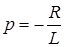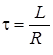3. Полное решение имеет вид:
.
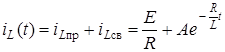4. Подставив в iL (t) t = 0+ на основании правила коммутации определим постоянную интегрирования
.
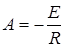Таким образом,
.
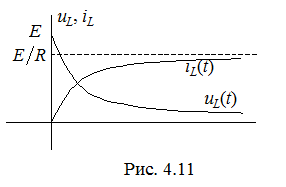
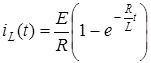Напряжение на индуктивности
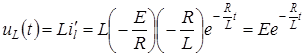. Графики изменения uL (t), iL (t) приведены на рис. 4.11.
4.2.5.4. Подключение RC -цепи к источнику гармонического напряжения
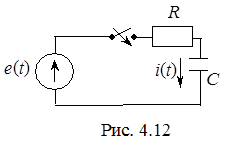
Рассмотрим случай, когда в цепи (рис. 4.12) действует источник синусоидальной ЭДС
.
Здесь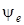 
– фаза включения, т.к. она определяется моментом срабатывания коммутатора. Интуитивно следует ожидать влияние 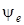на качественную и количественную картину протекания переходного процесса.
Порядок расчета переходных процессов, описанный выше, не претерпевает никаких изменений.
1. Запишем правило коммутации
.
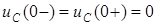2. Дифференциальное уравнение и соответствующее ему характеристическое уравнение:
.
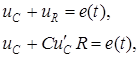
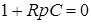Корень характеристического уравнения
.
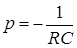3. Полное решение для рассматриваемой цепи первого порядка
.
4. Расчет принужденной составляющей произведем символическим методом
;
;
;
.
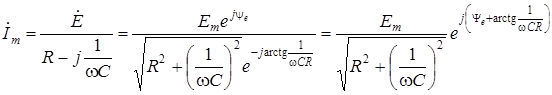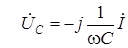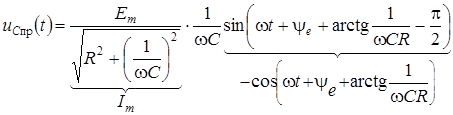5. Для расчета постоянной интегрирования запишем полное решение для момента t = 0+
;
.
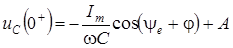В соответствии с правилом коммутации
;
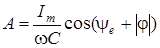Таким образом,
или
.
Определим
;
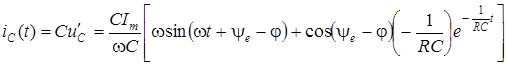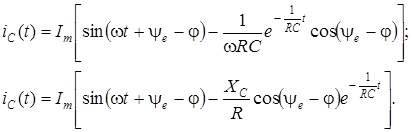
Оба выражения для uC и iC в общем случае имеют периодическую принужденную и апериодическую свободную составляющие. При этом характер переходного процесса существенно зависит от двух факторов – начальной фазы напряжения источника в момент включения 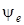и соотношения параметров цепи 
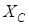и R.
Исследуем ожидаемое влияние фазы включения 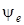источника на переходный режим
1) Пусть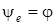 
, тогда 
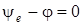. Поскольку cos 0 = 1, получим
. 
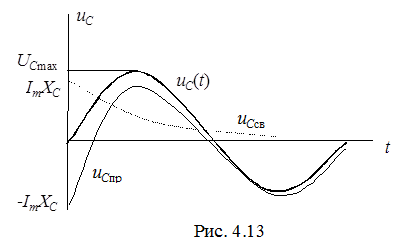
а) исследование кривой напряжения (рис. 4.13) наглядно демонстрирует, что максимальное напряжение в переходном режиме ограничено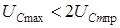 
.
б) исследование кривой тока (рис. 4.14).
Максимальное значение тока в переходном режиме зависит от соотношения 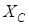и R и может превышать Im пр в несколько раз. Однако этот начальный всплеск тока является кратковременным.
 |
2) В случае, если
, поскольку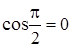 
, получим
 |
Таким образом, в данном случае в цепи переходный процесс не наблюдается.
|
|
|
