 |
Матричные и векторные нормы. Спектральный радиус его связь с матричными нормами.
|
|
|
|
Матричные нормы. Свойства матричных норм.
Норма матрицы может быть введена различными способами.
Способ 1. Рассматривая прямоугольные m×n -матрицы как вектора в m × n -мерном пространстве, можно определить норму матрицы как норму соответствующего вектора. При таком подходе для матрицы A = (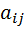
), i = 
, j = 
вводятся три основные нормы:
= 
-- октаэдрическая
= 
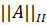² -- сферическая
= 
max 
-- 
- норма
Остальные нормы называют вспомогательными.
Способ 2. Рассмотрим произвольную m×n -матрицу A с элементами из поля P, где P = C или P = R. Матрице A соответствует линейный оператор y = A x (4. 4. 1) из пространства 
в пространство 
. Если в пространствах и выбраны некоторые базисы 
, 
,..., 
и 
, 
,..., 
соответственно, то линейный оператор y = A x будет иметь m × n -матрицу A = (A , A ,..., A ).
На линейный оператор y = A x можно смотреть как на матричное равенство, где x = 
и y =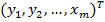 
— вектора-столбцы координат векторов x и y соответственно в выбранных базисах. Более подробно
= 
+ 
+ ... + 
= 
+ 
+ ... + 
.............................
= 
+ 
+ ... + 
.
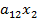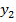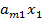Таким образом, если в пространствах 
и 
фиксированы некоторыебазисы, то между m×n -матрицами и линейными операторами A: → устанавливается взаимно однозначное соответствие. Поэтому нормой матрицы можно считать норму соответствующего линейного оператора. Вспоминая определение нормы линейного оператора, приходим к следующему определению.
Определение 4.4.1. Нормой прямоугольной m × n -матрицы A называется число ||A|| =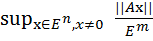 
= 
,(4. 4. 1) где || · || 
, || · || 
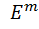— нормы векторов в пространствах и 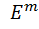соответственно. Как видно из определения норма m×n -матрицы A определяется как самой матрицей, так и теми векторными нормами, которые выбраны в пространствах и 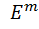. При изменении этих норм изменяется и норма матрицы.
|
|
|
С целью сокращения записи в дальнейшем не будем указывать какому из пространств E n или E m относится векторная норма. Тогда равенство (4.4.1) перепишется как ||A|| = 
= 
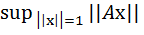. (4. 4. 2)
Свойство 1. ||A|| ≥ 0, причем ||A|| = 0 тогда и только тогда, когда A = 0.
Д о к а з а т е л ь с т в о. Из (4.4.2) видно, что ||A|| ≥ 0. Пусть A = 0, тогда ∀ x ∈ выполнится A x = 0, значит, ||A x || = 0, откуда с учетом (4.4.2) ||A|| = 0. Обратно, пусть ||A|| = 0, тогда из (4.4.2) ||A x || = 0 ∀ x ≠ 0. Но, очевидно, ||A 0 || = 0. Итак, ||A x || = 0 ∀ x, откуда A = 0.
Свойство 2. ||λA|| = |λ| ||A|| ∀ λ ∈ P. (напомним, что P = C или P = R).
Д о к а з а т е л ь с т в о. В силу (4.4.2) ||λA|| = 
= 
= |λ|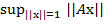 
= |λ| ||A||.
Свойство 3. ||A + B|| ≤ ||A|| + ||B||.
Д о к а з а т е л ь с т в о. При определении нормы матрицы (4.4.2)
||A + B|| = 
≤ 
≤ 
= ||A|| + ||B||
Свойство 4. ||A x || ≤ ||A|| · || x ||.
Д о к а з а т е л ь с т в о. По свойствам точной верхней грани из определения 4.4.1 следует, что для x ≠ 0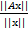 
≤ ||A||, т.е. для x 
0 действительно выполняется ||A x || ≤ ||A|| · || x ||. Если же x = 0, то A x = 0, т.е. ||A x || = 0 и || x || = 0, т.е. доказываемое неравенство также выполняется.
Свойство 5. Если p × n-матрица B: → 
, а m × p-матрица A: → 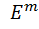, то ||AB|| ≤ ||A|| · ||B||.
Д о к а з а т е л ь с т в о. В самом деле, пользуясь свойством 4, получим ||AB|| = 
≤ 
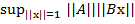= ||A|| = ||A|| · ||B||.
Связь матричных и векторных норм.
Определение. Матричная норма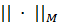 
и векторная норма 
называются согласованными между собой, если 
≤ 
· 
.
Очевидно, что матричная норма "операторного" определения y = A x согласована с векторной нормой, фигурирующей в этом определении. Для любой векторной нормы всегда существует матричная норма, согласованная с ней (например, матричная норма из определения y = A x). Обратно, для любой матричной нормы существует согласованная с ней векторная норма. Достаточно взять ту же норму у вектора, которая бралась у матрицы (ведь вектор — это матрица размера n × 1). Тогда эти нормы согласованы в силу определения матричной нормой. Итак, справедлива следующая
|
|
|
Теорема 4.4.1 (Люстерник). Для любой векторной нормы существует согласованная с ней матричная норма, а для любой матричной нормы существует согласованная с ней векторная норма. Отметим, что основные матричные нормы 
, 
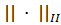, || · ||∞ не совпадают с матричными нормами, согласованными с векторными нормами , , || · ||∞.
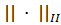Матричные и векторные нормы. Спектральный радиус его связь с матричными нормами.
Определение 4.4.4. Матричные нормы 
и 
называются эквивалентными, если существуют постоянные β ≥ α > 0 такие, что для любой матрицы α 
≤ 
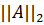≤ β . То, что это отношение эквивалентности, доказывается точно так же, как и для векторных норм. Каким бы способом ни была введена матричная норма, она может в конечном счете рассматриваться как норма вектора в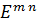 
, поскольку при любом подходе будут выполняться аксиомы нормы вектора. Поэтому из теоремы Люстерника о том, что все нормы на евклидовом пространстве эквивалентны между собой, вытекает теорема (Люстерник). Любые две матричные нормы эквивалентны. Когда рассматривалась сходимость последовательности матриц, она определялась как покоординатная сходимость. Так как такая сходимость эквивалентна сходимости по сферической норме, а по теореме 4.4.2 сходимость по сферической норме эквивалентна сходимости по любой матричной норме, то в определении сходимости последовательности матрицмо жет быть взята любая матричная норма. Рассмотрим специфические свойства некоторых матричных норм.
Определение 4.4.5. Если 
, 
,..., 
— все собственные значения квадратной матрицы A, то число R = max(| |, | 
|,..., | |) называется спектральным радиусом матрицы A.
Свойство. Матричная норма квадратной матрицы не меньше ее спектрального радиуса.
Д о к а з а т е л ь с т в о. В силу теоремы о том, что в комплексном пространстве V всякое линейное преобразование A имеет хотя бы один собственный вектор. для любой квадратной матрицы существует собственный вектор. Пусть x — собственный вектор A, соответствующий собственному значению λ: A x = λ x, x ≠ 0. По теореме о том, для любой матричной нормы существует согласованная с ней векторная норма. Выберем ее. Тогда 
= 
= 
≤ 
. Так как x ≠ 0, то 
> 0. Поэтому 
≥ |λ|. Так как это неравенство выполняется для всех собственных значений, то ≥ R.
|
|
|
26.+ Локализационные круги.
|
|
|
