 |
Локализация собственных значений. Круги Гершгорина.
|
|
|
|
Пусть A = (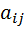 ) — произвольная квадратная матрица n -го порядка и λ — некоторое ее собственное значение. Тогда |A−λE| = 0, т.е. A−λE —вырожденная матрица. Следовательно для нее не могут выполняться все условия Адамара, т.е. должно иметь место хотя бы одно из неравенств |λ −
) — произвольная квадратная матрица n -го порядка и λ — некоторое ее собственное значение. Тогда |A−λE| = 0, т.е. A−λE —вырожденная матрица. Следовательно для нее не могут выполняться все условия Адамара, т.е. должно иметь место хотя бы одно из неравенств |λ −  | ≤
| ≤  , i =
, i =  . Каждое из неравенств |λ −
. Каждое из неравенств |λ −  | ≤
| ≤  , i =
, i =  определяет некоторый круг в комплексной λ -плоскости радиуса
определяет некоторый круг в комплексной λ -плоскости радиуса  с центром в точке
с центром в точке 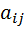 , называемый кругом Гершгорина. Поэтому справедлива теорема Гершгорина. Каждое собственное значение λ матрицы A = (
, называемый кругом Гершгорина. Поэтому справедлива теорема Гершгорина. Каждое собственное значение λ матрицы A = (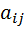 ) всегда расположено в одном из кругов |λ −
) всегда расположено в одном из кругов |λ −  | ≤
| ≤  , i =
, i =  .
.
Таким образом, объединение всех кругов Гершгорина дает некоторую область локализации собственных значений матрицы A, т.е. область, в которой заведомо лежат все собственные значения матрицы A. Каждый критерий регулярности приводит к своей области локализации собственных значений. Так, например, исходя из условий
Адамара для столбцов, мы получим область локализации в виде объединения n кругов
|λ −  | ≤
| ≤  , i =
, i =  .
.
27.+ Произведение треугольных матриц.
Говорят, что матрица имеет треугольный вид, если все ее элементы, расположенные выше или ниже главной диагонали, равны нулю:
 или
или 
Верхняя треугольная матрица и нижняя треугольная матрица.
Треугольные матрицы обладают следующими свойствами:
1. Сумма треугольных матриц одного наименования есть треугольная матрица того же наименования; при этом диагональные элементы матриц складываются.
2. Произведение треугольных матриц одного наименования есть треугольная матрица того же наименования.
3. При возведении треугольной матрицы в целую положительную степень ее диагональные элементы возводятся в эту же самую степень.
|
|
|
4. При умножении треугольной матрицы на некоторое число ее диагональные элементы умножаются на это же самое число
Можно ли разложить квадратную матрицу в произведение двух
треугольных? Допустим, что
( ) = (
) = (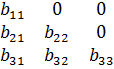 ) (
) ( )
)
Приравнивая соответствующие элементы этого равенства получим:
 =
=  , a 12 = b 11 c 12, a 13 = b 11 c 13,
, a 12 = b 11 c 12, a 13 = b 11 c 13,
a 21 = b 21 c 11, a 22 = b 21 c 12 + b 22 c 22, a 23 = b 21 c 13 + b 22 c 23,
a 31 = b 31 c 31, a 32 = b 31 c 12 + b 32 c 22, a 33 = b 31 c 13 + b 32 c 23 + b 33 c 33,
откуда, предполагая, что b 11 c 11 b 22 c 22 ≠ 0 получим
 =
=  ,
, 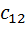 =
=  ,
,  =
=  ,
,  =
=  ,
,  =
=  ,
,  =
=  ,
,
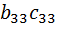 =
= 



 ,
,  =
=  ,
,  =
= 
Отсюда видно, что задавая произвольным образом b 11 ≠ 0, b 22 ≠ 0, мы однозначно выразим все элементы матриц в правой части (5.1.1) через элементы матрицы A, кроме b 33 и c 33, которые задаем произвольно, лишь бы b 33 c 33 = a 33 −b 31 c 13 −b 32 c 23. Итак, если b 11 c 11 b 22 c 22 ≠ 0, то справедливо разложение (5.1.1). Какие условия надо наложить, чтобы b 11 c 11 b 22 c 22 ≠0? Так как a 11 ≠0 тогда и только тогда, когда b 11 c 11 ≠0, то остается посмотреть, когда b 22 c 22 ≠0. Обозначим  =
=  ,
,  = (
= ( ).
).
Введем аналогичные обозначения для матриц B и C. Если (5.1.1) выполняются, то нетрудно видеть, что A 2 = B 2 C 2. Но тогда |A 2 | = |B 2 ||C 2 | = b 11 b 22 c 11 c 22. Поэтому, если |A 1 |  0, |A 2 |
0, |A 2 |  0, то b 11 b 22 c 11 c 22 ≠ 0. Итак, справедлива теорема 5.1.1. Если
0, то b 11 b 22 c 11 c 22 ≠ 0. Итак, справедлива теорема 5.1.1. Если  ≠ 0,
≠ 0,  ≠ 0, то справедливо разложение (5.1.1).
≠ 0, то справедливо разложение (5.1.1).
Эта теорема легко обобщается на матрицы любого порядка.
Теорема 5.1.2. Какова бы ни была квадратная матрица A = (aij) порядка n с отличными от нуля главными минорами
 ≠ 0,
≠ 0,  ≠ 0,...,
≠ 0,..., 
ее всегда можно разложить в произведение A = BC ˙, (5. 1. 2) где B и C — соответственно левая и правая треугольные матрицы.
До к а з а т е л ь с т в о. Заметим, что если разложение (5.1.2) существует, то оно будет заведомо не единственным. В самом деле, запишем (5.1.2) в следующем виде:
A – BD  C, где D — диагональная матрица. Тогда матрицы BD и
C, где D — диагональная матрица. Тогда матрицы BD и  C будут снова треугольными прежнего строения. Покажем теперь, что матричное уравнение (5.1.2) имеет решение. Пусть
C будут снова треугольными прежнего строения. Покажем теперь, что матричное уравнение (5.1.2) имеет решение. Пусть  и
и  — элементы матриц B и C. Приравнивая между собой элементы матрицы A и произведения BC, получаем
— элементы матриц B и C. Приравнивая между собой элементы матрицы A и произведения BC, получаем  =
=  . Отсюда следует: b 11 c 11 = a 11; b 11 c 11 = a 11; c 1 j =
. Отсюда следует: b 11 c 11 = a 11; b 11 c 11 = a 11; c 1 j =  , bi 1 =
, bi 1 =  , j = 2, 3 ,..., n;
, j = 2, 3 ,..., n;  =
=  −
−  , i = 2, 3 ,..., n, cij =
, i = 2, 3 ,..., n, cij =  , bji =
, bji =  , i =2,3,...,n, j = i +1, i +2 ,..., n. (5.1.3)
, i =2,3,...,n, j = i +1, i +2 ,..., n. (5.1.3)
|
|
|
Итак, уравнение (5.1.2) будет наверняка иметь решение, если все числа bii и cii (i = 1, 2 ,..., n − 1) не равны нулю. Предположим, что  = 0 при некотором k. Из (5.1.3) вытекает, что в этом случае возможно осуществить лишь разложение
= 0 при некотором k. Из (5.1.3) вытекает, что в этом случае возможно осуществить лишь разложение  =
=  ,
,
где  ,
,  , — матрицы угловых миноров k -го порядка матриц A, B и C. Далее находим |
, — матрицы угловых миноров k -го порядка матриц A, B и C. Далее находим |  | = |
| = |  |˙|
|˙|  | =
| =  =0. Это противоречит предположению теоремы, следовательно, все числа
=0. Это противоречит предположению теоремы, следовательно, все числа  и
и  (i = 1, 2 ,..., n− 1) не равны нулю и разложение (5.1.2) имеет место.
(i = 1, 2 ,..., n− 1) не равны нулю и разложение (5.1.2) имеет место.
28.+ Унитарные матрицы. Примеры. Свойства.
Матрица A с элементами из поля комплексных чисел C называется унитарной, если она удовлетворяет уравнению  = E, где A* — матрица, сопряженная с A, т.е. A* =
= E, где A* — матрица, сопряженная с A, т.е. A* =  , черта означает операцию комплексного сопряжения, T — операция транспонирования матрицы. Если унитарная матрица является вещественной, то наше определение превращается в определение ортогональной матрицы. Таким образом, унитарность — обобщение ортогональности на случай матрицс комплексными элементами. Соотношение
, черта означает операцию комплексного сопряжения, T — операция транспонирования матрицы. Если унитарная матрица является вещественной, то наше определение превращается в определение ортогональной матрицы. Таким образом, унитарность — обобщение ортогональности на случай матрицс комплексными элементами. Соотношение  = E можно переписать в виде
= E можно переписать в виде  =
=  , i,k = 1, 2 ,..., n, где
, i,k = 1, 2 ,..., n, где  — символ Кронекера. Если обозначить i -ю строку матрицы A через
— символ Кронекера. Если обозначить i -ю строку матрицы A через 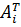 (i =
(i =  ), то через скалярное произведение последнее соотношение запишется как (
), то через скалярное произведение последнее соотношение запишется как (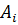 ,
,  )=
)= 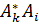 =
=  .
.
Таким образом, унитарная матрица — это такая матрица, у которой
строки ортогональны и каждая строка имеет единичную длину. Из равенства  = E следует, что A* =
= E следует, что A* =  , поэтому A*A =
, поэтому A*A =  A = E. Следовательно,
A = E. Следовательно,
 =
=  , i,k = 1, 2 ,..., n.
, i,k = 1, 2 ,..., n.
Это означает, что столбцы матрицы A ортогональны, а каждый столбец
имеет единичную длину.
Унитарные матрицы обладают следующими свойствами.
1. Если A — унитарная матрица, то ее определитель есть комплексное число, по модулю равное единице. Действительно, det ( ) = det (A) detA* = det (A) det (
) = det (A) detA* = det (A) det ( ) = (det (A))² = 1, откуда |det (A) | = 1 (здесь для определителя матрицы A использовано обозначение det (A), чтобы не спутать с обозначением модуля числа).
) = (det (A))² = 1, откуда |det (A) | = 1 (здесь для определителя матрицы A использовано обозначение det (A), чтобы не спутать с обозначением модуля числа).
2. Если A — унитарная матрица, то A* =  . Это утверждение вытекает непосредственно из раенства
. Это утверждение вытекает непосредственно из раенства  = E после умножения обеих его частей слева на
= E после умножения обеих его частей слева на  .
.
3. Если A — унитарная матрица, то A* тоже унитарна.
|
|
|
4. Произведение двух унитарных матрице есть матрица унитарная. В
самом деле, если A и B — унитарные, то (AB)(AB) * = ABB* A* = AEA* = E.
5. Унитарная матрица порядка n имеет n взаимно ортогональных собственных векторов с характеристическими числами, по модулю равными единице.
29.+Эрмитовы матрицы. Примеры. Свойства.
Матрица A называется эрмитовой, если она удовлетворяет равенству
A =  . Эти матрицы характеризуются такими соотношениями между элементами:
. Эти матрицы характеризуются такими соотношениями между элементами:
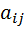 =
=  (5. 4. 1) Матрицы отражения являются эрмитовыми, так как
(5. 4. 1) Матрицы отражения являются эрмитовыми, так как 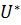 =
=  ∗ = E − 2
∗ = E − 2  = E − 2 w
= E − 2 w  = U.
= U.
Эрмитовы матрицы обладают следующими свойствами.
1. Если A — эрмитова, то ее определитель — действительное число.
Действительно, |A| = |  | = |
| = |  | = |
| = |  | =
| =  .
.
2. Если A эрмитова, то A− 1 также эрмитова. В самом деле,  =
= 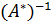 =
=  .
.
3. Произведение двух перестановочных эрмитовых матриц является эрмитовой матрицей. Действительно, если A и B эрмитовы и AB = BA, то AB = BA =  = (
= ( .
.
4. Если матрица A эрмитова, то любая унитарно ей подобная матрица также эрмитова. В самом деле, пусть B = 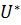 AU, где U — унитарная матрица. Тогда
AU, где U — унитарная матрица. Тогда  =
= 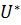 A
A  =
= 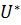 AU = B.
AU = B.
5. Эрмитова матрица порядка n имеет n взаимно ортогональных собственных векторов с действительными собственными значениями.
Для любой квадратной матрицы A и любых векторов-столбцов x и y (A x, y) =  A x =
A x =  x = (x,
x = (x,  y).
y).
В случае, когда матрица A эрмитова, это дает (A x, y) = (x, A y). Полагая y = x, получим
(A x, x) = (x, A x) =  .
.
Таким образом, для эрмитовой матрицы скалярное произведение (A x, x) есть действительное число. Среди эрмитовых матрицособое место занимают положительно
определенные матрицы.
Определение 5.4.1. Эрмитова матрица A называется положительно определенной, если скалярное произведение (A x, x) > 0 для любого вектора x ≠ 0.
Ввиду того, что (A x, x) =  A x =
A x = 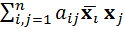 есть комплексная квадратичная форма от переменных
есть комплексная квадратичная форма от переменных  ,
,  ,...,
,...,  с матрицей A, то эрмитова матрица с матрицей A является
с матрицей A, то эрмитова матрица с матрицей A является
положительно определенной тогда и только тогда, когда положительно
определенной является квадратичная форма с матрицей A, т.е. когда для любых комплексных чисел  ,
,  ,...,
,...,  , не равных нулю одновременно,
, не равных нулю одновременно, 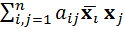 > 0.
> 0.
Собственные значения положительно определенной матрицы строго положительны.
|
|
|
Действительно, пусть u — собственный вектор матрицы A, соответствующий собственному значению λ, т.е. A u = λ u, причем u ≠ 0. Так как A положительно определена и u ≠ 0, то (A u, u) = (λ u, u) = λ (u, u) > 0. Поскольку для u ≠ 0 выполняется (u, u) =  > 0, то из последнего неравенства следует, что λ > 0. Матрицы вида
> 0, то из последнего неравенства следует, что λ > 0. Матрицы вида
A =  B, где B — прямоугольная матрица с линейно независимыми столбцами,
B, где B — прямоугольная матрица с линейно независимыми столбцами,
являются положительно определенными.
30. + Критерии регулярности и поляризация собственных значений.
Пусть A = ( ) — произвольная квадратная матрица порядка n с
) — произвольная квадратная матрица порядка n с
комплексными элементами. Допустим, что эта матрица вырождена, т.е.
|A| = 0. Тогда столбцы матрицы линейно зависимы, т.е. существуют
числа  ,
,  ,...,
,...,  , не равные нулю одновременно такие, что линейная комбинация этих векторов равна нулю:
, не равные нулю одновременно такие, что линейная комбинация этих векторов равна нулю:
т.е. 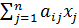 = 0, i =
= 0, i = 
Пусть k ∈ { 1, 2 ,..., n} таково, что |  | = max {|
| = max {|  |, |
|, |  |,..., |
|,..., |  |}. Так
|}. Так
как не все  = 0, то |
= 0, то |  | > 0. Для выбранного k, в частности,
| > 0. Для выбранного k, в частности,  = 0. Но тогда
= 0. Но тогда
|  ||
||  | = |
| = |  | ≤
| ≤  ≤
≤ 
 . Сокращая на
. Сокращая на  , получаем
, получаем
|  |≤
|≤  (6. 1. 1). Поэтому, если выполняются условия Адамара |
(6. 1. 1). Поэтому, если выполняются условия Адамара | 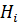 |
|  |
|  |
| 
 > 0 i =
> 0 i =  , (6. 1. 2) то неравенство |
, (6. 1. 2) то неравенство |  |≤
|≤  невозможно и, следовательно, матрица A является регулярной (невырожденной), т.е. |A| ≠ 0.
невозможно и, следовательно, матрица A является регулярной (невырожденной), т.е. |A| ≠ 0.
Таким образом, справедлива теорема Адамара. Если для квадратной матрицы n-го порядка выполняются n неравенств | 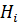 |
|  |
|  |
| 
 > 0 i =
> 0 i =  , то матрица A является невырожденной. Условие
, то матрица A является невырожденной. Условие 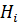 > 0 означает, что модуль диагонального элемента
> 0 означает, что модуль диагонального элемента  строго больше суммы модулей всех остальных элементов i -й строки. Такой элемент называется доминирующим для своей строки. Условие Адамара требует, чтобы все диагональные элементы матрицы A были доминирующими для своих строк.
строго больше суммы модулей всех остальных элементов i -й строки. Такой элемент называется доминирующим для своей строки. Условие Адамара требует, чтобы все диагональные элементы матрицы A были доминирующими для своих строк.
Теорема 6.1.2. Если выполняются условия Адамара | 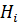 |
|  |
|  |
| 
 > 0 i =
> 0 i =  , то для модуля определителя A справедлива следующая оценка снизу: mod|A| ≥
, то для модуля определителя A справедлива следующая оценка снизу: mod|A| ≥  ...
... 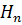 > 0. (6. 1. 3)
> 0. (6. 1. 3)
Д о к а з а т е л ь с т в о. Введем вспомогательную матрицу F = ( ), где
), где  =
=  , i,j =
, i,j =  для которой |
для которой |  −
−  =
=  (
(  −
−  i =
i =  .(6. 1. 4) Пусть
.(6. 1. 4) Пусть  — собственное значение этой матрицы, которому соответствует собственный вектор x =
— собственное значение этой матрицы, которому соответствует собственный вектор x =  . Пусть k таково, что |
. Пусть k таково, что |  | = max {|
| = max {|  |, |
|, |  |,..., |
|,..., |  }, причем |
}, причем |  | > 0. Тогда F x =
| > 0. Тогда F x =  x. Приравнивая k -ю координату, получим
x. Приравнивая k -ю координату, получим 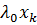 =
=  . Из этого равенства с учетом соотношений (6.1.4) получаем
. Из этого равенства с учетом соотношений (6.1.4) получаем
|  ||
||  | = |
| = | 
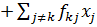 |
|  |
|  |
|  |
|  |
| 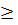 |
|  |
|  |
|  |
|  | (
| (  |) = |
|) = |  |. Сокращая на |
|. Сокращая на |  |, найдем |
|, найдем |  | ≥ 1.
| ≥ 1.
Но определитель |F| равен произведению собственных значений матрицы F. Каждое из них по модулю больше или равно единицы. Поэтому и mod|F| ≥ 1. (6. 1. 5) С другой стороны, |F| =  . (6. 1. 6) Подставляя (6.1.6) в неравенство (6.1.5), получим искомое неравенство (6.1.3). Отметим, что для класса матриц, удовлетворяющих условиям
. (6. 1. 6) Подставляя (6.1.6) в неравенство (6.1.5), получим искомое неравенство (6.1.3). Отметим, что для класса матриц, удовлетворяющих условиям
Адамара с заданными значениями  ...
... 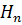 , оценка (6.1.3) не улучшаема, поскольку при A = (
, оценка (6.1.3) не улучшаема, поскольку при A = ( ) неравенство (6.1.3) превращается в равенство.
) неравенство (6.1.3) превращается в равенство.
|
|
|
Замечание 6.1.1. Так как |A| = |  |, то заменяя матрицу A транспонированной матрицей
|, то заменяя матрицу A транспонированной матрицей  , получаем достаточные условия невырожденности матрицы A в виде условий Адамара для столбцов
, получаем достаточные условия невырожденности матрицы A в виде условий Адамара для столбцов 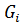 ≡
≡  −
−  > 0, i =
> 0, i =  . (6. 1. 7) При выполнении этих условий вместо (6.1.3) получится оценка mod|A| ≥
. (6. 1. 7) При выполнении этих условий вместо (6.1.3) получится оценка mod|A| ≥ 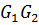 ...
...  . (6. 1. 8)
. (6. 1. 8)
Пусть C — произвольная невырожденная квадратная матрица n -го порядка. Тогда матрицы A и AC одновременно являются невырожденными. Поэтому в условиях (6.1.2), (6.1.7), а также в оценках (6.1.3), (6.1.8) можно матрицу A заменить на матрицу AC. Варьируя матрицу C, будем получать различные (не эквивалентные между собой) достаточные условия невырожденности, а также оценки для |A|, аналогичные (6.1.3)
и (6.1.8). В частности, с помощью подбора надлежащей матрицы C можно осуществить произвольную перестановку столбцов. Тогда вместо условий (6.1.2) получим условия
 =
= 
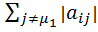 > 0, i =
> 0, i =  , где (
, где (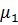 ,
,  ,...,
,...,  ) — фиксированная, но произвольная перестановка индексов 1, 2 ,..., n. Итак, справедлива теорема. Матрица A = (
) — фиксированная, но произвольная перестановка индексов 1, 2 ,..., n. Итак, справедлива теорема. Матрица A = ( ) является невырожденной, если в каждой ее строке имеется доминирующий (не обязательно диагональный) элемент и эти n доминирующих элементов расположены
) является невырожденной, если в каждой ее строке имеется доминирующий (не обязательно диагональный) элемент и эти n доминирующих элементов расположены
в различных столбцах. Аналогичный результат имеет место для столбцов
31.Матричные уравнения AX=XB.
Рассмотрим матричное уравнение AX = XB, где А и В -- заданные матрицы
(вообще говоря, разных порядков), X – искомая прямоугольная матрица:
A 
 , B
, B 
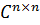 , X
, X 
 ,
,
Рассмотрим элементарные делители(в поле С) матрицы А:
 ,
,  ,...,
,...,  ,
,  +...+
+...+  = m
= m
И элементарные делители(в поле С) матрицы В:
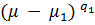 ,
,  ,...,
,...,  ,
,  +...+
+...+ 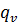 = n
= n
Через 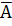 и
и  обозначим жордановы нормальные формы матриц А и В, а через U и V -- соответствующие матрицы перехода:
обозначим жордановы нормальные формы матриц А и В, а через U и V -- соответствующие матрицы перехода:
A = U 
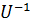 , B = V
, B = V 
 .
.
Тогда:
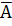 = diag{
= diag{ 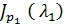 ,...,
,...,  },
},  +
+  +...+
+...+  = m,
= m,
 = diag{
= diag{  ,...,
,...,  },
},  +
+ 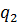 +...+
+...+ 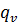 = n
= n
Здесь

 +
+  =[
=[ 
 ]
]
-- жардановы клетки матрицы А,


 =
= 
 -- единичная матрица,
-- единичная матрица,

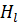 =
= 
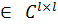 -- нильпотентная клетка Жордана порядка l.
-- нильпотентная клетка Жордана порядка l.


Теорема. Общее решение уравнения AX=XB, где A  ,
, 
A = U 
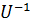 , B = V
, B = V 
 .
.
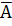 = diag{
= diag{ 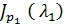 ,...,
,...,  },
},  +
+  +...+
+...+  = m,
= m,
 = diag{
= diag{  ,...,
,...,  },
},  +
+ 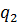 +...+
+...+ 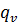 = n,
= n,
может быть найдено по формуле
X = U 
Здесь  -- общее решение уравнения
-- общее решение уравнения
 =
= 
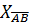 = [
= [  ],
], 

 ,
,  =
= 
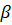 =
=  .
.
Если  , то
, то  = 0,
= 0,  , то
, то  произвольная правильная верхняя треугольная матрица.
произвольная правильная верхняя треугольная матрица.
Матрица X зависит о т N произвольных параметров 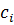 :
:
X =  , где N =
, где N = 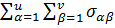 ,
,  = deg НОД
= deg НОД  ,
,  },
},
 =
= 
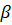 =
=  .
.
Заметим, что  которое получатся из X, если параметру
которое получатся из X, если параметру 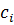 присвоить значение единица, а остальным -- нуль, является частным решением уравнения 3.1. Для ненулевого решения X частные решения
присвоить значение единица, а остальным -- нуль, является частным решением уравнения 3.1. Для ненулевого решения X частные решения  линейно независимы и образуют фундаментальную систему решений. Действительно, если это не так, тогда сущствует неотрицательная линейная комбинация
линейно независимы и образуют фундаментальную систему решений. Действительно, если это не так, тогда сущствует неотрицательная линейная комбинация  то есть при ненулевых значения параметра
то есть при ненулевых значения параметра 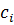 матрица X, а значит, и
матрица X, а значит, и 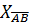 равны нулю, что невозможно.
равны нулю, что невозможно.
Следствие. Если матрицы А и В не имеют одинаковых собственных значений, то уравнене AX=XB имеет только нулевое решение, то есть X=0.
32.Матричные уравнения AX−XB = С
Пусть дано уравнение AX−XB = С, где A 
 , B
, B 
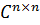 , C
, C 
 , X
, X 
 ,
,
Это матричное уравнение эквивалентно системе m*n линейных уравнений относительно элементов матрицы X.
Рассмотрим соответствующее однородное уравнение AX−XB =0. Из теоремы об общем решении уравнения AX−XB = С следует, что если матрицы A и B не имеют одинаковых собственных значений, то уравнение AX−XB = 0 имеет только нулевое решение, а значит AX−XB = С имеет единственное решение. Если же матрицы А и В имеют одинаковые значения, то в зависимости от С возможны два варианта:
1) Уравнение не имеет решения.
2) X =  +
+  , где
, где  -- произвольное частное решение уравнения AX−XB = С,
-- произвольное частное решение уравнения AX−XB = С,
а  -- общее решение уравнения AX−XB = 0.
-- общее решение уравнения AX−XB = 0.
|
|
|


