Механические воздействия и их характеристики

 

При эксплуатации и транспортировке РЭСИ подвергаются механическим воздействиям: вибрационным, ударным и линейным нагрузкам, а также звуковому давлению (акустическим шумам). К изделиям, предназначенным для функционирования в условиях воздействия механических нагрузок, предъявляют требования по прочности и устойчивости при воздействии этих нагрузок. К изделиям, не предназначенным для функционирования в условиях воздействия механических нагрузок, предъявляют требования только по прочности при воздействии этих нагрузок. Уровни вибрационных воздействий показаны на рисунке 1.4.

 

Рисунок 3 — Уровни вибрационных воздействий, которым подвергаются РЭСИ:

1 — вибрация; 2 — вибрация, возбуждаемая ударом

Вибрация — один из самых опасных и наиболее часто встречающихся на практике видов механических воздействий. В общем случае под вибрацией понимают, колебания самого изделия или каких-либо частей его конструкции. Вибрации приводят к поломкам конструкции, обрывам проводов и кабелей, нарушению герметичности, к механическим напряжениям и деформациям в РЭСИ. Наиболее часто вибрационные нагрузки возникают на самолетах и ракетах.

Механическая прочность, необходимая для нормального функционирования РЭСИ во время и после воздействия на них различных вибрационных нагрузок, должна быть заложена на этапе проектирования изделий. Для этого РЭСИ рассматривают как механические системы и применяют аналитические методы расчета их механических характеристик.

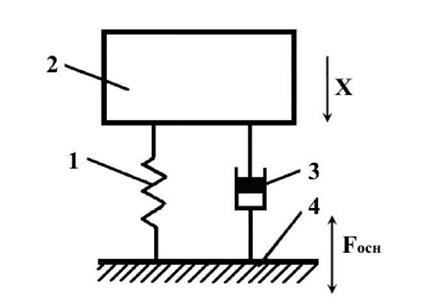
Далее приведен простой пример, когда изделие может быть представлено в виде механической колебательной системы с одной степенью свободы (рисунок 4)

 

Рисунок 4 — Схема линейного осцилятора с вязким трением:

1—пружина; 2—груз; 3— демпфер; 4 — стол вибростенда

 

Система состоит из груза массой m, пружины с жесткостью С и демпфера вязкого трения с коэффициентом демпфирования ŋ. Движение массы m от определяется изменением только одной координаты х под действием возбуждающей силы F _осн. Уравнение движения системы может быть получено на основе принципа Даламбера, согласно которому в каждый момент времени все силы, действующие на систему, находятся в равновесии, если в их число входит сила инерции. В общем случае дифференциальные уравнения движения любой колебательной механической системы могут быть составлены на основе уравнения Лагранжа в обобщенных координатах. На систему, изображенную на рисунке 4, действуют:

1) возбуждающая сила, приводящая к колебаниям опорного основания (например, стола вибростенда) с частотой со и амплитудой А;

F _осн = Asin (ω t), (6)

2)сила инерции Т _{x 2} (х₂ — ускорение); сила вязкого демпфирования ŋ _{x 1} (х₁ —скорость), пропорциональная мгновенной скорости массы и направленная в сторону, противоположную этой скорости;

3)сила упругости пружины С_х (х — координата центра масс груза). Уравнение движения массы m от относительно положения статического

равновесия имеет вид:

m_{x 2} +ŋ _x +С _x = A ∙ sin ∙ ωt. (7)

Разделив правую и левую части уравнения (1.3) на m после преобразования получим:

Х₂+2∙δ_о∙ω_о∙ x + ω²_о x =ω²_о∙ X_CT ∙ sin (ω t),(8)

где δ_о = ŋ/(2 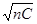) — параметр, пропорциональный коэффициенту демпфирования;

ω= 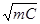—угловая частота собственных недемпфированных колебаний системы;

Х_ст=A/С — удлинение пружины, которое она получила бы под действием статической силы, равной амплитуде Л возбуждающей силы.

Решение уравнения (1.4) может быть представлено в виде суммы свободных и вынужденных колебаний:

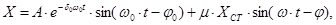  (9)

где φ₀ и φ — начальные фазы

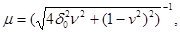 (0)

μ — коэффициент динамичности, показывающий, во сколько раз амплитуда вынужденных колебаний при действии возбуждающей силы вида (2) больше статического отклонения пружины;

v = ω / ω ₀ - безразмерный параметр, пропорциональный частоте возбуждающей силы.

Из первого слагаемого уравнения (5), представляющего выражение для свободных колебаний системы при наличии демпфирования, видно, что даже при малом значении δ_о множитель 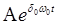 с течением времени t стремится к нулю и, следовательно, свободные колебания затухают.

Установившиеся вынужденные колебания определяются вторым слагаемым (5). Особенность этих колебаний состоит в том, что их амплитуда зависит не только от параметров системы и возбуждающей силы, но от частоты

со. При v = 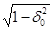  коэффициент динамичности максимален:

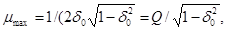(11)

где Q / 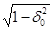 — добротность механической колебательной системы, зависящая

от количества энергии, рассеиваемой при вибрации.

Чем выше добротность, тем меньше затухание колебаний и тем острее пик резонансной кривой. Если частота со возбуждающей силы совпадает с собственной частотой со₀ механической системы без трения (δ₀=О, v = l), то происходит резонансное колебание. В этом случае нагрузки на РЭСИ возрастают в несколько раз. При нулевых начальных условиях (в отсутствие трения) уравнение для предельного случая резонансного состояния рассматриваемой системы принимает вид:

X 2=-(ω ₀ XcTicosω ₀ t)/2. (12)

Из формулы (8) видно, что амплитуда резонансных колебаний линейно зависит от времени t и частоты ω₀ собственных колебаний. При наличии трения в механической системе резонансный пик будет тем выше, чем большее время изделие находится в резонансном режиме и чем выше собственная частота конструкции.

Время достижения установившейся амплитуды резонансных колебаний реальных изделий измеряется, как правило, долями секунды. Ширина 2∆ f резонансной полосы частот определяется разностью частот f ˝ и f ´ (f ˝> f ´), при которых амплитуда А колебаний уменьшается до 0,7 своего значения при резонанс.

Так как

(13)

где f ₀ — резонансная частота, то

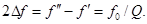(14)

Отсюда 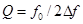(15)

Для расчета добротности изделия необходимо после настройки на резонанс измерить амплитуду колебаний, затем уменьшать частоту до тех пор, пока амплитуда колебаний не станет равной 0,7 амплитуды при резонансе. Полученная частота будет соответствовать частоте f '. Аналогичные действия следует провести, увеличивая частоту до значения f ". Тогда, вычислив 2Δ f по (9) и зная f ₀, можно по (10) найти добротность Q.

Удар. Ускорения, возникающие при резком изменении скорости или направления движения объекта, в котором применяются РЭСИ, вызывают механическое воздействие на них в виде удара. Вследствие удара возникают силы, деформирующие конструктивные элементы изделий и приводящие к образованию в них механических напряжений. Последние могут служить причиной разрушения изделий. Удар, как правило, сопровождается возбуждением затухающих колебаний, т.е. неустановившейся вибрацией на частотах собственных колебаний конструктивных элементов изделий. Уровни разрушающих усилий возрастают, если элементы конструкции резонируют на частотах возмущений, вызванных ударом. Если на РЭСИ действует серия ударов в виде импульсов, следующих один за другим, то возникающую вибрацию называют тряской.

Акустический шум. Особый интерес представляют так называемые баллистические волны, образующиеся от артиллерийских или реактивных снарядов, а также от самолетов, пролетающих через рассматриваемую среду со сверхзвуковой скоростью. Некоторые виды вибрации также сопровождаютсявыделением энергии звуковой частоты. Это явление принято называть акустическим шумом или акустической вибрацией.

Выделение энергии колебаний звуковой частоты сопровождается механическими колебаниями частиц среды воздуха, которые приводят к изменению давления по сравнению с атмосферным (статическим). Разность между статическим давлением и давлением в данной точке звукового поля называется звуковым давлением. Колебательное движение частиц среды при распространении звуковой волны характеризуется также колебательным смещением их от положения покоя. Скорость распространения звуковых волн в воздухе зависит в основном от температуры среды по закону . При нормальном атмосферном давлении р = 101300 Па и Т = 273 К (0°С) скорость звука равна 331 м/с. С повышением температуры до 290 К она увеличивается до 340 м/с.

На распространение звуковых волн в атмосфере большое влияние оказывают ее неоднородности. При этом скорость звука зависит не только от температуры воздуха, но и от его влажности, а также направления и силы ветра.

 

1234	Поделиться:

Воспользуйтесь поиском по сайту: