 |
Определение полной дизъюнкции n переменных. Определение СКНФ
|
|
|
|
Двузначная логика
Определение функции двузначной логики от n переменных и число всех функций от n переменных
Функция двузначной логики – закон, который любому упорядоченному набору нулей и единиц (x1..xn) где любой x Î{0,1} ставит в соответствие некоторое вполне определённое число 0 или 1. Число всех функций от n переменных 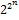
Определение соседних наборов.
Наборы называются соседними, если они различны только в одном разряде.
Определение существенной и фиктивной переменной
Переменная существенная, если существует пара соседних наборов, функции от которых имеют различные значения. Переменная фиктивная, если значения функции на всех парах соседних наборах одинаковы.
Дать определение и построить таблицу для импликации, функции Шеффера, стрелки Пирса и сложения по модулю 2, конъюнкции, дизъюнкции, отрицания, эквиваленции
Конъюнкция - логическая операция, истинная только тогда, когда оба исходных высказывания истинны.
Дизъюнкция - логическая операция, ложная только тогда, когда оба исходных высказывания ложны.
Отрицание - логическая операция, ложная тогда, когда исходное высказывание истинно и наоборот.
Импликация - логическая операция, ложная только тогда, когда первое исходное высказывание истинно, а второе ложно.
Эквиваленция - логическая операция, истинная тогда, когда оба исходных высказывания одинаковы.
Сложение по модулю 2 - логическая операция, истинная только тогда, когда исходные высказывания различны.
Функция Шеффера - логическая операция, ложная тогда, когда оба исходных высказывания истинны.
Стрелка Пирса - логическая операция, истинная только тогда, когда оба исходных высказывания ложны.
|
|
|
| X | Y | Коньюн | Дизъюн | Отриц Y | Импл | Эквив | Слож | Шефф | Пирс |
Закон коммутативности, правила поглощения

Закон дистрибутивности дизъюнкции относительно конъюнкции, правила расщепления

Закон дистрибутивности конъюнкции относительно дизъюнкции, правила де Моргана
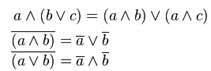
Закон ассоциативности, закон двойного отрицания

Законы с константами

Определение булевой формулы
Булева формула – логическая формула, содержащая переменные и определённые связки – конъюнкцию, дизъюнкцию и отрицание. Любая формула может быть записана в форме булевой формулы.
Правила «поглощения отрицания», представление импликации с помощью булевой формулы

Представление функции Шеффера и сложения по модулю 2 с помощью булевой формулы

Представление стрелки Пирса и эквиваленции с помощью булевой формулы

Определение противоположных наборов и двойственной функции
Противоположные наборы – наборы, все значения аргументов которых взаимно противоположны.
Двойственной для функции f(x1, x2, …, xn) называется функция

Свойства двойственных функций
А) f*(x1,...,xn)*= f(x1,...,xn)
Б) Функция, двойственная к суперпозиции функций, равна суперпозиции двойственных функций.
Если h=f(g1,..gn), то h*=f*(g1*,..gn*)
Пары двойственных функций двузначной логики
Конъюнкция и дизъюнкция, штрих Шеффера и стрелка Пирса, эквиваленция и сложение по мод 2
Определение полинома Жегалкина для функции двух и трех переменных
n=2 a0⊕a1x⊕a2y⊕a12xy a{0,1}
n=3 a0⊕a1x⊕a2y⊕a3z⊕a12xy⊕a13xz⊕a23yz⊕a123xyz
Представление основных функций полиномами Жегалкина

Определение полной конъюнкции n переменных. Определение СДНФ
|
|
|
СДНФ – функция ДНФ, которая удовлетворяет требованиям полной конъюнкции:
А) в каждой элементарной конъюнкции участвуют все n переменных
Б) каждая переменная встречается 1 раз(с отрицанием или без)
В) все элементы конъюнкции различны, нет одинаковых.
Определение полной дизъюнкции n переменных. Определение СКНФ
СКНФ – функция КНФ, которая удовлетворяет требованиям полной дизъюнкции:
А) в каждой элементарной дизъюнкции участвуют все n переменных
Б) каждая переменная встречается 1 раз(с отрицанием или без)
В) все элементы дизъюнкции различны, нет одинаковых.
|
|
|


