 |
Определение замкнутого класса. Дать определение линейной функции.
|
|
|
|
Р={f1,..,fn} является замкнутым классом, если его замыкание относительно операции суперпозиции совпадает с ним самим: [P]=P
Булева функция f(x1,...,xn) называется линейной, если существуют такие a0,a1,a2,..,an (aiÎ{0,1}), что для любых x0,x1,x2,..,xn имеет место равенство: f(x1,...,xn)=a0⊕a1x1⊕a2x2⊕..⊕anxn
Дать определение сравнимых наборов, монотонной и немонотонной функции
Альфа и бэта
Наборы являются сравнимыми, если A(a1..an), B(b1..bn) Ai<=Bi iÎ{1..n}
Функция монотонна если для всех A<B и f(A)<=f(B)
Функция не монотонна если хотя бы для одного A<B и f(A)>f(B)
22 Дать определение самодвойственной функции и функции, сохраняющей 0 и 1.
функция f(x1, x2, …, xn) является самодвойственной, если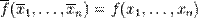 
Функция сохраняющая 0 - логическая функция, значение которой равно 0, если все аргументы равны 0: f(0,0,...,0) = 0.
Функция сохраняющая 1 - логическая функция, значение которой равно 1, если все аргументы равны 1: f(1,1,...,1) = 1.
Определение полной системы, теорема Поста
Система является полной, если множество функций, входящих в эту систему совпадает с замыканием этого множества [P]=P2.
Теорема Поста – Набор булевых функций P является полным тогда и только тогда, когда он не содержится полностью ни в одном из классов (T0,T1,L,S,M)
К-значная логика
Определение функции k-значной логики. Сколько всего функций к-значной логики от n переменных
В k- значной логике значения аргументов и значения функции могут принимать любые значения из следующего множества {0, 1, …, к-1}. Число всех функций k-значной логики от n переменных равно 
2 Определение функций ji(x), x⊃y, x÷y, Ji(x), x-y, x(отриц), -x, ~x, Vk(x,y)
Закон коммутативности и ассоциативности для функций k-значной логики. Какие функции ему удовлетворяют?
|
|
|
Коммутативность: x0y=y0x 0Î{+,*,max,min}
Ассоциативность: x0(y0z)=(x0y)0z 0Î{+,*,max,min}
Закон дистрибутивности max относительно min и min относительно max
1). Дистрибутивность функции max относительно функции min:
max [ min(x, y), z ] = min [ max(x, y), max(y, z) ].
2). Дистрибутивность функции min относительно функции max:
min [ max(x, y), z ] = max [ min(x, z), min(y, z) ].
Закон двойного отрицания. Удовлетворяет ли этому закону отрицание Поста?
Закон двойного отрицания в двузначной логике возвращает исходное значение выражению под двойным отрицанием. Закон Поста не удовлетворяет этому закону, так как он гласит x(отриц)=х+1 (mod k), х(дв.отриц)=(х+1)(отриц)(mod k)=х+2 (mod k). Чтобы вернуться к х, нужно чтобы количество операций отрицания Поста было проведено k раз.
Дать определение функций: отрицание Лукашевича и отрицания Поста. Какая из функций удовлетворяет закону двойного отрицания?
Отрицание Лукашевича ~x=(к-1)-х, удовлетворяет закону двойного отрицания, так как при двойном его применении мы вернём первоначальное значение переменной ~(~x)= ~(k-1-x)=k-1-(k-1-x)=k-k-1+1+x=x. Отрицание Поста не удовлетворяет закону двойного отрицания, так как х(дв.отриц)=(х+1)(отриц)(mod k)=х+2 (mod k).
Аналоги правил де Моргана в к-значной логике
min(~x,~y)=~max(x, y);
max(~x,~y)=~min(x, y).
Определение I формы для функции k-значной логики. Аналогом какой формы для функции 2значной логики она является?
I форма для функции k-значной логики – способ представления функции f(x1..xn), являющийся аналогом СДНФ для функций двузначной логики. f(x1..xn)=max(min(f(x1..xn),Js1(x1),Js2(x2)…Jsn(xn)),…) Где максимум берётся по всем наборам f(s1.. sn) значений переменных х1..xn
Определение II формы для функции k-значной логики. Аналогом какой формы для функции 2значной логики она является?
II форма для функции k-значной логики – способ представления функции f(x1..xn), являющийся аналогом полинома Жигалкина для функций двузначной логики. f(s1..sn)=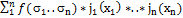 
Где суммирование ведётся по всем наборам f(s1.. sn) значений переменных х1..xn
|
|
|
|
|
|
